下载:
-
全波形反演是一种综合运用地震波场的运动学和动力学信息，通过不断匹配正演波场与实测波场来调整模型，以获得地下准确速度场的反演方法。20世纪80年代， Tarantola[1]最早提出了基于广义最小二乘法的时域波动方程波形反演；随后Pratt等[2-5]将全波形反演理论推广到频率域，形成了频率域全波形反演方法；Shin等[6]针对常规时域和频域方法无法高精度恢复速度场长波长分量等问题，提出了拉普拉斯域波形反演，并将其改进到拉普拉斯-傅里叶域。
作为目前理论最先进且精度最高的建模、成像手段，全波形反演被国内外众多学者广泛应用于海陆地震资料处理中。20世纪80年代，Gauthier等[7]和 Mora [8]最早实现了二维模拟地震数据的全波形反演，验证了理论可行性；90年代，Pratt [2]和Song等[9]利用宽角透射波信息重构速度模型，进一步发展了全波形反演方法；2004 年，Ravaut 等[10]将全波形反演应用于深部地层，实现了整个岩石圈的反演成像；2009 年，Smithyman 等[11]提出了利用大偏移距、折射信息来进行波形反演，获得了优于旅行时反演的结果；2010 年，Sirgue等[12]对挪威北海油田Valhall 地区的OBC数据进行了全波形反演，对该区的浅层低速气云进行了准确描述并对周边充气断裂构造进行了精细刻画；随后全波形反演陆续应用于海底电缆（OBC）、常规拖缆、变深度拖缆等不同采集类型的海上地震资料[13-16]。
相对于海上资料波形反演开展的如火如荼，针对陆上地震资料的波形反演研究工作比较少。2012年，Plessix等[17]利用低频、大偏移距观测系统采集了一条二维地震数据，从1.5 Hz的低频开始进行全波形反演，取得了较好的反演结果，验证了陆上资料开展全波形反演的可行性，但由于这种观测系统在实际采集中推广难度较大，因此不具有普遍性。杨勤勇等[18]分析认为陆上资料全波形反演的瓶颈在于：①全波场信息的获取严重不足。全波形反演要求全方位角、大偏移距的观测系统，而陆上地震勘探多是基于反射波勘探的滚动采集，偏移距较小、地震波传播路径正交程度差，限制了全波场信息的获取；②低频信息严重缺失。海上数据去除海洋噪声干扰后的最低可用频带为3.0～3.5 Hz，传统陆上检波器的频带有效范围为6 Hz以上；③陆地资料信噪比偏低。波形反演对噪声敏感度高，而陆地资料通常干扰波复杂，信噪比明显偏低，给数据预处理提出了较高要求，制约了全波形反演的适用性；④误差函数收敛效果差。陆上震源、检波器等不确定因素导致波动方程很难完全模拟全部波形，影响了误差函数的收敛方向。鉴于以上情况，开展陆上全波形反演相关研究的难度是较大的，需要克服从理论到算法的多重困难。
综合考虑全波形反演的适用性可以发现，其与多个方面的因素有关，如高信噪比（宽方位、大偏移距）的原始地震数据、精确的初始速度模型、准确的震源子波、精细的正演模拟算法以及高性能的计算设备等[19]。这些因素涵盖了从采集到处理、从数据到模型、从算法到硬件等多个方面。这充分说明全波形反演是一个复杂的系统工程，但其特性又展现出良好的研究潜力，如果能获得突破，全波形反演将为地球物理勘探揭开新的篇章。
-
天然气水合物是一种新型洁净能源，其作为一种潜在的煤炭石油替代品得到了广泛的研究。似海底反射（BSR）是识别天然气水合物的最直观证据之一，为了正确识别BSR，许多学者利用BSR上方（可能的水合物层）、下方（可能的游离气层）沉积层存在特殊弹性参数结构的特征，对天然气水合物及游离气的分布特征和形成机制进行了分析，同时研究了BSR上、下方的地震速度结构[20-21]。全波形反演作为一种高精度的速度建模及成像手段，在水合物的研究中发挥了重要作用。
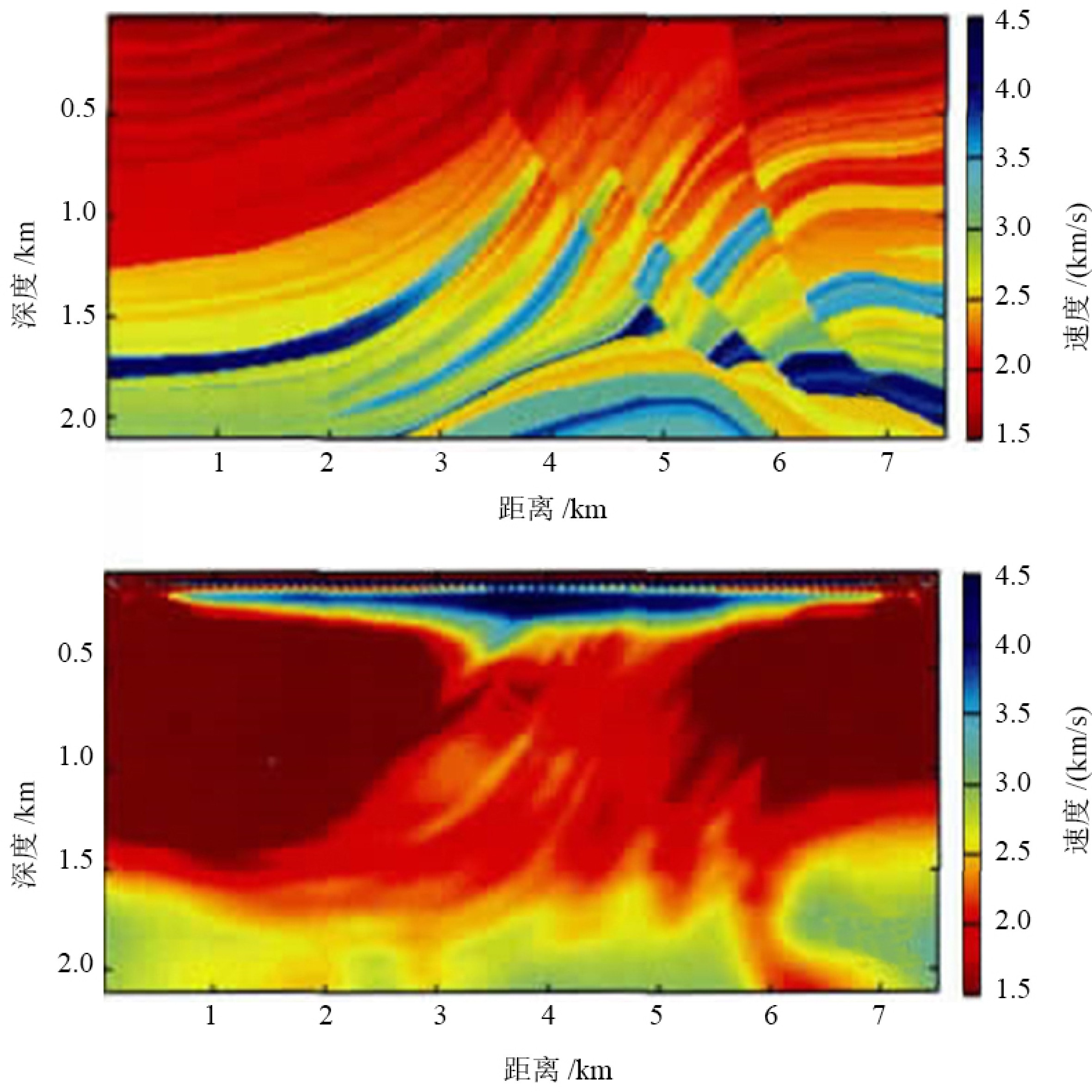
Singh等[22]于1993年首次提出了全波形反演的方法，并将这一方法应用于温哥华岸外的天然气水合物反射层速度结构的研究中。他的研究结果也被大洋钻探146航次证实，此后全波形反演的方法得到了广泛的应用和发展。Yuan等[23]在温哥华北部的Cascadia大陆边缘对多道地震数据进行了全波形反演，得到的速度结构表明：含有水合物地层的速度比不含水合物或游离气地层速度下降的更快，并估算出了水合物的浓度。Minshull等[24]提出的波形反演主要分三步，首先由均方根速度计算出主要反射层之间的层速度，然后用蒙特卡洛最大能量法获得精确的层速度，最后在频率-慢度域用共轭梯度法进行波形的拟合，取得了良好的效果。Pecher等[25]对秘鲁岸外的BSR精细速度结构进行了波形反演，并尝试了气体饱和度的估算方法。Sain等[26]对Makran大陆边缘资料进行的波形反演，揭示了海底500～800 m深度存在明显的BSR，其下的低速带表明下方沉积物中存在大量气体（图1），且此处的BSR与布莱克海台处的地震特征类似，并分析这些游离气是由于温压条件的改变造成水合物稳定带的基底上移，从而导致水合物分解而产生。Westbrook[27]对挪威Storegga 地区大陆边缘的地震资料进行了三维层析反演、二维射线追踪反演以及一维波形反演，BSR上方的速度异常揭示了水合物的存在；2012年，Jaiswal[28]等在印度Krishna-Godavari盆地进行了二维多道地震的频率域波形反演，速度模型显示有斑片状的水合物存在。
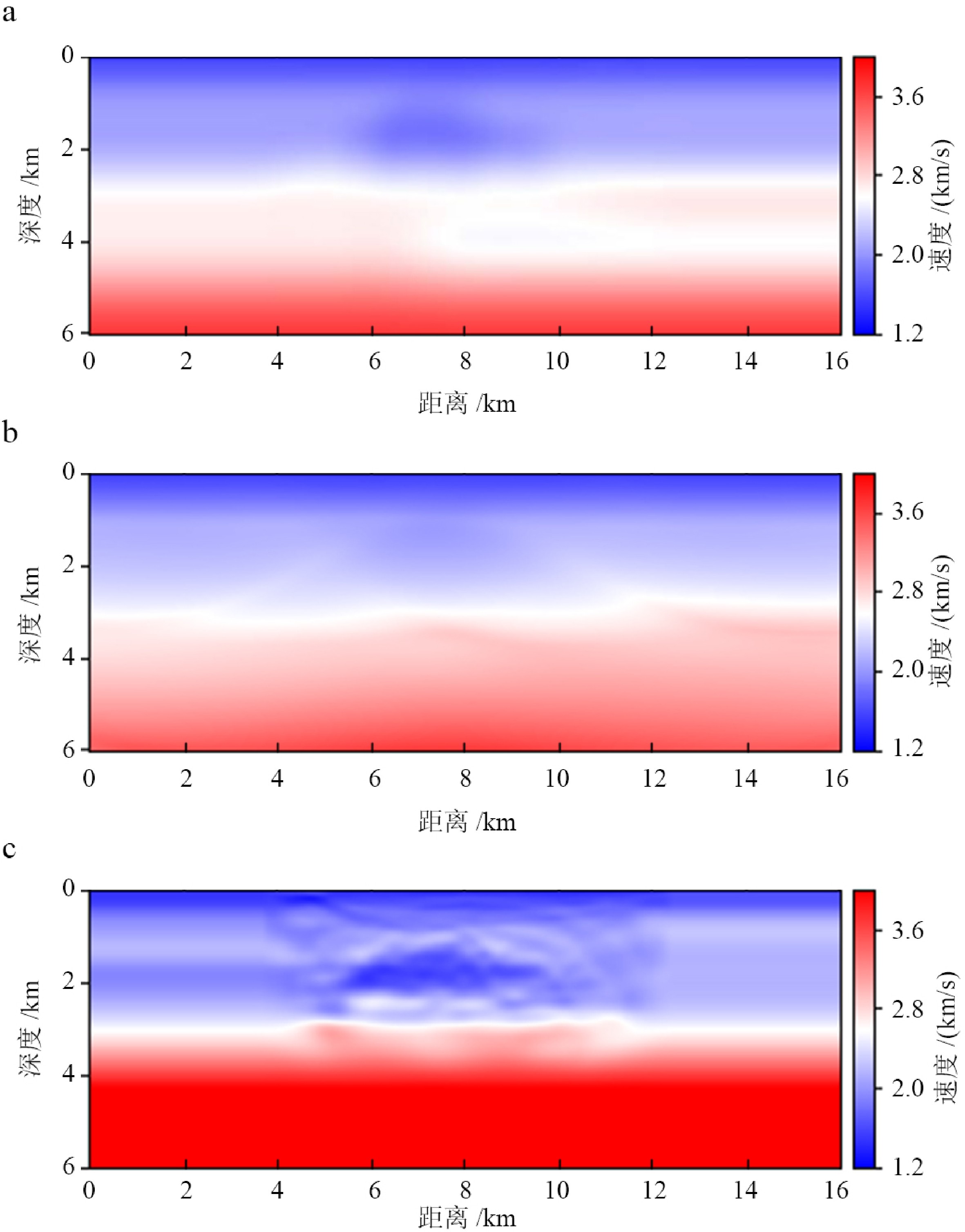
国内的天然气水合物波形反演起步较晚。宋海斌最早针对日本东南海海槽增生楔的双BSR速度结构开展了研究，提出了与Singh类似的水平层状弹性介质的截距时间-水平慢度域波形反演思路[20]，即首先根据τ-p域走时数据应用非常快速模拟退火算法求得速度结构的长波长部分，然后将第一步的速度模型作为初始模型，利用共轭梯度法求得速度的短波长扰动部分。唐勇等通过地震似海底反射层的识别，以BSR作为天然气水合物稳定带的底，通过波形反演、AVO技术来确定水合物稳定带的上界[29]，其研究的亮点在于他们还考虑了水合物稳定带的饱和度、孔隙度等一系列影响因素，来估算水合物稳定带的厚度。徐宁从理论上推导了基于遗传算法的叠前全波形反演算法，全面系统地描述了计算流程，探讨了反演中不同参数对反演收敛速度和算法稳定性的影响[30]，并基于前述算法及流程，以泥底辟型水合物为样本予以验证，同时还研究了含水合物地层的速度、流体势能、密度和波阻抗等属性特征。 霍元媛等提出了一种基于遗传算法的全波形反演方法[21]（图2），将纵波速度作为反演参数，通过模型参数编码，随机生成初始模型种群，经过遗传算法的迭代，获得了高分辨率的地层速度结构，并在中国南海的天然气水合物研究中得以应用，得到了分辨率高于常规速度分析的似海底反射层速度结构，并识别出似海底反射层的速度异常。Sun通过混合反演方法（叠前AVA反演、基于遗传算法的全波形反演及叠后反演），获取了可靠的地球物理属性参数，并基于此对水合物分解引起的海底滑坡这一现象进行了数值模拟，随后，他又从模拟结果出发研究了水合物分解形成气烟囱的过程及地震响应特征[31]。王吉亮利用 OBS 和多道地震数据，进行走时反演和全波形反演，并基于反演结果建立了墨西哥湾过 GC955 站位剖面的精细速度结构，解释了水合物和游离气的分布范围，同时他还将获得的速度结构应用于深度偏移，得到了过 GC955 站位的深度剖面，利用水道-天然堤沉积体系的空间展布，结合速度模型、钻井测井资料，刻画了水合物稳定带在区域内的平面展布[32]。刘斌对稀疏OBS数据进行了全波形反演，获得了稳定的高分辨率反演结果，能够清晰地显示出含水合物沉积层的速度异常[33]。
综合分析前人研究成果，波形反演在海域地震数据方面的研究最早，也最深入。随着海域天然气水合物研究的不断深入，波形反演方法也自然而然的与其结合，并取得了良好的发展。从波形反演的适用性和水合物的赋存特性等角度考虑，可从正演模拟与子波、反演模型及算法、预处理等几个重点方面入手，进一步提升水合物波形反演的精确度和有效性，加强波形反演方法在水合物探测及成藏模式等方面的研究。
-
地震正演模拟是对特定的地质、地球物理问题做适当的简化形成数学模型，并采用数值计算的方法获取地震响应的过程。全波形反演是根据在检波器处收集到的地震数据去模拟出地下介质模型[34]，因此，地震波正演模拟是全波形反演必不可少的前期步骤。要想兼顾地震采集方式、资料特点、算法稳定性、计算效率等多个方面，并取得高分辨率的正演模拟效果，就要选择合适的方法。
现有的正演模拟方法大致可以分为两类：以射线理论为基础的方法和以波动方程理论为基础的方法。波动方程法又可以分为波动方程的数值解法和解析算法两类。以射线理论为基础的方法主要有射线追踪法、辛几何法等；波动方程的数值解法主要有有限差分法、有限元法、傅里叶伪谱法、有限体积法、广义屏法等；解析算法主要有反射率法等。
以射线理论为基础的方法计算速度快、易于实现，但在处理横向速度变化剧烈的介质（如含水合物地层）时，稳定性明显降低，且缺少地震波的动力学信息，没有考虑全波场特征，因此不能满足全波形反演的需要。波动方程数值解法不仅能保持地震波的运动学特征，而且还能保持地震波的动力学特征，能够较为精确地模拟任意复杂介质的地震波波场，但是计算量大，计算效率较低。
Kennett提出了计算分层均匀介质所有响应的广义反射透射系数矩阵方法[35]。该方法的基本思想是首先利用Fourier-Hankel变换，将时间-空间域内的波动方程转化到频率-慢度域，然后根据实际问题求解，得到震源引起的响应，最后对该响应进行Fourier-Hankel积分反变换完成时间-空间域内介质响应的计算。随后，Kennett等进行了一系列的改进使得广义反射透射系数矩阵法的基本理论已经比较完善[36]。广义反射透射系数矩阵方法能够合成分层均匀介质的完全响应，允许反演过程中考虑调谐效应，来自多次波和转换波的干扰，以及在存在速度梯度的情况下的反射和透射效应[28]，且计算效率高，因此大部分的水合物波形反演都采用该方法进行正演计算[20-21, 37]。
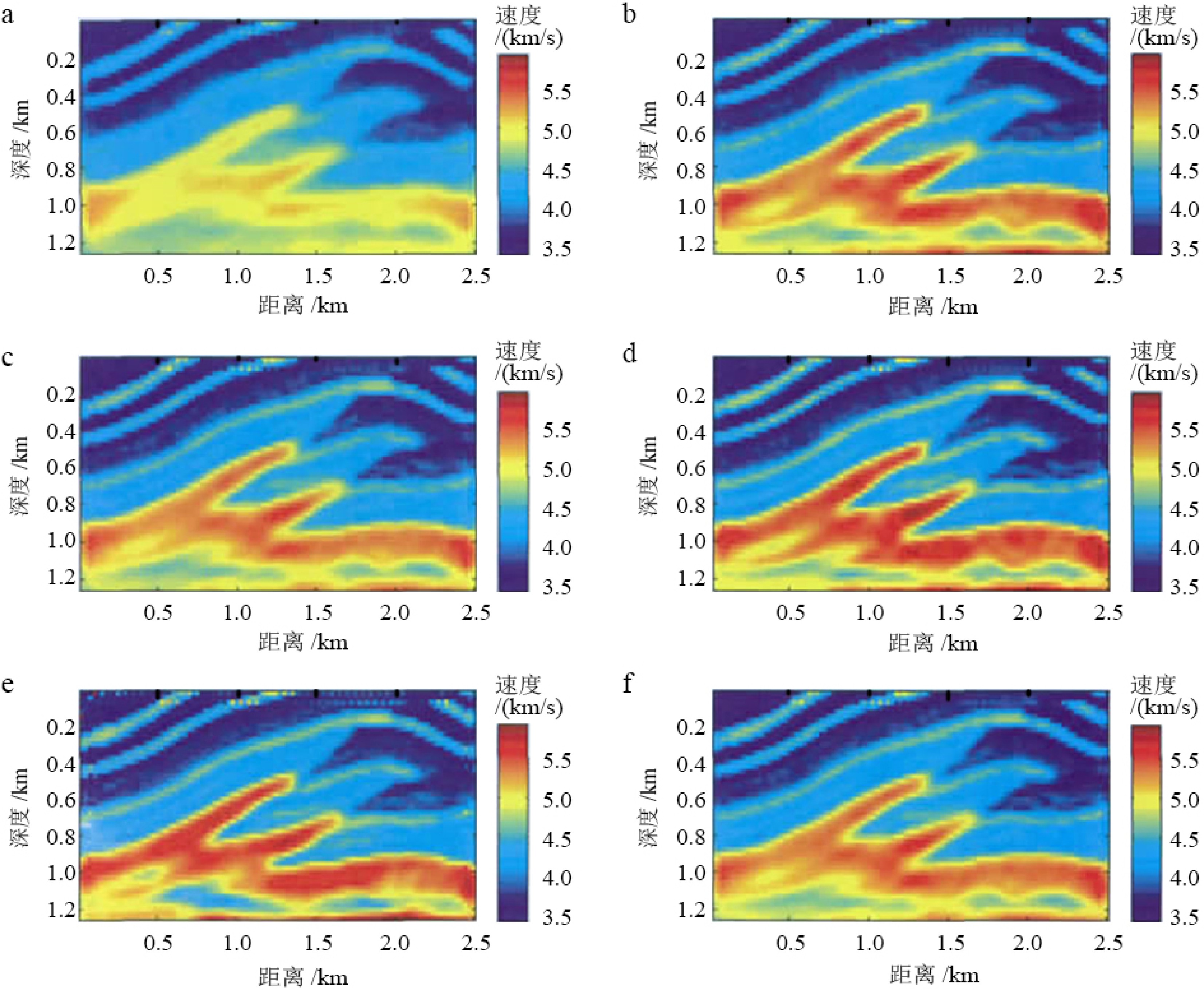
但是广义反射透射系数矩阵法只适用于垂向水平层状非均匀介质，当水合物赋存区域构造复杂时，该方法就无法准确描述波场。随着计算机性能的逐渐提高，不少学者开展了波动方程法的正演模拟相关研究。Marfurt对有限差分法和有限元法的计算结果分别在时间域和频率域进行了对比，认为在频率域有限元法的解最为精确，但是最耗机时[38]。何彦锋等从正演模拟的计算精度、计算效率、频散特性以及适用性等方面对边界元法和有限差分法进行了比较研究，认为在处理内部非均质和高频计算时，有限差分法更有效[39]。Virieux首次使用二阶交错网格有限差分方法进行波场正演模拟[40]，随后这一方法得到不断发展，目前，高阶交错网格有限差分法已经广泛应用于全波形反演。Barnes等使用轴向对称的有限差分法来正演模拟各项异性介质中的弹性波传播，对日本南海海槽的天然气水合物开展了研究[41]；Pratt等采用有限差分法对加拿大Mallik地区的水合物进行了波形反演，获得了高分辨地震速度结构[42]；Jaiswal等使用了频率域全波形反演，在印度Krishna-Godavari盆地进行了纵波速度与衰减系数反演，从而确定了天然气水合物分布范围[28]。除此以外，还有不少有代表性的正演方法涌现，如基于三维27点加权平均算子的粘声波正演法[43]、省资源有限体积法[44]、不连续的 Galer-kin方法[45]，张伟等[46]将GPU/CPU 并行计算技术应用到全波形反演中，极大地提高了计算效率。Kim等采用声波-弹性波耦合波动方程进行有限元法的正演，对日本海Ulleung盆地的天然气水合物带的特征和分布进行了调查[47]。Guasch对比了声波和弹性波模拟波场信号，认为声波全波形反演在参数合适的时候仍然可以获得较好的结果[48]。从对比图（图3）中可以明显看出弹性波波场记录比声波波场记录更复杂。尽管震源是纯炸药震源，接收器是水下检波器，但双重转换的P波和其他弹性效应为声波增加了显著的尾波，并改变了它们的 AVO 及其他振幅特性，但它们并不会影响主要纵波的旅行时。Guasch的研究也说明，在参数化合适的情况下，声波全波形反演仍然可以获得理想的反演结果。
-
能否获得准确的震源子波是全波形反演较为关键的步骤。何兵红等通过数值示例表明子波相位变化引起波形变化，会影响全波形反演的梯度计算[49]。同时子波主频也是影响全波形反演的重要因素，主频过大或过小都会引起反演结果的不准确。全波形反演对子波振幅不是特别敏感，但当振幅过大时会干扰梯度的求取。为了使振幅匹配，需要将子波和原始数据进行组合校正。 Crutchley的做法是将选定位置处一定范围内的CMP道集进行时移，使得海底波峰振幅对齐，然后将这些道集叠加；再对首个海底多次波应用同样的处理，并将其极性反转，与海底极性相同；然后将所有这些叠加后的海底子波与海底多次子波求平均，以获得最终的震源子波[50]。Xia等则认为反演过程中应同时考虑子波，而不是将子波固定[51]。还有的学者为了克服震源子波的影响，提出了不依赖于震源子波的全波形反演方法，如频率域的卷积波场和反卷积波场方法[52-58]。
敖瑞德等通过对Marmousi速度模型的数值实验，发现即使采用相对精确的高斯平滑初始模型，但使用错误的子波，常规的全波形反演仍然无法得到好的反演结果[59]（图4）。秦宁总结了获得震源子波的两类方法：一类是利用原始地震数据进行子波估计；另一类是直接从原始地震数据中反演子波，或者进行速度与子波的多参数全波形反演[60]。
子波估计的准确性，会严重影响反演过程中数据的拟合，直接决定反演成功与否。在天然气水合物的波形反演中，大多数学者都假设海底子波是震源子波和反射系数序列的褶积，并从海底反射及其首次多次波中提取震源子波[24-26]，以期获得较好的拟合结果。
-
全波形反演由Tarantola[1]最早提出，经历了时间域的多尺度反演方法、频率域全波形反演、频率迭代的多尺度全波形反演、拉普拉斯域的全波形反演等发展阶段，由时间域到频率域，再到拉普拉斯域，由海洋到陆地，由2D到3D不断进步并实用化。在这个过程中，全波形反演方法的发展曾遭遇不少障碍，其中最大的瓶颈就是实际资料中低频分量与初始速度模型的耦合问题[18]。早在1986年，Gauthier等最早对二维地震资料进行全波形反演时，就指出了全波形反演对于初始模型的严重依赖[7]。Virieux等认为受初始模型精度及低频缺失的影响，局部优化算法无法阻止目标函数向局部最小值收敛[61]。Nikhil等通过模型实例揭示了一个成功的全波形反演需要足够的低频成分和精确的初始速度模型的耦合[62]。由于全波形反演常受周波跃迁问题困扰，一个好的初始模型能够帮助波形反演跳出局部最优解的陷阱。秦宁认为初始模型的准确程度决定了全波形反演的成功与否，通过对不同初始模型进行反演，发现平滑速度模型的反演结果优于常梯度速度模型，分析其原因是速度场的低频成分需要在初始速度模型中给予准确的表达，平滑后的速度模型低频成分保留的较好，高频成分在反演迭代的过程中可以得到有效恢复，而常梯度速度模型低频成分的准确度低会使得反演无法收敛到全局最优解[60]。因此，在实际资料的应用中，一个好的初始模型是全波形反演成功的前提条件。
Virieux等总结了三种全波形反演初始模型的建立方式：初至旅行时层析成像、立体层析成像和拉普拉斯域反演[61]。
初至旅行时层析成像是指利用各种类型地震波的初至旅行时信息来反演地下介质速度。它只利用地震波的旅行时信息，数据计算量小，并且旅行时反演的非线性程度相对较弱，正演模拟和反演迭代相对稳定，因此，在实际生产中的应用最为广泛。Brenders等实现了旅行时层析与全波形的联合反演，认为旅行时层析所获得的初始模型的精度、丰富的低频成分以及大偏移距信息为全波形反演提供了重要的基础[63]。Prieux等评估了二维频率域全波形反演的敏感性，包括对采集到的最小偏移距、对自由表面效应以及对初至旅行时反演得到的初始模型和立体层析成像得到的初始模型精度等各方面影响因素[64]（图5）。评估结果表明，初至层析能够帮助波形反演得到比较好的浅层模型，而立体层析能够有效恢复速度的长波长分量。
图 5 波形反演对初始模型的灵敏度对比
Figure 5. Initial models for FWI
但是当实际资料中存在低速带时，如何拾取可靠的初至旅行时是一个难题，因此，Billette等提出了立体层析成像技术[65-69]。立体层析成像是一种基于反演数据体的旅行时间和局部相干同相轴斜率的层析成像方法，与常规旅行时反射层析成像相比，立体层析成像的最大特点是数据空间的分布可以是稀疏的、不连续的[65]，它可以半自动拾取局部相干同相轴，且更简便，拾取密度更高。这种方法除了利用地震波走时，还使用炮、检点位置与炮、检点处射线的局部传播方向来约束速度模型[66]，比传统层析成像算法更稳定。刘定进等采用高斯束层析与全波形反演进行联合速度建模，取得了较好的效果[70]。Prieux等联合折射和反射立体层析成像建立了频率域全波形反演初始模型，并应用于Valhall油田资料的全波形反演，为研究低速气层和储层下方深部构造提供了更可靠的初始模型[64]。
拉普拉斯域波形反演算法稳健并且不依赖于初始模型，能够给频率域波形反演提供一个光滑的初始速度模型，Shin等将这种波形反演与直接在频率域进行的波形反演在多种模型上进行了对比，认为将拉普拉斯域波形反演结果作为初始模型的反演结果更好[71]。虽然拉普拉斯域波形反演能够恢复模型的低频成分，但是反演深度容易受偏移距和衰减的影响，Shin等利用阻尼波场的低频分量，提出了 Laplace-Fourier波形反演算法，并将其应用于频率小于地震带宽的最小频率的资料[71]。刘张聚建立了一种基于时域加权的拉普拉斯-频率域弹性波全波形反演方法，他通过引入拉普拉斯衰减因子降低了全波形反演对于低频成分的依赖性，形成了兼具三种域优势的时间-拉普拉斯-频率域弹性波全波形反演方法[72]。
据王连坤等[73]总结，除走时层析、拉普拉斯域反演以外，偏移速度分析也是主要的初始模型建立方法。偏移速度分析是利用波场传播算子产生扩展的成像道集，并通过一定的判定准则来获取最佳偏移速度的方法[19]。其中，波场传播算子可以是动校正叠加算子、倾斜校正叠加算子，也可以是克希霍夫偏移算子、叠前时间偏移算子等；成像道集可以是角度域，也可以是地下偏移距域等；判定准则可以是道集拉平、能量聚焦或能量叠加最大化。这种方法需要在每次迭代更新速度模型后进行叠前深度偏移，因此计算成本较高，国内外学者很少利用偏移速度分析方法来构建全波形反演的初始模型，其主要还是用于偏移成像领域。
针对天然气水合物的波形反演，出于计算效率和保证算法收敛的考虑，一般都使用旅行时层析算法先获得速度模型的长波长分量，然后再用波形反演重建该模型的细节部分，得到模型的短波长分量，这样就可以得到一个比较精确的速度模型 [20-21, 24-25, 37, 50]。
-
Brossier等通过海上、陆上含噪模型数据的计算，对比了最小平方L2范数、最小绝对值L1范数、Huber 准则和混合准则等4种最小化函数在频率域波形反演中的表现[74]（图6），其中Huber 准则和混合准则是L1范数和L2范数二者的联合函数。计算结果表明，L1范数对噪音不太敏感，能提供最可靠的速度模型；L2范数在存在均匀白噪的情况下，如果能牺牲计算效率而减小频率采样间隔也能够得到可靠的结果；而Huber 准则和混合准则在转换门阀选择合理的情况下，也能够提供令人满意的结果。Liu等通过对互相关函数与L2范数等不同目标函数的对比，阐明了互相关函数作为目标函数的优势[75]。Guasch等将维纳滤波器引入目标函数，并将该方法推广到三维，在缺失低频信息的情况下获得了很好的反演结果[48]。Shin等提出利用对数波场来构建目标函数，其允许考虑三种类型的目标函数，即只有振幅、只有相位或二者皆有的目标函数，在对不同数据进行常规目标函数和对数波场目标函数的波形反演后发现，对于合成数据来说，新方法获得的速度模型要优于传统波形反演；对实际地震数据应用新方法进行反演，则能更好地揭示近地表的高频特征[71]。此后，Shin等又使用对数目标函数方法的变体即全对数方法进行全波形反演，并将结果与常规最小二乘法进行比较，发现对数反演更加稳健，分析原因可能是对数方法对残余波场的振幅产生了自然调节，其使计算稳定，从而改善反演结果[76]。Bednar等的研究认为，基于相位的对数方法比传统方法更实用[77]。Pyun等分别使用仅考虑振幅的对数波场目标函数和常规波场目标函数进行波形反演，认为后者的反演结果较好，但仍比对数波场目标函数和基于相位的对数波场目标函数的结果要差，因此不建议反演中单独使用基于振幅的对数波场目标函数[78]。廖文等提出改进算法中固定不变的目标函数，在反演过程中有针对性地调整目标函数，以达到在不增加计算量的前提下降低频率域全波形反演算法对初始模型的依赖，提高算法的适用性的目的[79]。
图 6 不同目标函数对含噪数据的纵波速度全波形反演结果
Figure 6. Reconstructed left VP and right VS models for the first Valhall test with the noisy data after the two FWI steps.
时间域的波形反演主要有两类目标函数：一类是将目标函数定义为最小化预测波场与观测波场之间的误差[51]，另一类是将目标函数定义为规则化的互相关函数[76]。最早Singh进行的全波形反演是最小化采样点间的实际地震记录和合成地震记录的差值，获得了BSR层的反射速度结构和水合物层厚度，其结果由ODP验证[22]。张宝金等引入了参数和观测数据的先验概率信息，以实际数据和正演计算数据残差的加权能量为目标函数，对中国南海北部陆坡水合物钻探区的资料进行了波形反演[80]。徐宁则认为传统的误差目标函数收敛速度较慢，而相关形式的目标函数对波形的绝对旅行时要求不是很严，并且具有一定的抗噪能力[30]，因此选择和Sen等相同的目标函数[26]，即观测数据与理论数据的相关函数。宋海斌等采用τ-p域走时计算值与观测值的均方差作为目标函数，反演了日本东南海海槽双BSR的速度结构[20]。
-
现有的地球物理反演方法主要有两大类：一类是线性反演方法，另一类是非线性反演方法。线性反演主要是指Born近似和Rytov近似这类反演方法，这种方法仅取前向小角度辐射作近似处理，忽略了前后向波长耦合及多次反射及折射效应等构造间的相互作用 [81]，因此不适用于反演叠前地震数据。非线性反演方法主要用于解决不确定性高、非线性程度高、计算规模大的优化问题。按是否具备全局搜索能力，可以进一步将非线性反演方法分为两类[82]：①基于目标函数局部微分特性的局部方法；②基于随机搜索及兼有智能性的全局方法。其中局部优化方法主要有梯度类方法，包括最速下降法、共轭梯度法等。另外，常见的还有牛顿类方法，主要包括牛顿法、拟牛顿法、高斯-牛顿法等。全局优化方法主要有蒙特卡洛法、遗传算法、模拟退火、神经网络等。
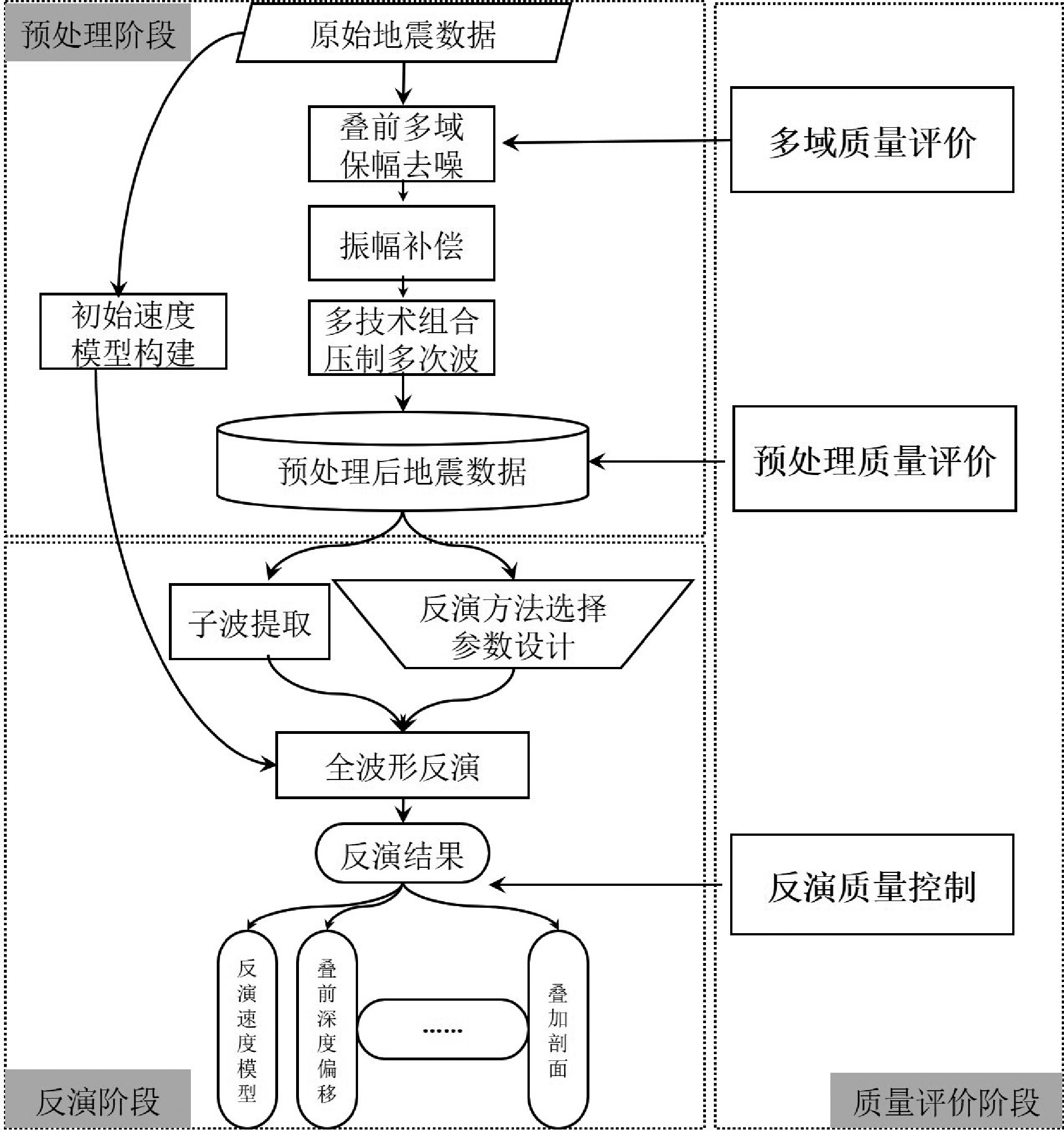
最速下降法等梯度类方法首先对梯度求解，获得目标函数的最快上升方向，然后沿负梯度方向对初始模型进行迭代更新。这种方法具有良好的全局收敛性，所需要的存储量比较小，结构简单，易于实现，Pratt等将最速下降法应用于频率域声波方程和弹性波方程的全波形反演，并对该方法进行了可靠性评估 [4]。由于梯度类算法利用的是目标函数的一阶偏导，所以其搜索过程收敛较慢。牛顿类算法不仅利用了目标函数的二阶导数，还利用了其梯度信息，因此在收敛速度上比梯度类算法更有优势[83-85]，Tarantola在将牛顿法应用到时间域全波形反演算法的过程中发现，牛顿法不仅需要计算目标函数的二阶导数，还要求海森矩阵必须满足非奇异性[1]，这也对计算提出了较高要求。高斯-牛顿法不需要对海森矩阵精确求解，因此比牛顿法的计算效率高，Hu等在进行二维多频率全波形反演时应用了此方法[86]，不但证明了方法的可靠性，还提供了可参考的工作方案。拟牛顿法则只需要计算目标函数的一阶导数，具有良好的全局收敛性和超线性收敛速度。刘璐等将该方法应用于二维频率域全波形反演，虽然成功求取了速度参数[87]，但同时也暴露出拟牛顿法的劣势，即在每次迭代过程中都需要构建逆海森矩阵，而且需要求解线性方程组来确定下降方向，存储量巨大，因此拟牛顿法只适用于中小规模问题，受此限制，直接将该方法应用于全波形反演的研究较少。共轭梯度法是利用共轭性对最速下降法进行修正来构造更好的搜索方向，既不用计算海森矩阵及其逆矩阵，又不需要目标函数的二阶导数信息，因此大大提高了收敛速度，是全波形反演最常用的方法之一。高凤霞等的研究很具有代表性，他们将几种局部优化方法应用于同一个数据的频率域二维声波方程速度参数全波形反演中（图7），从收敛速度、反演精度以及计算时间等方面进行了对比分析，认为高斯-牛顿法收敛速度最快，但稳定性稍差，最速下降法的收敛速度最慢；共轭梯度方法反演精度较高，梯度法和高斯-牛顿法的精度较低，最速下降法精度最低；最速下降方法和共轭梯度法只需计算梯度，计算用时最少[88]。
图 7 不同优化算法得到的全波形反演速度模型
Figure 7. FWI results of (a) steepest-descent method ,(b) diagonal Hessian matrix scaled method, (c) conjugate gradient method, (d) diagonal Hessian matrix scaled gradient + conjugate gradient method, (e) Gauss-Newton method and, (f) L-BFGS method [88]
局部优化方法收敛速度快，计算用时少，但反演结果强烈依赖于初始模型，对于海量的地球物理数据而言，选取一个好的初始模型绝非易事。全局优化方法不需要求导等运算，不依赖于初始模型，在解空间内随机搜索以获得全局最优解，但是其随机搜索的特征也导致算法收敛慢、时间代价高。因此如何将两者的优点结合起来是目前反演问题的一个重要研究方向。
Singh等的工作就很好地印证了这一点，他们用蒙特卡洛法来寻找全局最优解，以避免陷入局部最优解的陷阱，但其搜索方向完全随机，单参数反演时尚可，多参数同时反演时计算效率极其低下[22]。Cary等针对上述问题，提出先用蒙特卡洛法确定全局最优解的范围，然后用局部优化方法在这一范围内进一步搜索获得全局最优解[89]的思路，从反演结果来看，在指明全局优化算法的收敛方向上，该方法有不错的表现，但由于蒙特卡洛法依然是一种高算力需求的方法，在降低全局优化算法时间代价的效果方面仍比较有限。
遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局搜索优化算法[90]。Mallick提出一种基于遗传算法的全波形反演算法，应用于美国含气砂岩的研究[91]，随后Mallick等将叠前基于遗传算法的全波形反演与叠后反演相结合提出一种混合反演方法，成功用于印度安达曼海的水合物勘探[92]。徐宁建立了基于遗传算法的叠前全波形反演流程，并对算法的性能进行了分析[30]。 Huo等提出了基于遗传算法和共轭梯度法的全波形反演，用于对中国南海北部海域的天然气水合物研究[21]。另外，模拟退火法和神经网络法在全波形反演的寻优过程中也取得了很好的效果[93]。比如宋海斌等采用快速模拟退火和共轭梯度相结合的思路，先求取速度场的低频背景，再求取高频分量，对日本东南海海槽的水合物速度结构开展了研究[20]。而刘鹏程、Fallat等学者将模拟退火、神经网络与单纯形法、均匀设计等方法结合起来，有效地提高了算法的效率[94-95]。
主流的优化方法有很多，每一个方法都有其自身的优缺点及不同的适用条件。随着算法的发展，这些优化方法发展出了很多分支，也都各具特点，并不存在绝对的优劣之分。实际使用的时候，需要根据具体情况，灵活处理。在天然气水合物的全波形反演中，无论在时间域还是频率域，由于实际地震资料常常缺少低频成分，采用常规方法难以得到理想的初始模型，因此采用全局优化方法与局部优化方法相结合的混合算法，兼顾计算效率与反演精度，往往能取得高质量的反演结果。大量的实践证明，这种折衷的办法能更有效地促进全波形反演的实际应用。
-
全波形反演的预处理主要指对原始地震数据的处理，主要包括静校正、多域保幅去噪、振幅补偿、归一化处理等，其目的是为了使原始数据与正演模拟数据能够更好地匹配（图8）。由于全波形反演对数据中存在的噪声非常敏感，因此在进行反演之前做好预处理工作至关重要，既要做到最大程度地消除噪音的影响，又不能破坏波的动力学特征，实施难度很大。
图 8 预处理流程图
Figure 8. Workflow for precondition
海洋地震数据通常受多次波的影响最大，同时，受采集条件的限制，目前常规开展二维地震资料反演的最高频率通常在30 Hz以下，三维理论模型反演的最高频率在20 Hz以下，也就是说全波形反演无法恢复到全频带，从而影响了对模型的真实重现。此外，受野外采集观测系统设计的限制，原始地震资料是有限观测孔径的数据[96]，这给波形反演带来了很大困难。鉴于上述情况，如研究目的包含波形反演相关工作，在施工设计中，应酌情增加长排列、大偏移距的采集方式，将为波形反演提供丰富的低频成分，有助于反演得到较好的背景速度场，另外，宽方位采集还可以增加数据的完备性，有利于全波形反演。
-
近年来，随着原始地震数据采集质量以及超算能力的大幅提升，全波形反演逐渐由理论走向实践、从二维走向三维，尤其在天然气水合物的研究中发挥了越来越重要的作用。从大量的实践案例中可以得出结论，全波形反演作为一种高精度的速度建模及成像方法，在水合物的研究中，特别是在揭示BSR附近沉积层的地震速度、弹性参数等方面，展现出很好的适用性和优越性。同时，由于地震波传播的复杂性，全波形反演仍旧面临许多难题，如原始资料缺乏低频成分、复杂介质中地震波传播难以准确描述、震源子波估计不准、初始模型建立精度偏低、目标函数适用性不广、寻优算法性能仍待提高等。这些都严重制约了全波形反演的快速发展，因此全波形反演目前仍无法替代走时层析等传统技术。
为了解决这些难题，许多学者提出了一些很有意义的思路、方法。如董良国等认为，考虑到实际地震资料的复杂性，不一定要强求全部地震信息的匹配，可以根据不同勘探阶段对反演结果精度要求的不同，构建不同的目标函数，利用不同的地震数据子集进行波形反演，以解决全波形反演的强非线性问题[97]。至于如何构建目标函数、选择地震数据子集，取决于反演的阶段和目的，以及资料的品质、特点。王毓玮等从弹性波有限差分正演模拟出发，分析了多波多分量地震数据及其不同的数据子集随纵、横波速度，纵、横波阻抗，密度以及拉梅常数等4种弹性参数的不同空间摄动尺度的变化关系，并系统地分析了这些变化关系在不同目标函数下的变化性态，为弹性波全波形反演中目标函数的选取与反演策略的制定提供了理论指导[98]。敖瑞德等首先从理论上分析了全波形反演不依赖震源子波的可行性，提出了不依赖于子波，基于包络的全波形反演初始模型构建方法，并通过数值试验验证了其正确性[59]。胡勇等在前人的研究基础上[99-106]，提出时频域包络反演方法，从而为全波形反演的初始速度模型构建提供了一个有效途径[107]。
在天然气水合物的研究中，最初的一些全波形反演都是以纵波速度作为唯一的参数，通过经验公式求取横波速度、密度等其他参数的。这种做法虽然具有一定的理论基础，但由于缺乏对理论值和实际值的差异评估，给反演结果带来了很大的不确定性，因此利用实测数据开展多参数联合反演必然成为未来的发展趋势。Pratt等对加拿大Mallik地区的水合物层速度和Q值进行了波形反演，获得了高分辨地震速度结构[42]；Jaiswal等在印度Krishna-Godavari盆地进行了纵波速度与衰减系数的联合反演，从而确定了天然气水合物分布范围[28]。Nikhil等对挪威北海的Tommeliten Alpha野外资料实现了各向异性三维声波全波形反演，这种方法与Ratcliffe [108]的方法原则上相似，可对空间可变、倾斜的横向各向同性及各向异性介质进行反演，并且这种方法使用五参数对各向异性进行参数化[62]。这些多参数联合反演的研究为我们提供了全新的思路，可能成为未来全波形反演更广泛应用的突破口。当然值得注意的是，多参数联合反演对于反演算法的精度和稳定性提出了更高的要求。全波形反演问题本身的高度非线性化，叠加海量地震数据的超大计算规模，对于计算机硬件的超高计算性能都是巨大的挑战，需要联合多学科研究人员共同努力。
Application of full waveform inversion to gas hydrate research
More Information-
摘要: 含水合物地层的地球物理异常响应（包括似海底反射、纵波速度倒转、弹性参数异常等）是天然气水合物存在的直接证据之一，全波形反演作为一种高精度的速度建模及成像手段，也在含水合物地层的识别方面发挥了重要作用。国内外相关研究成果表明，针对含水合物地层的波形反演，涉及正演模拟方法、震源子波、初始模型、目标函数以及优化算法等多项关键技术。本文在大量文献调研的基础上，阐述了波形反演对刻画含水合物地层的技术优势，归纳总结了适用于含水合物地层的波形反演流程，为后续的研究工作提供了基础思路，同时提出多参数联合反演在未来具有广阔的应用前景。Abstract: The geophysical responses to the hydrate bearing formations, such as BSR, velocity reversion of P wave, elastic parameter anomalies, etc. are indicators of the existence of gas hydrates. Full waveform inversion used as a high-precision velocity modeling and imaging method, also played an important role in the identification of hydrate bearing formations. Relevant research results suggest that the waveform inversion of hydrate bearing formations involves a number of key techniques, such as forward simulation methods, source wavelets, initial models, objective functions, and optimization algorithms. Based on the investigations of literatures, this paper expounded the technical advantages of waveform inversion for characterizing hydrate bearing formations, summarized the waveform inversion process suitable for hydrate bearing formations, and provided some basic ideas for subsequent research. It is proposed that multi-parameter inversion has broad application prospects in the future.
-
Key words:
- gas hydrate /
- full waveform inversion /
- wavelet estimation /
- initial model /
- forward modeling
-
图 7 不同优化算法得到的全波形反演速度模型
a. 最速下降法，b. 对角海森尺度化方法，c. 共轭梯度法，d. 对角海森+共轭梯度法，e. 高斯-牛顿法，f. L-BFGS方法[88]。
Figure 7. FWI results of (a) steepest-descent method ,(b) diagonal Hessian matrix scaled method, (c) conjugate gradient method, (d) diagonal Hessian matrix scaled gradient + conjugate gradient method, (e) Gauss-Newton method and, (f) L-BFGS method [88]
-
[1] Tarantola A. Inversion of seismic reflection data in the Acoustic approximation [J]. Geophysics, 1984, 49(8): 1259-1266. doi: 10.1190/1.1441754 [2] Pratt R G, Worthington M H. Inverse theory applied to Multi-source cross-hole tomography. Part 1: Acoustic wave-Equation method [J]. Geophysical Prospecting, 1990, 38(3): 287-310. doi: 10.1111/j.1365-2478.1990.tb01846.x [3] Pratt R G, Shin C, Hicks G J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion [J]. Geophysical Journal International, 1998, 133(2): 341-362. doi: 10.1046/j.1365-246X.1998.00498.x [4] Pratt R G. Seismic waveform inversion in the frequency Domain, Part 1: Theory and verification in a physical scale Model [J]. Geophysics, 1999, 64(3): 888-901. doi: 10.1190/1.1444597 [5] Pratt R G, Shipp R M. Seismic waveform inversion in the Frequency domain, Part 2: Fault delineation in sediments using crosshole data [J]. Geophysics, 1999, 64(3): 902-914. doi: 10.1190/1.1444598 [6] Shin C, Cha Y H. Waveform inversion in the Laplace domain [J]. Geophysical Journal International, 2008, 173(3): 922-931. doi: 10.1111/j.1365-246X.2008.03768.x [7] Gauthier O, Virieux J, Tarantola A. Two-dimensional nonlinear inversion of seismic waveforms: numerical Results [J]. Geophysics, 1986, 51(7): 1387-1403. doi: 10.1190/1.1442188 [8] Mora P. Nonlinear two-dimensional elastic inversion of multioffset seismic data [J]. Geophysics, 1987, 52(9): 1211-1228. doi: 10.1190/1.1442384 [9] Song Z M, Williamson P R, Pratt R G. Frequency-domain Acoustic-wave modeling and inversion of crosshole data; Part II, Inversion method, Synthetic experiments and real-data results [J]. Geophysics, 1995, 60(3): 796-809. doi: 10.1190/1.1443818 [10] Ravaut C, Operto S, Improta L, et al. Multiscale imaging of complex structures from multifold wide-aperture seismic data by frequency-domain full-waveform tomography: application to a thrust belt [J]. Geophysical Journal International, 2004, 159(3): 1032-1056. doi: 10.1111/j.1365-246X.2004.02442.x [11] Smithyman B, Pratt R G, Hayles J, et al. Detecting near-surface objects with seismic waveform tomography [J]. Geophysics, 2009, 74(6): WCC119-WCC127. doi: 10.1190/1.3223313 [12] Sirgue L, Barkved O I, Dellinger J, et al. Thematic Set: Full waveform inversion: the next leap forward in imaging at Valhall [J]. First Break, 2010, 28(4): 65-70. [13] Prieux V, Brossier R, Kommendal J R, et al. Application of 2D acoustic frequency-domain full-waveform inversion to OBC wide-aperture data from the Valhall field[C]//The 2010 SEG Annual Meeting. Denver, Colorado: Society of Exploration Geophysicists, 2010: 920-924. [14] Ratcliffe A, Win C, Vinje V, et al. Full waveform inversion: a North Sea OBC case study[C]//Proceedings of the 81st Annual International Meeting. Society of Exploration Geophysicists, 2011: 2384-2388. [15] Takougang E M T, Calvert A J. Application of waveform tomography to marine seismic reflection data from the Queen Charlotte Basin of western Canada [J]. Geophysics, 2011, 76(2): B55-B70. doi: 10.1190/1.3553478 [16] 韩淼. 深水区地震全波形反演策略与应用[D]. 吉林大学博士学位论文, 2014. HAN Miao. Method and application of full waveform inversion for abyssal seismic data[D]. Doctor Dissertation of Jilin University, 2014. [17] Plessix R É, Baeten G, De Maag J W, et al. Full waveform inversion and distance separated simultaneous sweeping: a study with a land seismic data set [J]. Geophysical Prospecting, 2012, 60(4): 733-747. doi: 10.1111/j.1365-2478.2011.01036.x [18] 杨勤勇, 胡光辉, 王立歆. 全波形反演研究现状及发展趋势[J]. 石油物探, 2014, 53(1):77-83 doi: 10.3969/j.issn.1000-1441.2014.01.011 YANG Qinyong, HU Guanghui, WANG Lixin. Research status and development trend of full waveform inversion [J]. Geophysical Prospecting for Petroleum, 2014, 53(1): 77-83. doi: 10.3969/j.issn.1000-1441.2014.01.011 [19] 任浩然, 王华忠, 黄光辉. 地震波反演成像方法的理论分析与对比[J]. 岩性油气藏, 2012, 24(5):12-17 doi: 10.3969/j.issn.1673-8926.2012.05.002 REN Haoran, WANG Huazhong, HUANG Guanghui. Theoretical analysis and comparison of seismic wave inversion and imaging methods [J]. Lithologic Reservoirs, 2012, 24(5): 12-17. doi: 10.3969/j.issn.1673-8926.2012.05.002 [20] 宋海斌, OSAMU M, SHIN’ICHI M. 天然气水合物似海底反射层的全波形反演[J]. 地球物理学报, 2003, 46(1):42-46 doi: 10.3321/j.issn:0001-5733.2003.01.007 SONG Haibin, OSAMU M, SHIN’ICHI M. Full waveform inversion of gas hydrate-related bottom simulating reflectors [J]. Chinese Journal of Geophysics, 2003, 46(1): 42-46. doi: 10.3321/j.issn:0001-5733.2003.01.007 [21] 霍元媛, 张明. 基于遗传算法的天然气水合物似海底反射层速度结构全波形反演[J]. 石油地球物理勘探, 2010, 45(1):55-59 HUO Yuanyuan, ZHANG Ming. The genetic algorithm based velocity structure waveform inversion for gas hydrate bottom simulating Reflection (BSR) [J]. Oil Geophysical Prospecting, 2010, 45(1): 55-59. [22] Singh S C, Minshull T A, Spence G D. Velocity structure of a gas hydrate reflector [J]. Science, 1993, 260(5105): 204-207. doi: 10.1126/science.260.5105.204 [23] Yuan T, Spence G D, Hyndman R D, et al. Seismic velocity studies of a gas hydrate bottom-simulating reflector on the northern Cascadia continental margin: amplitude modeling and full waveform inversion [J]. Journal of Geophysical Research:Solid Earth, 1999, 104(B1): 1179-1191. doi: 10.1029/1998JB900020 [24] Minshull T A, Singh S C, Westbrook G K. Seismic velocity structure at a gas hydrate reflector, offshore western Colombia, from full waveform inversion [J]. Journal of Geophysical Research:Solid Earth, 1994, 99(B3): 4715-4734. doi: 10.1029/93JB03282 [25] Pecher I A, Minshull T A, Singh S C, et al. Velocity structure of a bottom simulating reflector offshore Peru: Results from full waveform inversion [J]. Earth and Planetary Science Letters, 1996, 139(3-4): 459-469. doi: 10.1016/0012-821X(95)00242-5 [26] Sain K, Minshull T A, Singh S C, et al. Evidence for a thick free gas layer beneath the bottom simulating reflector in the Makran accretionary prism [J]. Marine Geology, 2000, 164(1-2): 3-12. doi: 10.1016/S0025-3227(99)00122-X [27] Westbrook G K, Chand S, Rossi G, et al. Estimation of gas hydrate concentration from multi-component seismic data at sites on the continental margins of NW Svalbard and the Storegga region of Norway [J]. Marine and Petroleum Geology, 2008, 25(8): 744-758. doi: 10.1016/j.marpetgeo.2008.02.003 [28] Jaiswal P, Dewangan P, Ramprasad T, et al. Seismic characterization of hydrates in faulted, fine-grained sediments of Krishna-Godavari Basin: Full waveform inversion [J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B10): B10305. [29] 唐勇, 方银霞, 高金耀, 等. 冲绳海槽天然气水合物稳定带特征及资源量评价[J]. 海洋地质与第四纪地质, 2005, 25(4):80-84 TANG Yong, FANG Yinxia, GAO Jinyao, et al. Characteristics of gas hydrate stability zone and evaluation of resources in Okinawa trough [J]. Marine Geology & Quaternary Geology, 2005, 25(4): 80-84. [30] 徐宁, 吴时国, 王秀娟, 等. 东海冲绳海槽陆坡天然气水合物的地震学研究[J]. 地球物理学进展, 2006, 21(2):564-571 doi: 10.3969/j.issn.1004-2903.2006.02.036 XU Ning, WU Shiguo, WANG Xiujuan, et al. Seismic study of the Gas hydrate in the continental slope of the Okinawa trough, east China sea [J]. Progress in Geophysics, 2006, 21(2): 564-571. doi: 10.3969/j.issn.1004-2903.2006.02.036 [31] Sun Y B, Wu S G, Dong D D, et al. Gas hydrates associated with gas chimneys in fine-grained sediments of the northern South China Sea [J]. Marine Geology, 2012, 311-314: 32-40. doi: 10.1016/j.margeo.2012.04.003 [32] Wang J L. Study on geophysical characterization of concentrated gas hydrate reservoirs[D]. Doctor Dissertation of University of Chinese Academy of Science, 2015. [33] 刘斌, 张衡. 海底水合物OBS数据全波形反演数值例子[J]. 地球物理学进展, 2018, 33(1):379-384 doi: 10.6038/pg2018AA0580 LIU Bin, ZHANG Heng. Full waveform inversion of OBS data from ocean gas hydrate: synthetic example [J]. Progress in Geophysics, 2018, 33(1): 379-384. doi: 10.6038/pg2018AA0580 [34] 章婷. 复杂介质地震波波场正演模拟方法研究[D]. 电子科技大学, 2014. ZHANG Ting. Research on forward simulation methods of seismic wave fields in complex mediums[D]. Master Dissertation of University of Electronic Science and Technology of China, 2014. [35] Kennett B L N. Theoretical reflection seismograms for elastic media [J]. Geophysical Prospecting, 1979, 27(2): 301-321. doi: 10.1111/j.1365-2478.1979.tb00972.x [36] Kennett B L N. Seismic waves in a stratified half space-II. Theoretical seismograms [J]. Geophysical Journal International, 1980, 61(1): 1-10. doi: 10.1111/j.1365-246X.1980.tb04299.x [37] Singh S C, Royle G, Sears T, et al. Elastic (Visco) Full Waveform Inversion of multi-component marine seismic data in the time domain: A tribute to Albert Tarantola[C]//72nd EAGE Conference & Exhibition Incorporating SPE EUROPEC 2010: Barcelona: SPE, 2010. [38] Marfurt K J. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations [J]. Geophysics, 1984, 49(5): 533-549. doi: 10.1190/1.1441689 [39] 何彦锋, 孙伟家, 符力耘. 复杂介质地震波传播模拟中边界元法与有限差分法的比较研究[J]. 地球物理学进展, 2013, 28(2):664-678 doi: 10.6038/pg20130215 HE Yanfeng, SUN Weijia, FU Liyun. Comparison of boundary element method and finite-difference method for simulating seismic wave propagation in complex media [J]. Progress in Geophysics, 2013, 28(2): 664-678. doi: 10.6038/pg20130215 [40] Virieux J. SH-wave propagation in heterogeneous media: Velocity-stress finite-difference method [J]. Geophysics, 1984, 49(11): 1933-1942. doi: 10.1190/1.1441605 [41] Barnes C, Noble M. Feasibility study to quantify gas hydrates Using an anisotropic full waveform inversion in the time domain[C]//2007 SEG Annual Meeting. San Antonio, Texas: SEG, 2007: 1825-1829. [42] Pratt R U, Bauer K, Weber M. Crosshole waveform tomography velocity and attenuation images of arctic gas hydrates[C]//73th Annual Meeting. Dallas, Texas: Society of Exploration Geophysicists, 2003: 2255-2258. [43] Operto S, Virieux J, Amestoy P, et al. 3D finite-difference frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver: a feasibility study [J]. Geophysics, 2007, 72(5): SM195-SM211. doi: 10.1190/1.2759835 [44] Brossier R, Operto S, Virieux J. Two-dimensional seismic imaging of the Valhall model from synthetic OBC data by frequency domain elastic full-waveform inversion[C]//2009 SEG Annual Meeting. Houston, Texas: SEG, 2009, 28: 2293-2297. [45] Etienne V, Chaljub E, Virieux J, et al. An hp-adaptive discontinuous Galerkin finite-element method for 3-D elastic wave modelling [J]. Geophysical Journal International, 2010, 183(2): 941-962. doi: 10.1111/j.1365-246X.2010.04764.x [46] 张伟, 彭真明, 章婷. 全波形反演中的GPU/CPU协同计算[C]//中国地球物理2013: 第十八专题论文集. 昆明: 中国地球物理学会, 2013: 350. ZHANG Wei, PENG Zhenming, ZHANG Ting. GPU/CPU collaborative computing in full waveform inversion[C]//The 29th Annual Academic Conference of the Chinese Geophysical Society. Kunming: China Geophysical Society, 2013: 350. [47] Kim Y, Shin C, Calandra H. 3D Hybrid Waveform Inversion with GPU devices[C]//2012 SEG Annual Meeting. Las Vegas, Nevada: Society of Exploration Geophysicists, 2012. [48] Guasch L. 3D elastic full-waveform inversion[D]. Doctor Dissertation of Imperial College London, 2012. [49] 何兵红, 吴国忱. 时间域全波形反演方法研究[C]//中国地球物理学会第二十八届年会论文集. 北京: 中国地球物理学会, 2012: 558. HE Binghong, WU Guochen. Study of full waveform inversion in time domain[C]//The 28th Annual Academic Conference of the Chinese Geophysical Society. Beijing: China Geophysical Society, 2012: 558. [50] Crutchley G J, Gorman A R, Pecher I A, et al. Geological controls on focused fluid flow through the gas hydrate stability zone on the southern Hikurangi Margin of New Zealand, evidenced from multi-channel seismic data [J]. Marine and Petroleum Geology, 2011, 28(10): 1915-1931. doi: 10.1016/j.marpetgeo.2010.12.005 [51] Xia G Y, Sen M K, Stoffa P L. 1-D elastic waveform inversion: A divide-and-conquer approach [J]. Geophysics, 1998, 63(5): 1670-1684. doi: 10.1190/1.1444463 [52] Lee K H, Kim H J. Source-independent full-waveform Inversion of seismic data [J]. Geophysics, 2003, 68(6): 2010-2015. doi: 10.1190/1.1635054 [53] Zhou B, Greenhalgh S A. Crosshole seismic inversion with Normalized full-waveform amplitude data [J]. Geophysics, 2003, 68(4): 1320-1330. doi: 10.1190/1.1598125 [54] Choi Y, Alkhalifah T. Source-independent time-domain Waveform inversion using convolved wavefields: Application to The encoded multisource waveform inversion [J]. Geophysics, 2011, 76(5): R125-R134. doi: 10.1190/geo2010-0210.1 [55] Choi Y, Shin C, Min D J, et al. Efficient calculation of the Steepest descent direction for source-independent seismic Waveform inversion: An amplitude approach [J]. Journal of Computational Physics, 2005, 288(2): 455-468. [56] Cheong S, Pyun S, Shin C. Two efficient steepest-descent Algorithms for source signature-free waveform inversion [J]. The Journal of Seismic Exploration, 2006, 14(4): 335-348. [57] Xu K, Greenhalgh S A, Wang M Y. Comparison of source-independent methods of elastic waveform inversion [J]. Geophysics, 2006, 71(6): R91-R100. doi: 10.1190/1.2356256 [58] Tran K T, McVay M. Site characterization using Gauss-Newton inversion of 2-D full seismic waveform in the time domain [J]. Soil Dynamics and Earthquake Engineering, 2012, 43: 16-24. doi: 10.1016/j.soildyn.2012.07.004 [59] 敖瑞德, 董良国, 迟本鑫. 不依赖子波、基于包络的FWI初始模型建立方法研究[J]. 地球物理学报, 2015, 58(6):1998-2010 doi: 10.6038/cjg20150615 AO Ruide, DONG Liangguo, CHI Benxin. Source-independent envelope-based FWI to build an initial model [J]. Chinese Journal of Geophysics, 2015, 58(6): 1998-2010. doi: 10.6038/cjg20150615 [60] 秦宁, 王延光, 杨晓东, 等. 时域全波形反演影响因素分析及井数据约束探索[J]. 地球物理学进展, 2015, 30(1):210-216 doi: 10.6038/pg20150132 QIN Ning, WANG Yanguang, YANG Xiaodong, et al. Analysis of influencing factors and exploration of well constrained for full waveform inversion in time domain [J]. Progress in Geophysics, 2015, 30(1): 210-216. doi: 10.6038/pg20150132 [61] Virieux J, Operto S. An overview of Full-waveform Inversion in exploration geophysics [J]. Geophysics, 2009, 74(6): WCC1-WCC26. doi: 10.1190/1.3238367 [62] Shah N, Warner M, Nangoo T, et al. Quality assured full-waveform inversion: Ensuring starting model adequacy[C]//2012 SEG Annual Meeting. Las Vegas, Nevada: SEG, 2012. [63] Brenders A J, Pratt R G. Full waveform tomography for lithospheric imaging: Results from a blind test in a realistic crustal model [J]. Geophysical Journal International, 2006, 168(1): 133-151. [64] Prieux V, Operto S, Brossier R, et al. Application of acoustic full waveform inversion to the synthetic Valhall velocity model[C]//2009 SEG Annual Meeting. Houston, Texas: SEG, 2009: 2268-2272. [65] Billette F, Lambaré G. Velocity macro-model estimation from seismic reflection data by stereotomography [J]. Geophysical Journal International, 1998, 135(2): 671-690. doi: 10.1046/j.1365-246X.1998.00632.x [66] Billette F, Le Bégat S, Podvin P, et al. Practical aspects and applications of 2D stereotomography [J]. Geophysics, 2003, 68(3): 1008-1021. doi: 10.1190/1.1581072 [67] 李振伟, 杨锴, 倪瑶, 等. 基于立体层析反演的偏移速度建模应用研究[J]. 石油物探, 2014, 53(4):444-452 doi: 10.3969/j.issn.1000-1441.2014.04.010 LI Zhenwei, YANG Kai, NI Yao, et al. Migration velocity analysis with stereo-tomography inversion [J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 444-452. doi: 10.3969/j.issn.1000-1441.2014.04.010 [68] 倪瑶, 杨锴, 陈宝书. 立体层析反演方法理论分析与应用测试[J]. 石油物探, 2013, 52(2):121-130 doi: 10.3969/j.issn.1000-1441.2013.02.002 NI Yao, YANG Kai, CHEN Baoshu. Stereotomography inversion method: theory and application testing [J]. Geophysical Prospecting for Petroleum, 2013, 52(2): 121-130. doi: 10.3969/j.issn.1000-1441.2013.02.002 [69] Prieux V, Lambaré G, Operto S, et al. Building starting models for full waveform inversion from wide-aperture data by stereotomography [J]. Geophysical Prospecting, 2013, 61(S1): 109-137. [70] 刘定进, 胡光辉, 蔡杰雄, 等. 高斯束层析与全波形反演联合速度建模[J]. 石油地球物理勘探, 2019, 54(5):1046-1056 LIU Dingjin, HU Guanghui, CAI Jixing, et al. A joint velocity model building method with Gaussian beam tomography and full waveform inversion for land seismic data [J]. Oil Geophysical Prospecting, 2019, 54(5): 1046-1056. [71] Shin C, Min D J. Waveform inversion using a logarithmic wavefield [J]. Geophysics, 2006, 71(3): R31-R42. doi: 10.1190/1.2194523 [72] 刘张聚, 童思友, 方云峰, 等. 基于时域加权的拉普拉斯—频率域弹性波全波形反演[J]. 石油地球物理勘探, 2021, 1,56(2):302-312, 331 LIU Zhangju, TONG Siyou, FANG Yunfeng, et al. Full elastic waveform inversion in Laplace-Fourier domain based on time domain weighting [J]. Oil Geophysical Prospecting, 2021, 1,56(2): 302-312, 331. [73] 王连坤, 方伍宝, 段心标, 等. 全波形反演初始模型建立策略研究综述[J]. 地球物理学进展, 2016, 31(4):1678-1687 doi: 10.6038/pg20160436 WANC Liankun, FANG Wubao, DUAN Xinbiao, et al. Review of full waveform inversion initial model building strategy [J]. Progress in Geophysics, 2016, 31(4): 1678-1687. doi: 10.6038/pg20160436 [74] Brossier R, Operto S, Virieux J. Which data residual norm for robust elastic frequency-domain Full Waveform Inversion? [J]. Geophysics, 2010, 75(3): R37-R46. doi: 10.1190/1.3379323 [75] Liu Y S, Ting J W, Xu T, et al. Robust time-domain full waveform inversion with normalized zero-lag cross-correlation objective function [J]. Geophysical Journal International, 2016, 209(1): 106-122. [76] Shin C, Pyun S, Bednar J B. Comparison of waveform inversion, Part 1: Conventional wavefield vs logarithmic wavefield [J]. Geophysical Prospecting, 2007, 55(4): 449-464. doi: 10.1111/j.1365-2478.2007.00617.x [77] Bednar J B, Shin C, Pyun S. Comparison of waveform inversion, Part 2: Phase approach [J]. Geophysical Prospecting, 2007, 55(4): 465-475. doi: 10.1111/j.1365-2478.2007.00618.x [78] Pyun S, Shin C, Bednar J B. Comparison of waveform inversion, Part 3: Amplitude approach [J]. Geophysical Prospecting, 2007, 55(4): 477-485. doi: 10.1111/j.1365-2478.2007.00619.x [79] 廖文, 杨艳, 张东. 基于改进目标函数的频率域全波形反演研究[J]. 科技通报, 2016, 32(4):1-5 doi: 10.3969/j.issn.1001-7119.2016.04.001 LIAO Wen, YANG Yan, ZHANG Dong. Frequency-domain Full waveform inversion algorithm based on improved objective function [J]. Bulletin of Science and Technology, 2016, 32(4): 1-5. doi: 10.3969/j.issn.1001-7119.2016.04.001 [80] 张宝金, 张光学, 耿建华, 等. 南海含天然气水合物地层速度反演方法探讨[J]. 南海海洋地质, 2008(1):78-85 ZHANG Baojin, ZHANG Guangxue, GENG Jianhua, et al. Discuss on the methods of velocity inversion of the stratum containing gas hydrates in South China Sea [J]. Geological Research of South China Sea, 2008(1): 78-85. [81] Kormendi F, Dietrich M. Nonlinear waveform inversion of plane-wave seismograms in stratified elastic media [J]. Geophysics, 1991, 56(5): 664-674. doi: 10.1190/1.1443083 [82] 杨文采. 非线性波动方程地震反演的方法原理及问题[J]. 地球物理学进展, 1992, 7(1):9-19 YANG Wencai. Methods and problems in seismic inversion of nonlinear wave equations [J]. Progress in Geophysics, 1992, 7(1): 9-19. [83] 孙为涛, 董渊. 波动方程反演的全局优化方法研究[J]. 地球物理学进展, 2007, 22(3): 797-803 SUN Weitao, DONG Yuan. Study on global optimization methods for wave equation inversion problems[J]. Progress in Geophysics, 22(3): 797-803. [84] 苗永康. 基于L-BFGS算法的时间域全波形反演[J]. 石油地球物理勘探, 2015, 50(3):469-474 MIAO Yongkang. Full waveform inversion in time domain based on limited-memory BFGS algorithm [J]. Oil Geophysical Prospecting, 2015, 50(3): 469-474. [85] 陈禹. 共轭梯度法的收敛性研究[D]. 长江大学硕士学位论文, 2011. CHEN Yu. The convergence research on conjugate gradient method[D]. Master Dissertation of Yangtze University, 2011. [86] HU W Y, ABUBAKAR A, HABASHY T M. Simultaneous multifrequency inversion of full-waveform seismic data [J]. Geophysics, 2009, 74(2): R1-R14. doi: 10.1190/1.3073002 [87] 刘璐, 刘洪, 张衡, 等. 基于修正拟牛顿公式的全波形反演[J]. 地球物理学报, 2013, 56(7):2447-2451 doi: 10.6038/cjg20130730 LIU Lu, LIU Hong, ZHANG Heng, et al. Full waveform inversion based on modified quasi-Newton equation [J]. Chinese Journal of Geophysics, 2013, 56(7): 2447-2451. doi: 10.6038/cjg20130730 [88] 高凤霞, 刘财, 冯晅, 等. 几种优化方法在频率域全波形反演中的应用效果及对比分析研究[J]. 地球物理学进展, 2013, 28(4):2060-2068 doi: 10.6038/pg20130450 GAO Fengxia, LIU Cai, FENG Xuan, et al. Comparisons and analyses of several optimization methods in the application of frequency-domain full waveform inversion [J]. Progress in Geophysics, 2013, 28(4): 2060-2068. doi: 10.6038/pg20130450 [89] Cary P W, Chapman C H. Automatic 1-D waveform inversion of marine seismic refraction data [J]. Geophysical Journal International, 1988, 93(3): 527-546. doi: 10.1111/j.1365-246X.1988.tb03879.x [90] Holland J H. Adaptation in Natural and Artificial System[M]. Ann Arbor: University of Michigan Press, 1975. [91] Mallick S. Some practical aspects of prestack waveform inversion using a genetic algorithm: An example from the east Texas Woodbine gas sand [J]. Geophysics, 1999, 64(2): 326-336. doi: 10.1190/1.1444538 [92] Mallick S, Huang X R, Lauve J, et al. Hybrid seismic inversion: A reconnaissance tool for deepwater exploration [J]. The Leading Edge, 2000, 19(11): 1230-1237. doi: 10.1190/1.1438512 [93] Ingber L. Very fast simulated re-annealing [J]. Mathematical and Computer Modelling, 1989, 12(8): 967-973. doi: 10.1016/0895-7177(89)90202-1 [94] 刘鹏程, 纪晨. 改进的模拟退火-单纯形综合反演方法[J]. 地球物理学报, 1995, 38(2):200-204 LIU Pengcheng, JI Chen. An improved simulated annealing downhill simplex hybrid global inverse algorithm [J]. Acta Geophysica Sinica, 1995, 38(2): 200-204. [95] Fallat M R, Dosso S E. Geoacoustic inversion via local, global, and hybrid algorithms [J]. The Journal of the Acoustical Society of America, 1999, 105(6): 3219-3230. doi: 10.1121/1.424651 [96] 陈章. 叠前全波形反演方法研究[D]. 电子科技大学硕士学位论文, 2012, [CHEN Zhang. Study of Full Waveform Inversion[D]. Master Dissertation of University of Electronic Science and Technology of China, 2012. ] [97] 董良国, 黄超, 迟本鑫, 等. 基于地震数据子集的波形反演思路、方法与应用[J]. 地球物理学报, 2015, 58(10):3735-3745 doi: 10.6038/cjg20151024 DONG Liangguo, HUANG Chao, CHI Benxin, et al. Strategy and application of waveform inversion based on seismic data subset [J]. Chinese Journal of Geophysics, 2015, 58(10): 3735-3745. doi: 10.6038/cjg20151024 [98] 王毓玮, 董良国, 黄超, 等. 弹性波全波形反演目标函数性态与反演策略[J]. 石油物探, 2016, 55(1):123-132,141 doi: 10.3969/j.issn.1000-1441.2016.01.016 WANG Yuwei, DONG Liangguo, HUANG Chao, et al. Objective function behavior and inversion strategy in elastic full-waveform inversion [J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 123-132,141. doi: 10.3969/j.issn.1000-1441.2016.01.016 [99] 崔栋, 张研, 胡英, 等. 近地表速度建模方法综述[J]. 地球物理学进展, 2014, 29(6):2635-2641 doi: 10.6038/pg20140625 CUI Dong, ZHANG Yan, HU Ying, et al. The review of near surface velocity modeling [J]. Progress in Geophysics, 2014, 29(6): 2635-2641. doi: 10.6038/pg20140625 [100] 卞爱飞, 於文辉, 周华伟. 频率域全波形反演方法研究进展[J]. 地球物理学进展, 2010, 25(3):982-993 doi: 10.3969/j.issn.1004-2903.2010.03.037 BIAN Aifei, YU Wenhui, HOU Huawei. Progress in the frequency-domain full waveform inversion method [J]. Progress in Geophysics, 2010, 25(3): 982-993. doi: 10.3969/j.issn.1004-2903.2010.03.037 [101] 杨午阳, 王西文, 雍学善, 等. 地震全波形反演方法研究综述[J]. 地球物理学进展, 2013, 28(2):766-776 doi: 10.6038/pg20130225 YANG Wuyang, WANG Xiwen, YONG Xueshan, et al. The review of seismic Full waveform inversion method [J]. Progress in Geophysics, 2013, 28(2): 766-776. doi: 10.6038/pg20130225 [102] Guasch L, Warner M R, Ravaut C. Adaptive waveform inversion: Practice [J]. Geophysics, 2019, 84(3): R447-R466. doi: 10.1190/geo2018-0377.1 [103] Chen G X, Wu R S, Chen S C. Reflection multi-scale envelope inversion [J]. Geophysical Prospecting, 2018, 66(7): 1258-1271. doi: 10.1111/1365-2478.12624 [104] Chen G X, Chen S C, Yang W C. Reflection waveform inversion based on full-band seismic data reconstruction for salt structure inversion [J]. Geophysical Journal International, 2020, 220(1): 235-247. doi: 10.1093/gji/ggz442 [105] Hu Y, Wu R S, Han L G, et al. Joint Multiscale direct envelope inversion of phase and amplitude in the time –frequency domain [J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 7(7): 5108-5120. [106] Wang G C, Alkhalifah T, Wang S X. Enhancing low-wavenumber information in reflection waveform inversion by the energy norm born scattering [J]. IEEE Geoscience and Remote Sensing Letters, 2020, 19: 8000205. [107] 胡勇, 黄兴国, 陈玉婷, 等. 基于反射地震数据的时频域包络反演[J]. 地球物理学进展, 2021, 36(5):1988-1994 doi: 10.6038/pg2021FF0195 HU Yong, HUANG Xingguo, CHEN Yuting, et al. Reflection seismic data based envelope inversion in the time-frequency domain [J]. Progress in Geophysics, 2021, 36(5): 1988-1994. doi: 10.6038/pg2021FF0195 [108] Ratcliffe A, Jupp R, Wombell R, et al. Full-waveform inversion of variable-depth streamer data: An application to shallow channel modeling in the North Sea [J]. The Leading Edge, 2013, 32(9): 1110-1115. doi: 10.1190/tle32091110.1 -
点击查看大图
图(8)
计量
- 文章访问数: 445
- HTML全文浏览量: 102
- PDF下载量: 24
- 被引次数: 0
