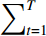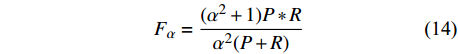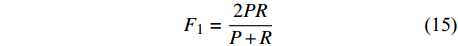Shipwreck identification with side scan sonar image based on fractal texture
-
摘要: 为提高侧扫声呐图像中沉船等目标信息的识别精度和识别效率，根据盒维数、毯维数与多重分形谱的侧扫声呐图像纹理特征提取算法，构建了基于分形纹理特征的Adaboost级联分类器沉船目标识别流程。结合实测侧扫声呐图像数据进行水下沉船识别实验，并与灰度共生矩阵和Tamura纹理特征的识别结果进行对比。研究表明，基于分形纹理特征的识别方法综合考虑了图像全局与局部纹理特征，且不依赖人工选取阈值参数与特征向量，可有效提高目标识别精度和识别效率。Abstract: In order to improve the accuracy and efficiency for recognition of underwater targets, fractal texture features including box dimension, blanket dimension and multifractal spectrum are calculated by texture feature extraction algorithm with side scan sonar images, and the shipwreck identification procedure based on Adaboost cascade classifier is constructed. The shipwreck recognition experiments have been carried out, and the results are compared. Research shows that the recognition method based on fractal texture features comprehensively considers the global and local texture features of the image, and does not rely on manual selection of threshold parameters and feature vectors, which can improve the accuracy and efficiency of target recognition.
-
水下目标识别技术被广泛应用于水下搜救、天然气水合物探测、石油勘探、沉船搜寻、水下考古等领域[1]。其中，水下沉船识别技术在航道疏浚和安全保障、水下考古和文物发掘等多应用领域有着重要的意义。侧扫声呐系统具有测量范围大、分辨率高等优点，可高效完成大面积海域的水下目标探测，广泛应用于水下沉船识别工作。受复杂海洋环境影响，侧扫声呐的目标影像往往存在图像模糊、畸变以及与其他成像体（如鱼群或悬浮物等）相似度高等问题[2]。因此，高精度的侧扫声呐图像分类提取算法是对沉船等目标进行有效识别的关键。
目前，侧扫声呐图像的目标识别算法通常基于图像分割法、支持向量机法、卷积神经网络法、纹理特征分类法等。其中，基于图像分割的方法主要根据声呐图像中遮蔽物体存在反射区与阴影区临近的现象识别沉船，但其聚类往往受到岩体、海脊和沙波的干扰而出现误识别[3]；支持向量机法使用沉船轮廓的不变矩进行沉船目标识别[4]，但由于其声呐图像多由测量实验池获得，缺失海底复杂地形与底质类型的特性，其运用于复杂海底环境存在一定局限性；卷积神经网络法基于像素重要性值，通过提取图像内点特征及其聚集度来识别目标，但由于声呐图像数据量较小，导致卷积神经网络在分类时易存在过拟合的现象，错将非目标物体识别为目标物体[5]。
受载体运动状态及海洋环境噪声影响，侧扫声呐图像多存在目标边界残缺及目标被部分遮挡的问题，目标的形状往往与实际有较大差异。对图像中的特定目标识别时，同一类目标的轮廓存在多样性且在不同的成像条件下其轮廓形状也存在差异。由于人工目标不具有自然景物的自相似性纹理，纹理特征分类法对轮廓多样的人工目标具有更好的识别效果。常用于侧扫声呐图像目标识别的纹理特征有灰度共生矩阵GLCM（Gray-level Co-occurrence Matrix）和Tamura纹理。灰度共生矩阵基于图像邻域像素灰度值的概率分布提取纹理特征[6-7]，能较好描述具有方向性和灰度差异大的纹理图像，但统计特征量的计算量庞大且特征量之间大多存在统计相关，寻找统计无关的特征量组合是一件繁杂的工作。基于人类对纹理视觉感知的心理学研究，Tamura在1978年提出图像的六个特征值来描述图像纹理[8]，其具有良好的旋转不变性与尺度不变性，但对于图像局部纹理特征难以描述。分形纹理基于图像像素灰度值的空间分布与自相似性描述提取图像纹理特征。Hausdorff提出分形维数用于定量描述图像表面的空间复杂程度，能够定量描述目标的纹理特征。Grassberger进一步使用多重分形谱用于描述不同测度子集下的局部图像纹理特征，能够结合整体纹理与局部纹理的相对关系描述目标特征。同时分形纹理特征提取避免了人工干预的低效，因而是一种良好的目标识别方法。
本文针对三种分形纹理特征提取，实现了盒计数分形算法、双毯覆盖模型分形算法与多重分形谱分形算法。针对侧扫声呐小样本目标识别易过拟合、分类精度低等问题，采用解释性好、抗干扰强的Adaboost级联分类器，构建基于分形纹理特征的Adaboost级联分类器沉船目标识别流程，并采用精确率和召回率的调和平均值F1作为沉船识别精度评价标准。结合实测数据进行沉船识别实验，分析比较了三种分形纹理特征的识别效果，并与灰度共生矩阵GLCM和Tamura纹理特征的识别结果进行对比，验证了本文方法的有效性。
1. 分形理论与分形纹理特征
近年来，分形理论在图像处理领域中取得了广泛的应用，包括边缘检测、目标识别、压缩编码等[9-12]，其中已在遥感图像、医学图像以及交通图像分类识别中取得一定成果[13-15]。分形是用于描述集合的空间复杂程度的一种度量，能够定量地描述图像表面的复杂性和不规则度。因此分形维数可以用于描述图像纹理特征。Grassberger提出了多重分形谱来描述不同测度子集下的局部图像纹理特征，能够从局部到整体全面地描述目标特征，这也为更准确的目标识别提供了理论依据[16]。
分形维数可用于描述二维图像表面纹理的复杂程度，Hausdorff定义了分形理论中关于测度和维数这二者的概念[17]。Hausdorff测度外延了在传统欧几里得几何学中所描述的长度、面积和体积的概念，其所能描述的对象既可以是欧氏几何图形，也可以是分形。定义H s（F）为F的s维Hausdorff测度，随着s的变化，存在使H s（F）从∞变化到0的临界值s0，其定义为Hausdorff维数，记作dH（F），即：
$$ {d}_{H}(F)=\mathrm{inf}\left\{s:{H}^{s}(F)=0\right\}=\mathrm{sup}\left\{s:{H}^{s}(F)=\infty \right\}$$ (1) Hausdorff维数对于任何集合都适用，因此具有很高的理论价值，但Hausdorff维数难于直接计算，本文采用下面的盒维数和毯维数进行简化计算。
1.1 盒维数
Gangepain和Roques-Carmes在1986年提出基于盒计数（Box-counting）的分形维数，通过计算覆盖图像表面的最小盒子数来度量[18]。将M×M的图像分为N×N的子块，图像（x, y）处的灰度值为f（x, y），总的灰度级为G。此时将图像看作三维物体的表面灰度集（x, y, f（x, y））。XY平面上是N×N的网格，Z轴为网格内像素灰度值，每个网格上有若干个盒子叠加，盒子高度h=[G×N/M]。
若在第（i, j）个网格中，第m个盒子中包含网格内灰度最小值，第l个盒子包含网格内灰度最大值，则覆盖第（i, j）个网格的盒子数nr（i, j）为：
$${n_r}(i,j) = l - m + 1$$ (2) 覆盖整个图像的盒子数Nr为：
$${N_r} = \sum\limits_{i,j} {{n_r}(i,j)} $$ (3) 其中r=M/N，由此可求分形维数D为：
$$D = \lim \frac{{\log ({N_r})}}{{\log (1/r)}}$$ (4) 通过改变网格N的大小计算一组Nr，然后计算点对{log（1/r）,log（Nr）}的线性回归，其斜率即是分形维数D。
1.2 毯维数
Mandelbrot在计算英国海岸线长度时提出了毯维数算法。近年来，国内也有应用毯维数进行海岸线长度计算的案例，取得了较好的效果[19-20]，其后衍生出可用于描述图像纹理的基于双毯覆盖模型的分形算法。图像的“毯子”由各像素灰度值作Z轴所形成的三维曲面上下ε处构建，其厚度为2ε，表面积为体积除以2ε。
令f（i, j）表示灰度函数，με表示“毯子”的上表面，bε表示“毯子”的下表面，初始情况设为：
$${u_0}(i,j) = {b_0}(i,j) = f(i,j)$$ (5) “毯子”生长算法如下：
$$\begin{split}{u_\varepsilon }(i,j) =& \max \{ {u_{\varepsilon - 1}}(i,j) + 1,\mathop {\max }\limits_{d(i,j,m,n) \leqslant 1} {u_{\varepsilon - 1}}(m,n)\} ,\\\varepsilon =& 1,2,3\cdots\end{split}$$ (7) $$\begin{split}{b_\varepsilon }(i,j) =& \min \{ {b_{\varepsilon - 1}}(i,j) + 1,\mathop {\min }\limits_{d(i,j,m,n) \leqslant 1} {b_{\varepsilon - 1}}(m,n)\} ,\\\varepsilon =& 1,2,3\cdots\end{split}$$ (7) 其中，d（i, j, m, n）为（i, j）与（m, n）两点间的距离。
则“毯子”的体积为：
$${v_\varepsilon } = \sum\limits_{i,j} {({u_\varepsilon }(i,j) - {b_\varepsilon }(i,j))} $$ (8) 表面积为：
$$A(\varepsilon ) = \frac{{{v_\varepsilon }}}{{2\varepsilon }}$$ (9) 由于分形表面积为A（ε）=Fε2−D，其中D为分形维数，令c1=2−D，则
$$\log A(\varepsilon ) = {c_1}\log \varepsilon + {c_0}$$ (10) 改变尺度ε的大小，可以计算得到一组log A（ε）的值，然后计算点对{ε, log A（ε）}线性回归，得到回归方程的斜率c1，即可求出分形维数D。
1.3 多重分形谱
多重分形常用来描述图像的奇异性几率分布，其能够量化测度的奇异结构，以及在尺度发生变化时以伴随有不同范围幂定律的现象建立模型，因此能够用于描述图像的纹理特征[21]。设α为Lipschitz-holder指数，又称奇异性指数，其决定了概率密度的奇异性。首先计算图像上每个点的奇异指数α，将具有相同奇异指数的像素点作为一个点集；然后计算具有不同奇异指数像素点集的分形维数，即可以得到多重分形谱图像α-f（α）[22]，计算过程如下：
（1）用尺度为δ的盒子覆盖图像，将像素点落在第i个盒子概率定为pi（δ），即得到概率测度分布为：
$${\mu _i}(q,\delta ) = \frac{{{{[{p_i}(\delta )]}^q}}}{{\displaystyle\sum\limits_i {{{[{p_i}(\delta )]}^q}} }}$$ (11) 其中，∑i[pi（δ）]q为所有盒子概率的q阶矩之和。
（2）对于概率测度分布的q阶矩，理论上q的取值范围为−∞＜q＜+∞。当q＞0时，在概率测度求和中具有较大概率的子集对分形维数的贡献较大；当q＜0时，具有较小概率的子集对分形维数的贡献较大。
此时，奇异指数α（q）为：
$$\alpha (q) = \mathop {\lim }\limits_{\delta \to 0} \frac{{\displaystyle\sum\limits_i {{\mu _i}(q,\delta )\ln \left[ {{p_i}(\delta )} \right]} }}{{\ln \delta }}$$ (12) 分形维数f（α（q））为：
$$f(\alpha (q)) = \mathop {\lim }\limits_{\delta \to 0} \frac{{\displaystyle\sum\limits_i {{\mu _i}(q,\delta )\ln \left[ {{\mu _i}(q,\delta )} \right]} }}{{\ln \delta }}$$ (13) （3）取一组不同的q值重复上述计算过程，绘制每个奇异指数α（q）对应的分形维数f（α（q））即得到了多重分形谱α−f（α）。其中α−f（α）曲线包括最小奇异指数αmin、最大奇异指数αmax、最小分形维数值fmin、最大分形维数值fmax、多重分形谱宽Δα=αmax−αmin和多重分形谱高Δf=fmax−fmin。
多重分形谱能够用来描述纹理图像的层次特征，即具有不同奇异指数的局部图像纹理。在区分自然场景中的人造物体时，人造物体本身不具有自相似性结构的特点，不满足分形模型，而自然景物存在自相似性，满足分形模型[23-24]。因此，沉船目标与海底表面的分形维数不同，便可以实现分形纹理对沉船识别的特征描述。多重分形方法通过奇异指数考虑了图像的局部与不同层次的纹理特征，因而能够全面且准确地描述图像分形结构，从而区分自然场景与人工造物，提高沉船目标识别的有效性。
2. 基于分形纹理特征的Adaboost目标识别
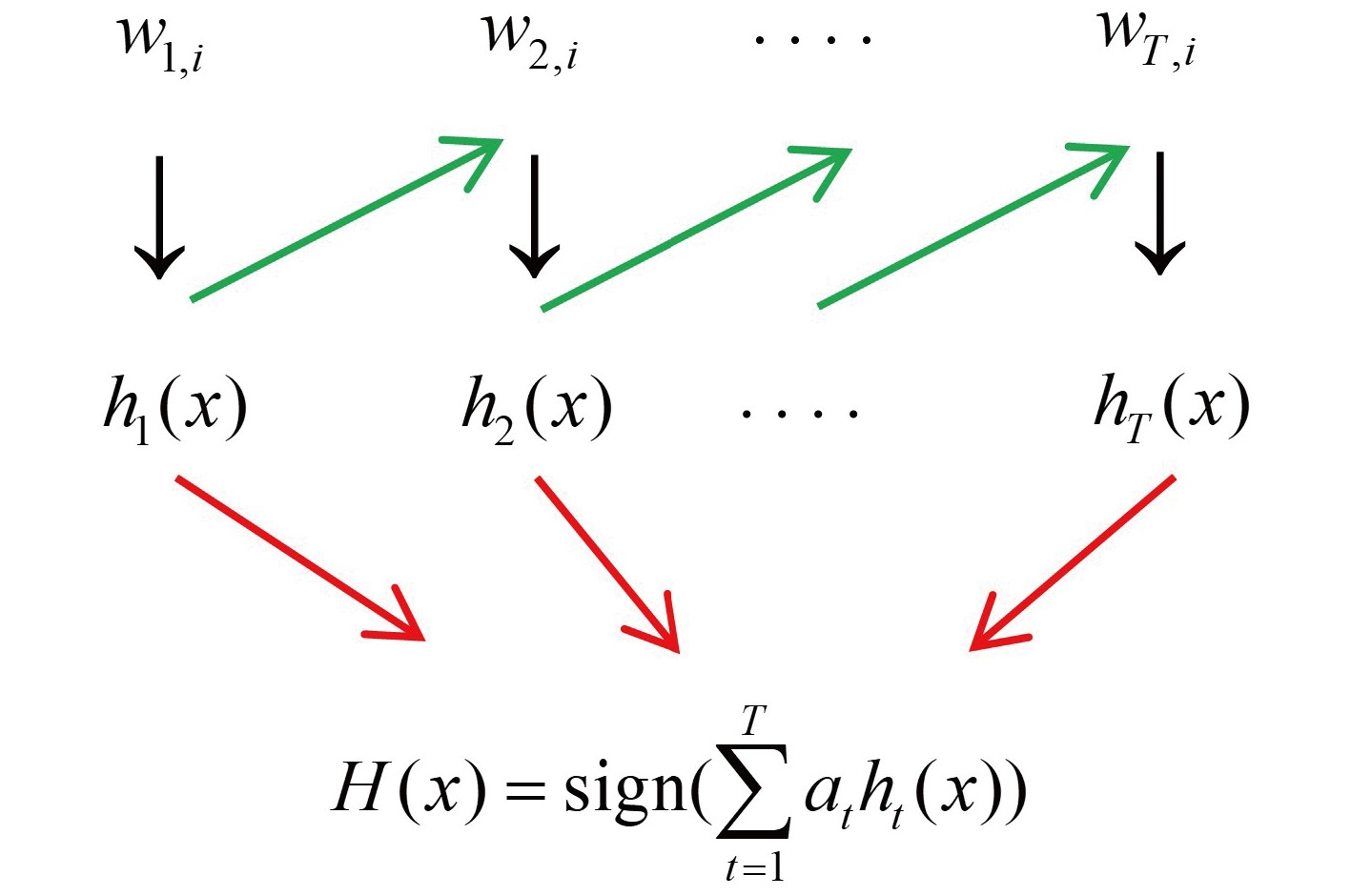
级联分类器Adaboost是一种基于boosting算法的改进算法，即是把“弱学习算法”提升为“强学习算法”，在人脸识别、交通标志检测、医学影像识别中均取得了良好的效果[25]。如图1所示，其通过选取多个弱分类器按照给定的样本集进行训练，每一个弱分类器的分类结果按照不同的权重对最终分类结果进行贡献。
2.1 Adaboost分类器介绍
本文采用简单决策树为弱分类器的Adaboost级联分类器作为侧扫声呐图像沉船识别分类器，主要计算过程如下：
（1）设训练样本集为S=（x1, y1）,（x2, y2）,···（xm, ym），若yi取值为−1或+1，则为二分类问题，其中1, ···, m为样本编号，ym为样本类别的标记。初始化样本权值w1, i=1/m，迭代次数为t=1, 2, ···, T。
（2）首先调用弱分类器学习算法，计算加权分类误差，再通过最小化加权分类误差ε选取一个最佳的分类器h（x, f, p, θ），其中p为不等号方向，f为特征向量，θ为阈值参数。
（3）令ht（x）=h（x, ft, pt, θt）, ft, pt, θt为使εt最小时的因子，则更新下一轮迭代权重为，wt+1,i=wt,i exp（−atytht（xi））/Zt，其中Zt为归一化因子。
（4）输出强分类器H(x) = sign(
$ {\displaystyle\sum }_{t=1}^{T} $ atht（x））, at=ln（（1−εt）/εt）。Adaboost算法的工作机制是从训练集初始权重训练出弱分类器1，根据其分类误差来更新训练样本的权重，使得误差较高的样本在弱分类器1中的权重变高，从而在接下来的弱分类器2中得到更多重视，如此重复进行直到指定的T个弱分类器训练完毕，通过集合策略进行整合得到最终的强分类器。因此，Adaboost分类器具有分类精度高、弱分类器可用多种回归分类模型构建、结构简单易理解、更能抵抗过拟合等优点。其他常用于二分类的分类器中，卷积神经网络容易发生过拟合、中间过程不可解释；K最近邻算法每一次分类均会重新全局运算，效率较低且需要人工K值选择；支持向量机对于小样本分类具有优势，但核函数可解释性较差。因此本文采用简单决策树为弱分类器的Adaboost级联分类器作为侧扫声呐图像沉船识别分类器。
在机器学习和目标分类等领域中，如何评估分类结果的精度是一个重要的工作，本文引入F-measure评价模型[26]。F-score是精确率P和召回率R的加权调和平均，当参数α增大时，召回率的权重增加，精确率的权重降低；当参数α减小时，召回率的权重降低，精确率的权重增加。
$${F_\alpha } = \frac{{({\alpha ^2} + 1){{P}}*{{R}}}}{{{\alpha ^2}({{P}} + {{R}})}}$$ (14) 当参数α=1时，即认为精确率和召回率的权重是一样的。此时F1值就是精确率和召回率的调和平均值，能够较为准确地评价分类器分类结果，即：
$${F_1} = \frac{{2PR}}{{P + R}} $$ (15) 2.2 Adaboost目标识别流程
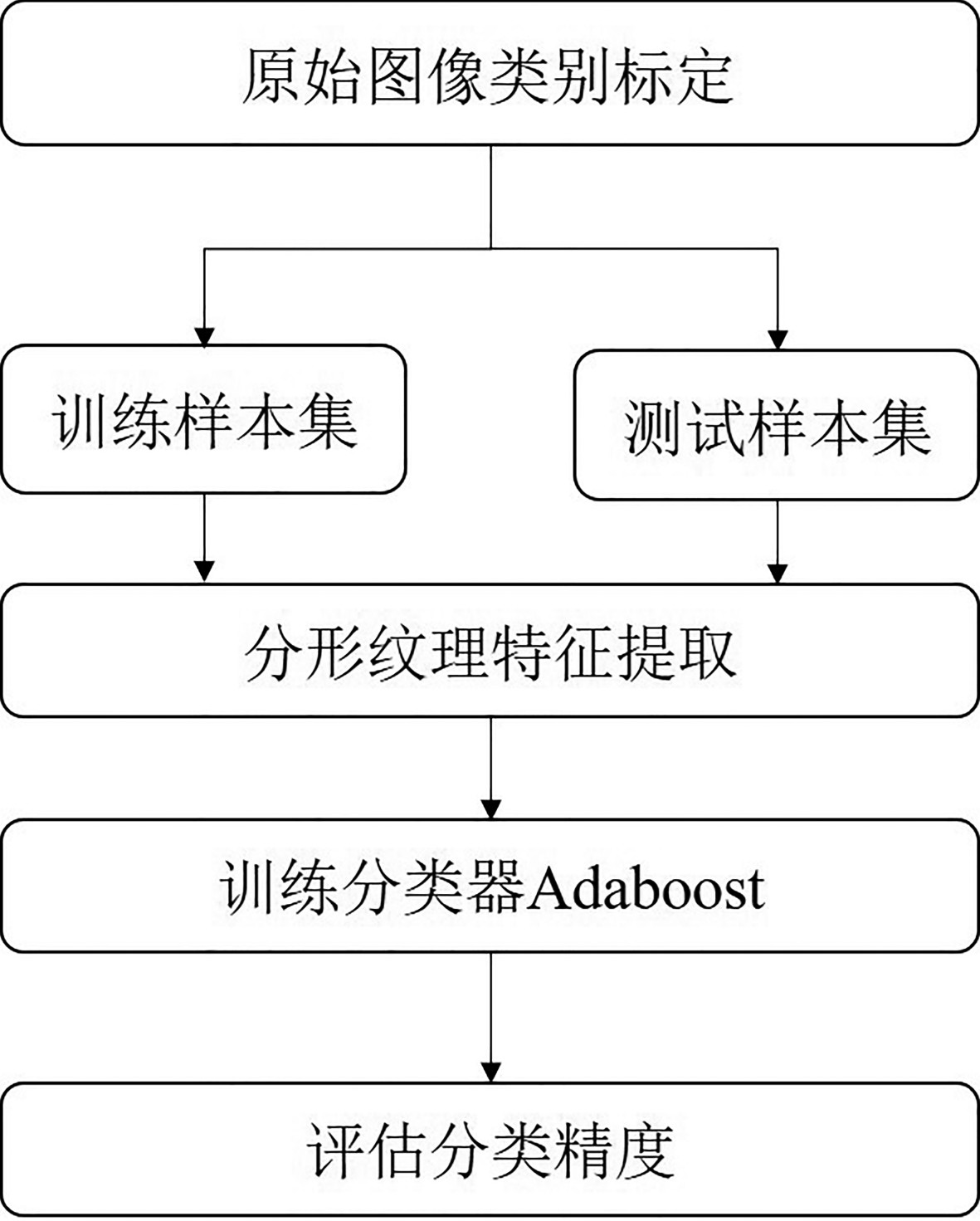
本文构建了基于分形纹理特征的Adaboost目标识别流程，如图2所示。
![]()
图 2 基于分形纹理特征的Adaboost目标识别流程Figure 2. Adaboost target recognition procedure based on fractal texture features第1步，将样本分为训练样本和测试样本两部分（均已人工标定其类别标签），训练样本与测试样本中均包含若干沉船图像和非沉船图像。
第2步，根据盒维数、毯维数与多重分形谱计算流程，计算训练和测试样本的分形纹理特征向量。
第3步，将训练样本的分形纹理特征向量输入级联分类器Adaboost中进行训练，然后输入测试样本的分形纹理特征向量，预测每一个测试样本的类别。
第4步，根据分类器分类结果计算F1值。
针对侧扫声呐小样本目标识别易过拟合、分类精度低的问题，常用分类器在使用中存在一定问题难以解决，如支持向量机解释性较差，卷积神经网络容易过拟合，K最近邻算法计算效率低且参数需人工干预。因此本文采用解释性好、抗干扰强的Adaboost级联分类器，构建基于分形纹理特征的Adaboost分类器沉船目标识别流程，并使用精确率和召回率的调和平均值F1作为沉船识别精度评价标准。
3. 实验与讨论
3.1 基于分形纹理特征的Adaboost识别实验
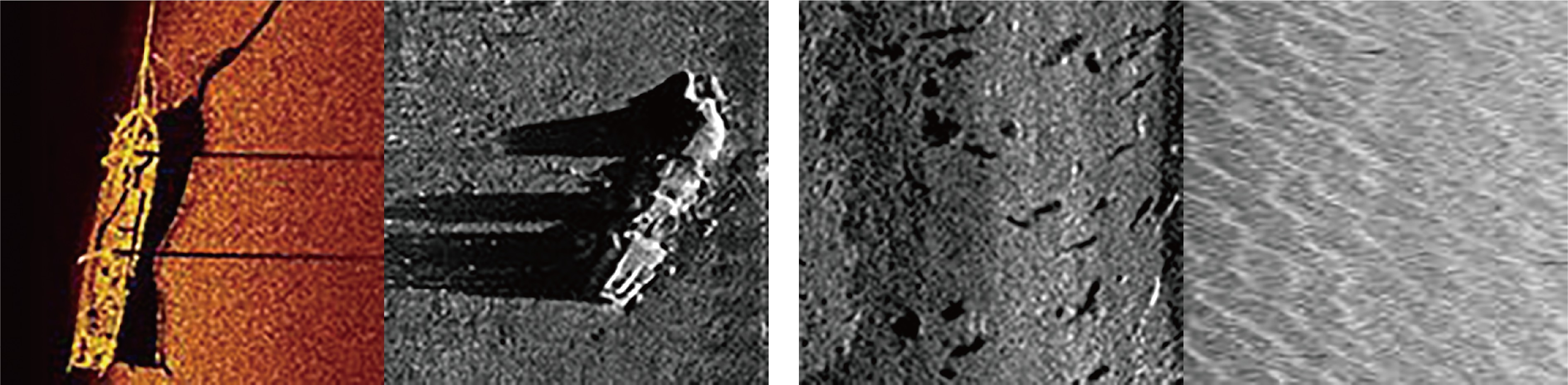
本文通过选取各个侧扫声呐仪器厂商网站以及沉船搜寻网站上展列的侧扫声呐图片为包含沉船目标的正样本，共47张，通过截取普利茅斯湾侧扫数据不包含沉船目标的负样本（鱼和海底表面）共105张图片，图片大小为128×128。随机选取正样本28张、负样本71张作为训练数据来训练分类器，余下的正样本19张、负样本34张作为测试数据来测试分类器的训练效果（图3）。
![]()
图 3 目标识别中的正样本与负样本左为正样本示例[27]，右为负样本示例。Figure 3. Positive and negative samples in target recognitionLeft is positive sample, right is negative sample.（1）盒维数分类结果
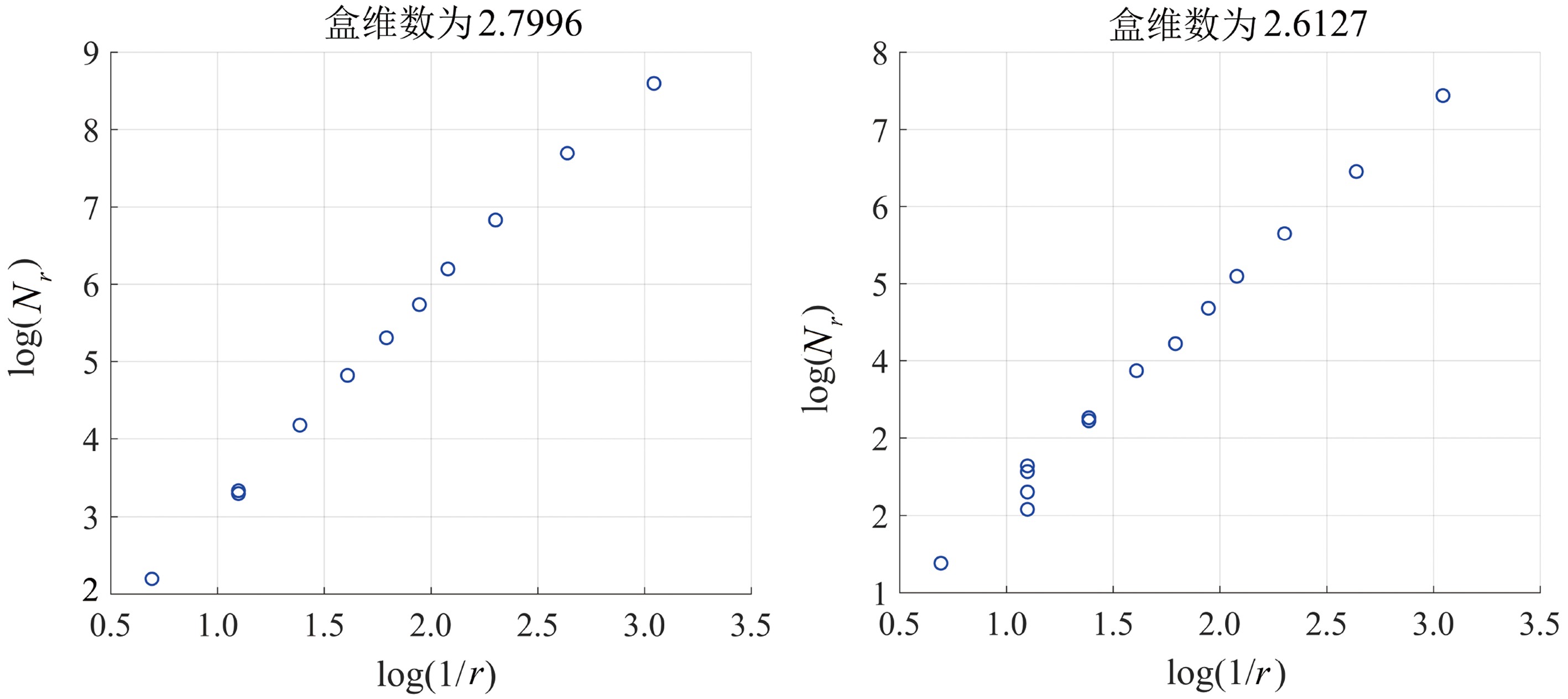
根据1.1节提出的盒维数计算方法计算得到每张图像对应的盒维数值。图4展示了部分沉船目标和非目标的盒维数。
![]()
图 4 盒维数计算左为正样本结果，右为负样本结果。Figure 4. Box dimension calculationLeft is positive sample result, right is negative sample result.（2）毯维数分类结果
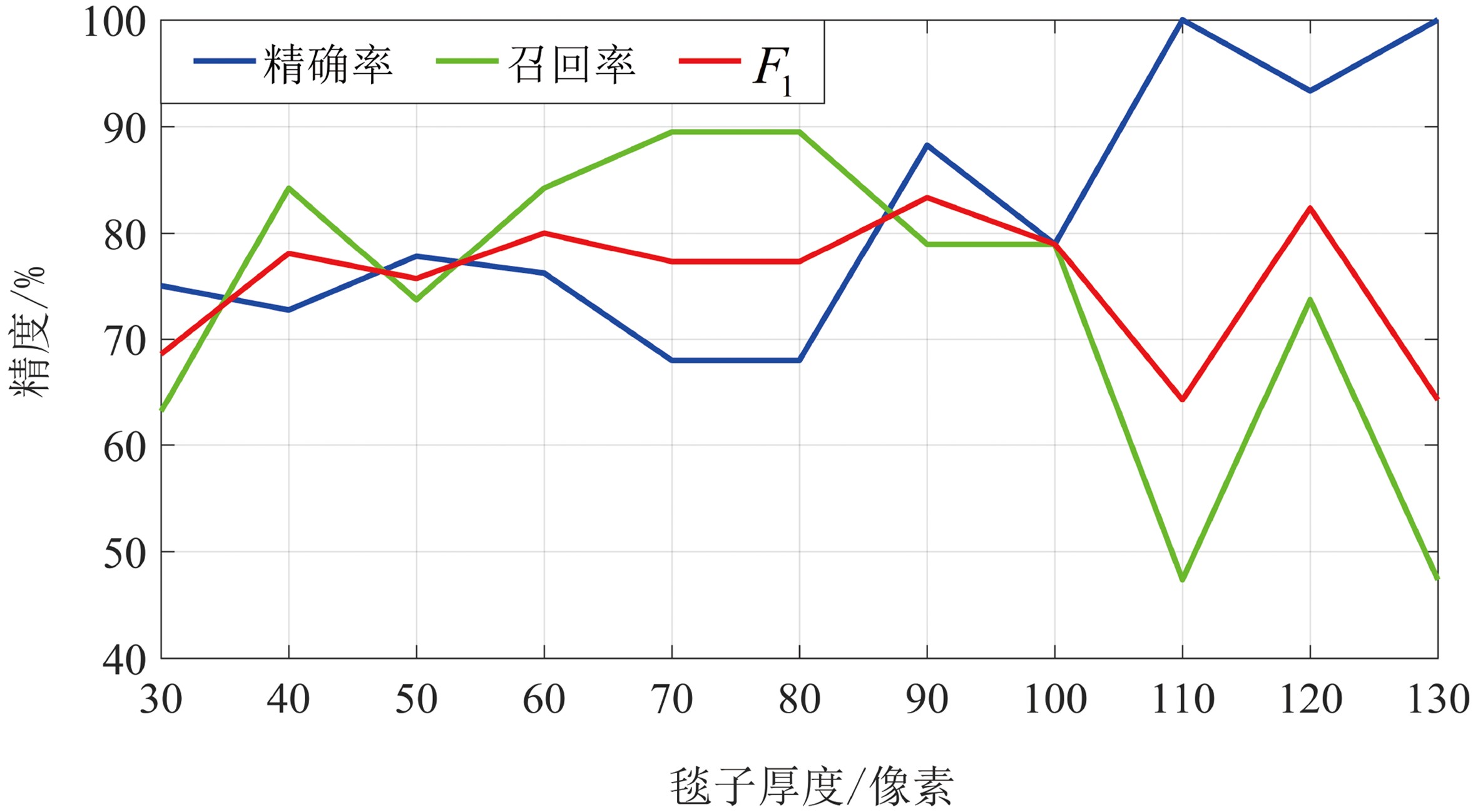
对于给定的毯子厚度ε可以求出其毯维数值，在此通过对比不同毯子厚度ε对分类结果的影响来寻找最佳毯子厚度，如图5所示。
![]()
图 5 不同毯子厚度的分类结果比较Figure 5. Comparison of classification results of different blanket thicknesses由图5可知，随着毯子厚度的增大，沉船识别的精确率大体逐渐上升，而沉船的召回率逐渐下降，表明当毯子厚度大于100时，召回率较低，表示毯维数对沉船图像纹理特征描述过拟合，从而降低了对不同情况下沉船目标的描述程度，即识别沉船的能力不足。此时F1值在毯子厚度为90时取得最大值83.3%。因此本文选择毯子厚度为90时的毯维数作为其最优纹理特征。
（3）多重分形谱分类结果
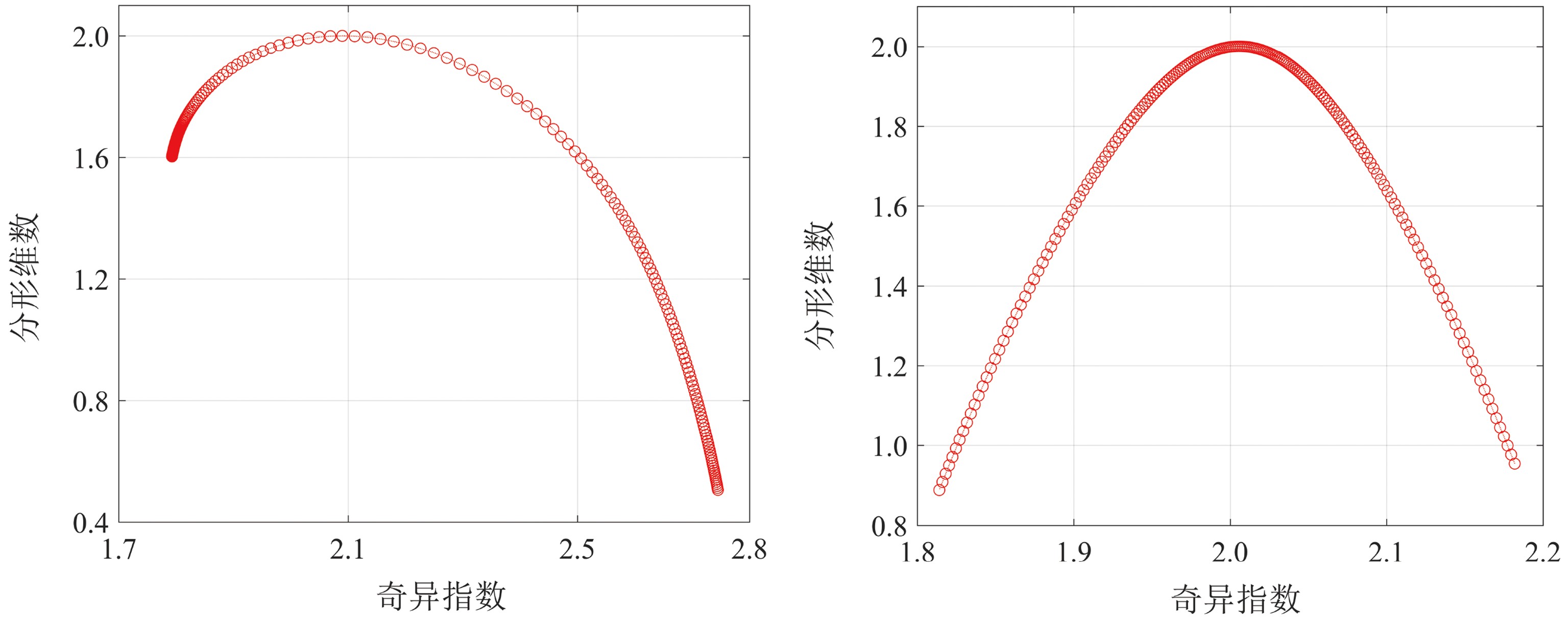
根据1.3节提出的多重分形谱计算公式，本文绘制了沉船正样本和其他非沉船负样本的α-f（α）多重分形谱，如图6所示。部分沉船及非沉船目标多重分形谱参数见表1。
![]()
图 6 不同样本的多重分形谱结果左为正样本，右为负样本。Figure 6. Multifractal spectrum of different samplesLeft is positive samples, right is negative samples. Horizontal axis α is singularity index, and vertical axis f（α）is fractal dimension.表 1 沉船及非沉船目标的多重分形谱参数Table 1. Parameters of multifractal spectrum of shipwrecked and non-wrecked targets目标 αmin αmax fmin fmax Δα Δf 沉船1 1.81 2.96 0.07 2.00 1.15 1.93 沉船2 1.92 2.21 1.68 2.00 0.29 0.32 沉船3 1.90 2.35 1.13 2.00 0.45 0.87 非沉船1 1.99 2.04 1.75 2.00 0.05 0.25 非沉船2 1.98 2.05 1.75 2.00 0.07 0.25 非沉船3 1.96 2.03 1.80 2.00 0.07 0.20 注：①αmin和αmax分别代表了图像测度集的最小概率和最大概率，其差值Δα表明图像在概率测度分布中的差异程度，Δα越大则图像各测度区域和分形层次的区别越大，多重分形性质越明显；Δα越小则图像各测度区域和分形层次的区别越小，多重分形性质越微弱。
②fmin和fmax分布代表了图像测度集的最大值和最小值，其差值Δf表明图像在图像测度子集纹理复杂程度上的差异，Δf差值越大则表明图像不同测度子集纹理区别越明显。3.2 三种分形纹理特征识别结果与讨论
比较了盒维数、毯维数、多重分形谱三种分形纹理特征提取方法对侧扫声呐图像沉船目标的识别效果，如表2所示。
表 2 分形纹理特征识别结果Table 2. Recognition of fractal texture feature识别方法 精确度/% 召回率/% F1/% 盒维数 50 78.95 61.2 毯维数 88.2 78.9 83.3 多重分形谱 95 100 97.4 在三种分形纹理特征中，多重分形谱特征的精确度和召回率均远高于盒维数与毯维数两种分形纹理特征，其F1值为97.4，高于盒维数的61.2与毯维数的83.3，因而多重分形谱的侧扫声呐图像沉船目标识别效果最好，这表明多重分形谱纹理特征对沉船目标的描述全面性和分辨沉船目标与非目标区的区分能力较其他两种方法要好。
单一分形维数（盒维数和毯维数）盒维数纹理特征识别效果最差，其原因是其仅仅反映的是单一尺度下整张图像的纹理复杂程度，无法描述图像局部纹理信息，对于一些整体纹理较为复杂的非沉船目标，如含有鱼群的声呐图像，往往会误判为沉船图像，因此其从非沉船目标中对沉船目标的区分性不足，识别的精确率较低。
多重分形谱纹理特征的优点在于对不同的图像概率测度子集分别计算其分形维数，有效地描述了图像局部纹理特征，即使存在某些鱼群或海底地表的纹理在整体上和沉船目标上较为相似，其局部纹理特征也往往存在明显的差异，且不同种类的目标其多重分形谱的性质区别很大，因而多重分形谱获得了很好的沉船识别效果。
3.3 其他纹理特征识别结果与讨论
为了验证分形纹理特征在侧扫声呐图像沉船目标识别中的效果，本文拟采用两种常用的纹理特征提取方法作为对比实验，即灰度共生矩阵GLCM与Tamura纹理特征。GLCM选择最常用的6个特征值即角二阶距、逆差距、熵、对比度、非相似性、相关性。计算特定距离d下的4个方向的灰度共生矩阵，用6种特征值的均值与方差作为其特征向量，以抵消沉船的方向性对于目标识别的干扰。Tamura选择六特征值作为图片的特征向量，即粗糙度、对比度、方向度、线性度、规整度和粗略度。实验数据与分类器选取均与3.1节相同，沉船目标识别结果见表3所示。
表 3 多重分形谱、GLCM、Tamura三种纹理特征识别结果Table 3. Recognition results of multifractal spectrum, GLCM and Tamura识别方法 精确率/% 召回率/% F1/% 多重分形谱 95 100 97.4 GLCM（d=10） 100 94.7 97.2 Tamura六特征值 94.1 84.2 88.9 从图像尺度的角度考虑，Tamura纹理特征所提取的六特征值仅有规整度一个值能够描述图像的局部特征，其他5个特征值均是对整张图像的尺度进行灰度统计的结果，因而很难全面描述沉船图像的纹理特征；而GLCM对距离参数d的取值不同可以理解为统计不同尺度下的图像局部特征（像素点对灰度值出现频率）来描述沉船图像的纹理特征，因此，当寻找到最佳距离参数d时则表明在该尺度下获取的纹理特征对沉船描述最好，因而识别效果较好；在多重分形谱方法中，通过不同奇异指数将图像划分为不同测度子集，统计每一个子集的纹理特征形成多重分形谱。从多尺度的角度将沉船图像整体到局部的纹理特征结合起来描述沉船目标，取得了最优的识别结果。
4. 结论
（1）在三种分形纹理特征中，多重分形谱特征的识别精度F1远高于单一分形维数（盒维数与毯维数）。单一分形维数识别效果差，其原因是其仅仅反映单尺度下整张图像的纹理复杂程度，无法描述多尺度局部纹理信息。多重分形谱纹理特征对图像中不同的概率测度子集分别计算其分形维数，有效地描述了图像局部纹理特征。某些负样本整体纹理和沉船目标较为相似，但其局部纹理特征也往往存在明显的差异，在不同种类目标的多重分形谱上的谱型区别很大。多重分形谱能够从多尺度角度将正负样本进行区分，因此获得了最优的沉船识别效果。
（2）Tamura纹理特征六特征值中仅有规整度描述图像的局部特征，其他5个特征值均是对整张图像的尺度进行灰度统计的结果，因此识别精度F1优于单一分形维数，但弱于灰度共生矩阵和多重分形谱特征。灰度共生矩阵通过调整距离和方向参数来寻找识别效果最好的图像局部纹理特征，但此方法对每张图像都要重新寻找最佳参数，时间成本更高。因此相对常用的纹理特征，多重分形谱特征具有能够描述多尺度局部纹理，避免人工干预，识别效率高等优点，在沉船识别中也获得了最优的识别精度和识别效率。
-
![]()
图 2 基于分形纹理特征的Adaboost目标识别流程
Figure 2. Adaboost target recognition procedure based on fractal texture features
![]()
图 3 目标识别中的正样本与负样本
左为正样本示例[27]，右为负样本示例。
Figure 3. Positive and negative samples in target recognition
Left is positive sample, right is negative sample.
![]()
图 4 盒维数计算
左为正样本结果，右为负样本结果。
Figure 4. Box dimension calculation
Left is positive sample result, right is negative sample result.
![]()
图 5 不同毯子厚度的分类结果比较
Figure 5. Comparison of classification results of different blanket thicknesses
![]()
图 6 不同样本的多重分形谱结果
左为正样本，右为负样本。
Figure 6. Multifractal spectrum of different samples
Left is positive samples, right is negative samples. Horizontal axis α is singularity index, and vertical axis f（α）is fractal dimension.
表 1 沉船及非沉船目标的多重分形谱参数
Table 1 Parameters of multifractal spectrum of shipwrecked and non-wrecked targets
目标 αmin αmax fmin fmax Δα Δf 沉船1 1.81 2.96 0.07 2.00 1.15 1.93 沉船2 1.92 2.21 1.68 2.00 0.29 0.32 沉船3 1.90 2.35 1.13 2.00 0.45 0.87 非沉船1 1.99 2.04 1.75 2.00 0.05 0.25 非沉船2 1.98 2.05 1.75 2.00 0.07 0.25 非沉船3 1.96 2.03 1.80 2.00 0.07 0.20 注：①αmin和αmax分别代表了图像测度集的最小概率和最大概率，其差值Δα表明图像在概率测度分布中的差异程度，Δα越大则图像各测度区域和分形层次的区别越大，多重分形性质越明显；Δα越小则图像各测度区域和分形层次的区别越小，多重分形性质越微弱。
②fmin和fmax分布代表了图像测度集的最大值和最小值，其差值Δf表明图像在图像测度子集纹理复杂程度上的差异，Δf差值越大则表明图像不同测度子集纹理区别越明显。
下载: 导出CSV
表 2 分形纹理特征识别结果
Table 2 Recognition of fractal texture feature
识别方法 精确度/% 召回率/% F1/% 盒维数 50 78.95 61.2 毯维数 88.2 78.9 83.3 多重分形谱 95 100 97.4
下载: 导出CSV
表 3 多重分形谱、GLCM、Tamura三种纹理特征识别结果
Table 3 Recognition results of multifractal spectrum, GLCM and Tamura
识别方法 精确率/% 召回率/% F1/% 多重分形谱 95 100 97.4 GLCM（d=10） 100 94.7 97.2 Tamura六特征值 94.1 84.2 88.9
下载: 导出CSV
-
[1] 赵建虎, 王爱学. 精密海洋测量与数据处理技术及其应用进展[J]. 海洋测绘, 2015, 35(6):1-7 doi: 10.3969/j.issn.1671-3044.2015.06.001 ZHAO Jianhu, WANG Aixue. Precise marine surveying and data processing technology and their progress of application [J]. Hydrographic Surveying and Charting, 2015, 35(6): 1-7. doi: 10.3969/j.issn.1671-3044.2015.06.001
[2] 赵建虎, 王爱学, 王晓, 等. 侧扫声纳条带图像分段拼接方法研究[J]. 武汉大学学报: 信息科学版, 2013, 38(9):1034-1038 ZHAO Jianhu, WANG Aixue, WANG Xiao, et al. A segmented mosaic method for side scan sonar strip images using corresponding features [J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1034-1038.
[3] Rutledge J, Yuan W T, Wu J, et al. Intelligent shipwreck search using autonomous underwater vehicles[C]//2018 IEEE International Conference on Robotics and Automation (ICRA). Brisbane, QLD, Australia: IEEE, 2018: 6175-6182.
[4] 许文海, 续元君, 董丽丽, 等. 基于水平集和支持向量机的图像声呐目标识别[J]. 仪器仪表学报, 2012, 33(1):49-55 doi: 10.3969/j.issn.0254-3087.2012.01.008 XU Wenhai, XU Yuanjun, DONG Lili, et al. Level-set and SVM based target recognition of image sonar [J]. Chinese Journal of Scientific Instrument, 2012, 33(1): 49-55. doi: 10.3969/j.issn.0254-3087.2012.01.008
[5] 卞红雨, 陈奕名, 张志刚, 等. 像素重要性测量特征下的侧扫声呐目标检测[J]. 声学学报, 2019, 44(3):353-359 BIAN Hongyu, CHEN Yiming, ZHANG Zhigang, et al. Target detection algorithm in side-scan sonar image based on pixel importance measurement [J]. Acta Acustica, 2019, 44(3): 353-359.
[6] 郭军, 马金凤, 王爱学. 基于SVM算法和GLCM的侧扫声纳影像分类研究[J]. 测绘与空间地理信息, 2015, 38(3):60-63 doi: 10.3969/j.issn.1672-5867.2015.03.020 GUO Jun, MA Jinfeng, WANG Aixue. Study of side scan sonar image classification based on SVM and gray level co-occurrence matrix [J]. Geomatics & Spatial Information Technology, 2015, 38(3): 60-63. doi: 10.3969/j.issn.1672-5867.2015.03.020
[7] 高程程, 惠晓威. 基于灰度共生矩阵的纹理特征提取[J]. 计算机系统应用, 2010, 19(6):195-198 doi: 10.3969/j.issn.1003-3254.2010.06.047 GAO Chengcheng, HUI Xiaowei. GLCM-based texture feature extraction [J]. Computer Systems & Applications, 2010, 19(6): 195-198. doi: 10.3969/j.issn.1003-3254.2010.06.047
[8] 景军锋, 张缓缓, 李鹏飞, 等. LBP和Tamura纹理特征方法融合的织物疵点分类算法[J]. 计算机工程与应用, 2012, 48(23):155-160 doi: 10.3778/j.issn.1002-8331.2012.23.035 JING Junfeng, ZHANG Huanhuan, LI Pengfei, et al. Fabric defect classification based on local binary patterns and Tamura texture feature method [J]. Computer Engineering and Applications, 2012, 48(23): 155-160. doi: 10.3778/j.issn.1002-8331.2012.23.035
[9] 王瑞. 多重分形及其在图像识别中的应用研究[D]. 西北大学硕士学位论文, 2010. WANG Rui. Multifractal and its application in image recognition[D]. Master Dissertation of Northwest University, 2010.
[10] 徐文海. 基于分形理论的遥感影像纹理分析与分类研究[D]. 中南大学硕士学位论文, 2010. XU Wenhai. Texture analysis and classification of remote sensing image based on fractal theory[D]. Master Dissertation of Central South University, 2010.
[11] Femmam S. Texture classification approach based on 2D multifractal analysis[Z]. SPIE Newsroom, 2015.
[12] Lopes R, Betrouni N. Fractal and multifractal analysis: a review [J]. Medical Image Analysis, 2009, 13(4): 634-649. doi: 10.1016/j.media.2009.05.003
[13] Don S, Chung D, Revathy K, et al. A neural network approach to mammogram image classification using fractal features[C]//2009 IEEE International Conference on Intelligent Computing and Intelligent Systems. Shanghai, China: IEEE, 2009: 444-447.
[14] Cao W L, Shi Z K, Feng J H. Traffic image classification method based on fractal dimension[C]//2006 5th IEEE International Conference on Cognitive Informatics. Beijing, China: IEEE, 2006: 903-907.
[15] 李攀峰, 赵铁虎, 张晓波, 等. 山东半岛遥感解译断裂分形研究[J]. 海洋地质与第四纪地质, 2015, 35(4):105-112 LI Panfeng, ZHAO Tiehu, ZHANG Xiaobo, et al. Fractal research of remote sensing linear faults in Shandong peninsula [J]. Marine Geology & Quaternary Geology, 2015, 35(4): 105-112.
[16] Grassberger P. Generalized dimensions of strange attractors [J]. Physics Letters A, 1983, 97(6): 227-230. doi: 10.1016/0375-9601(83)90753-3
[17] Falconer K J. Fractal Geometry - Mathematical Foundations and Applications[M]. Chichester: Wiley, 1990.
[18] Gagnepain J J, Roques-Carmes C. Fractal approach to two-dimensional and three-dimensional surface roughness [J]. Wear, 1986, 109(1-4): 119-126. doi: 10.1016/0043-1648(86)90257-7
[19] Kisan S, Mishra S, Bhattacharjee G, et al. Analytical Study on Fractal Dimension-A Review[C]//2018 International Conference on Recent Innovations in Electrical, Electronics & Communication Engineering (ICRIEECE). IEEE, 2018: 380-384.
[20] 周江, 印萍, 程荡敌, 等. 基于GIS和分形理论研究的海岸线图像和分维以及长度[J]. 海洋地质与第四纪地质, 2008, 28(4):65-71 ZHOU Jiang, YIN Ping, CHENG Dangdi, et al. Research on the fractal simulation image and the fractal dimension and length of coastline based on GIS and fractal theory [J]. Marine Geology & Quaternary Geology, 2008, 28(4): 65-71.
[21] 李会方. 多重分形理论及其在图象处理中应用的研究[D]. 西北工业大学博士学位论文, 2004. LI Huifang. The study on multifractal theory and application in image processing[D]. Doctor Dissertation of Northwestern Polytechnical University, 2004.
[22] Turiel A, Del Pozo A. Reconstructing images from their most singular fractal manifold [J]. IEEE Transactions on Image Processing, 2002, 11(4): 345-350. doi: 10.1109/TIP.2002.999668
[23] Turiel A, Parga N. The multifractal structure of contrast changes in natural images: from sharp edges to textures [J]. Neural Computation, 2000, 12(4): 763-793. doi: 10.1162/089976600300015583
[24] Potlapalli H, Luo R C. Fractal-based classification of natural textures [J]. IEEE Transactions on Industrial Electronics, 1998, 45(1): 142-150. doi: 10.1109/41.661315
[25] Mahmood Z, Ali T, Khattak S. Automatic player detection and recognition in images using AdaBoost[C]//Proceedings of 2012 9th International Bhurban Conference on Applied Sciences and Technology (IBCAST). Islamabad, Pakistan: IEEE, 2012: 64-69.
[26] 李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 18-20. LI Hang. Statistical Learning Methods[M]. Beijing: Tsinghua University Press, 2012: 18-20.
[27] Scoville D. Steamer Homer Warren[Z/OL]. https://www.shipwreckworld.com/articles/side-scan-sonar-images/.
-
期刊类型引用(2)
1. 胡德胜，满晓，高铭恒，李文龙，余敏. 北部湾盆地乌石凹陷西洼烃源岩特征与勘探前景. 中国海上油气. 2025(01): 13-25 . 
百度学术
2. 杨勇，张世明，吕琦，孙志刚，蒋龙，孙红霞，刘祖鹏，吕晶，邢祥东，倪良田. 中国东部陆相断陷盆地页岩油开发理论认识与技术实践——以济阳页岩油为例. 油气地质与采收率. 2024(05): 1-15 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 2326
- HTML全文浏览量: 539
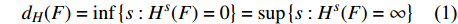
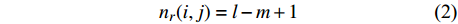
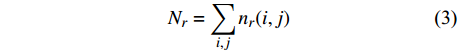
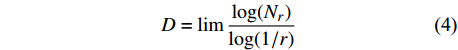
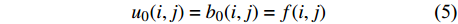
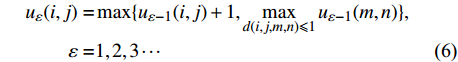
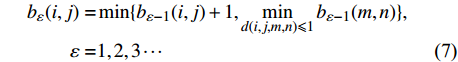
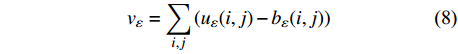
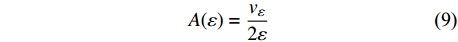
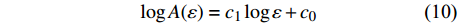
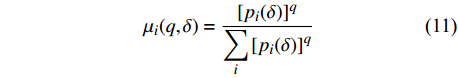
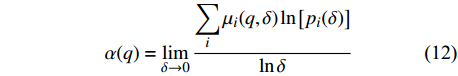
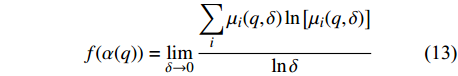
- PDF下载量: 61
- 被引次数: 2
