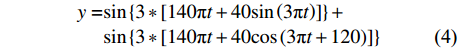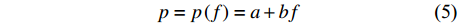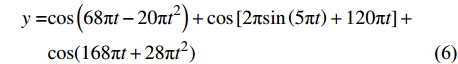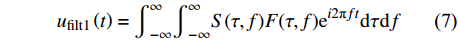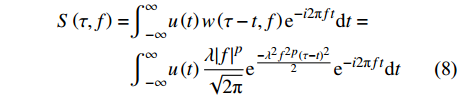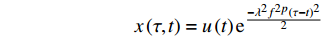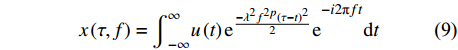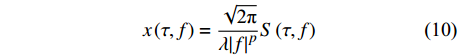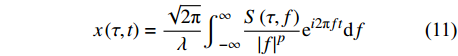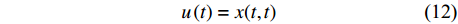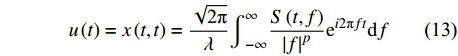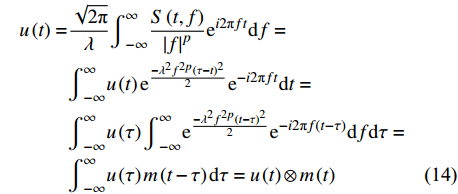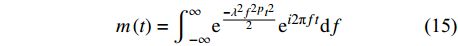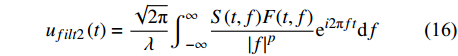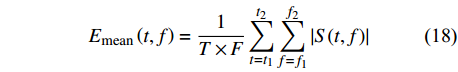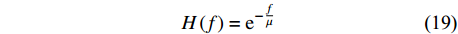Random noise suppression of marine seismic data based on improved generalized S transform
-
摘要: 常规广义S变换采用固定的高斯窗参数，在时频分析时不能够兼顾高低频端的信号，同时标准S逆变换在时频域滤波时会产生滤波噪音。本文提出了基于变频率高斯窗的广义S变换，同时改进了S逆变换公式。该方法不仅提升了信号时频谱的聚焦度，而且还消除了滤波噪音。通过计算包含随机噪声干扰信号的瞬时信噪比阈值，然后根据不同阈值有针对性的选择压制随机噪音的处理策略。合成数据和实际地震数据处理结果表明，该方法能够有效的压制随机噪音，提高地震数据信噪比。Abstract: Conventional generalized S transform (GST) uses fixed parameters for Gaussian window, which makes it impossible to take into account the high and low frequency signals in the time-frequency analysis. At the same time, the standard S inverse transform produces filtering noise when filtering in the time-frequency domain. In this paper, a generalized S transform based on variable frequency Gaussian window is proposed, and the inverse S transform formula is revised. This method not only improves the focus of the frequency spectrum of the signal, but also eliminates the filtering noise. By calculating the instantaneous signal-to-noise ratio threshold value of the signal containing random interference noise, and according to different threshold values, the processing strategy of suppressing the random noise is selected in a targeted manner. The processing results of synthetic data and actual seismic data show that the method can effectively suppress random noise and improve the signal-to-noise ratio of seismic data.
-
1. 研究背景
S变换[1]是由美国的地球物理学家Stockwell等[2-3]在短时傅里叶变换和小波变换的基础上提出的。与短时傅里叶变换和小波变换相比，S变换既解决了短时傅里叶变换时窗固定的问题，同时具有小波变换的多分辨率分析。由于S变换所具有的独特优势，其在信号分析和处理领域受到广泛关注。由于高斯时窗和频率的函数关系较为单一，降低了S变换在实际应用中的灵活性，因此很多学者从不同角度对S变换进行了推广和改进得到广义S变换[4-8]，使得广义S变换更加适用于地震资料处理、油气检测[9-11]等方面的信号处理。
广义S变换作为时频域的滤波工具，能够压制噪音从而提高地震资料信噪比[12]。赵淑红等[13]首先在频域和时域确定干扰波范围，再利用广义S变换处理VSP数据；李雪英等[14]考虑到地震信号有效频带随时间逐渐变窄，在时频域采用交互式的方法确定高频噪音切除边界；王云专等采用时频谱叠加的方法计算共中心点道集中的滤波器进而压制随机干扰[15]。陈学华等引入λ和p两个参数控制高斯窗函数的变化趋势，在应用过程中通过试验确定最优参数[5]。本文对陈学华[5]的广义S变换方法进行了改进，使其兼顾对高低频端信号的分析能力，能够更加适用于随机噪音压制；其次由于标准S逆变换存在能量泄露，通过修正S逆变换[16-19]，以消除滤波噪音。在压制噪音时，首先计算信号瞬时信噪比，根据瞬时信噪比的高低结合不同处理策略实现噪音压制。通过处理合成数据和实际资料，验证改进广义S正反变换在随机噪音压制方面的有效性。
2. 方法原理
2.1 改进广义S变换
信号u(t)的标准S正变换的表达式为
$$ \int S\left(\tau ,f\right)={\int }_{-\infty }^{\infty }u\left(t\right)w(\tau -t,f){\mathrm{e}}^{-i2{{\text π} }ft}\mathrm{d}t $$ (1) 式中，
$ S\left(\tau ,f\right) $ 是信号$ u\left(t\right) $ 的时频谱，$ w(t,f) $ 是高斯窗函数，其具体表达式为$$ w\left(t,f\right)=\frac{1}{\sigma \sqrt{2\mathrm{{\text π} }}}{\mathrm{e}}^{\frac{-{t}^{2}}{2{\sigma }^{2}}} $$ (2) 式中，
$ \sigma =\dfrac{1}{\left|f\right|} $ 是控制高斯窗宽度的尺度因子。广义S变换就是通过调节尺度因子大小控制对应的高斯窗函数的有效宽度。针对标准S变换高斯窗形态随频率变化趋势单一进而导致S变换时频谱聚焦度低的问题，陈学华等[5]在标准S变换的基础上引入了控制参数λ和p，目的为丰富尺度因子随频率的变化趋势，针对不同的资料提供更多的参数组合。其改进的尺度因子为
$$ \sigma =\frac{1}{\lambda {\left|f\right|}^{p}} $$ (3) 不同的控制参数λ和p影响尺度因子变化的快慢（图1）。不同的λ值对尺度因子的主要影响集中在低频端，即随着λ值的增大，同一频率对应的尺度因子幅值增大。不同的p值对尺度因子的主要影响在高频端，即随着p值的增大，同一频率对应的尺度因子幅值减小。为了进一步说明两个参数对时变信号的聚焦作用，选取理论信号进行效果分析。该信号是由两个不同的宽频带调频信号组成，即使得高斯窗尺度因子随频率的变化范围比较大，可以有效检验方法的适用性。
![]()
图 1 理想时频谱与不同控制参数的广义S变换的时频谱a. 理想时频；b. p=0.7，λ=1对应的时频谱；c. p=0.9, λ=1对应的时频谱；d. p=1，λ=1标准S变换时频谱；e. p=1.2，λ=1对应的时频谱；f. p=1，λ=1.2对应的时频谱；g. p=1，λ=0.9对应的时频谱；h. p=1，λ=0.6对应的时频谱。Figure 1. Ideal time-frequency spectrum and time-frequency spectrum of S transform using different control factorsa. ideal time-frequency spectrum, b. p=0.7, λ=1 corresponding to time-frequency spectrum, c. p=0.9, λ=1 corresponding to time-frequency spectrum, d. p=1, λ=1 corresponding to time-frequency spectrum, e. p=1.2, λ=1 corresponding to time-frequency spectrum, f. p=1, λ=1.2 corresponding to time-frequency spectrum, g. p=1, λ=0.9 corresponding to time-frequency spectrum, h. p=1, λ=0.6 corresponding to time-frequency spectrum.$$\begin{split} y=&{\sin}\left\{3*\left[140{{\text π} }t+40{\sin}\left(3{{\text π} }t\right)\right]\right\}+\\&{\sin}\left\{3*\left[140{{\text π} }t+40{\cos}\left(3{{\text π} }t+120\right)\right]\right\} \end{split}$$ (4) 采用不同控制参数λ和p对上述信号进行广义S变换，分析对应的时频谱聚焦程度。当p值由小变大时，信号时频谱在低频端与高频端的聚焦程度均响应明显。其中低频端的聚焦程度随p值增大而变好，高频端随p值增大而变差，甚至当p＞1时，高频端出现严重失焦（图1a-d）。当p值由小变大时，信号时频谱在低频端的聚焦程度无响应，而高频端的聚焦程度也变化不大（图1c、f、g、h）。广义S变换中参数λ和p只能取固定值，其单一性的变化趋势不能兼顾高低频端的信号聚焦程度。综合以上实验结果可知，p值对时频域聚焦程度影响更大。改进广义S变换主要是更改p值变化趋势，而固定λ=1。
p值由小变大时，低频端与高频端聚焦程度响应不同。高频端信号需要小的p值，而低频端信号需要大的p值。为实现广义S变换在时频域的宽频信号扫描，将参数p改为频率的线性函数，即
$$ p=p\left(f\right)=a+bf $$ (5) 其中，初始值a＞0，变化率b＜0。
在S变换计算过程中，计算的最小频率为0 Hz，最大频率为待分析信号的Nyquist频率，在这个频带范围内规定p值线性递减，同时调整p值的初始值a和变化率b，使p值能够自动匹配信号，增加信号时频分析的聚焦程度。
为了检验该方法的效果，以理论模拟信号为例进行时频分析对比。该信号是由两个频率变化趋势相反的线性调频信号和一个正弦调频信号组成，见公式（6）。图2是标准S变换、广义S变换的优选方案（p=0.8，λ=1）和改进广义S变换的时频谱图（p=0→1，λ=1）。由图2可知，标准S变换在频率方向出现了条带状能量团，模糊了真实时频谱。广义S变换改善了时频谱图，增强了时频谱的聚焦度，而改进的广义S变换其高频的线性调频信号时频谱聚焦度更高，正弦型调频信号能量分布更均匀，分析效果要优于广义S变换。
![]()
图 2 合成信号时频谱图a. 标准S变换，b. 广义S变换（p=0.8，λ=1），c. 改进的广义S变换（p=0→1，λ=1）。Figure 2. Synthetic signal time-frequency spectruma. the standard S transform, b. conventional generalized S transform (p=0.8, λ=1), c. improved generalized S transform (p=0→1, λ=1).$$\begin{split} y=&{\cos}\left(68{{\text π} }t-20{{\text π} }{t}^{2}\right)+{\cos}\left[2{{\text π} }{\sin}\left(5{{\text π} }t\right)+120{{\text π} }t\right]+\\&{\cos}(168{{\text π} }t+28{{\text π} }{t}^{2}) \end{split}$$ (6) 为了进一步检验改进的广义S变换在地震信号分析中的适用性，选取一道添加高斯白噪声的实际地震信号进行分析。在高频噪声存在的情况下，利用上述三种方法得到时频谱的能量分布（图3）。由图3中立体图与平面图对比可知，标准S变换对低频部分的信号分析结果聚焦度比较好，但其高频噪音的时频谱的能量被过分放大，如果用这种方法在时频域采用阈值滤波的方法进行去噪，显然会把部分信号当成噪音同时也无法把高频噪音去掉。广义S变换的时频谱改善了高频噪音部分的聚焦度，但在低频端能量团几乎连在一起，时间分辨率变差。改进的广义S变换和标准S变换在低频端的能量分布相近，在高频端使高频噪音的能量分散聚焦，而且各个时频点的能量比较稳定，没有被过分放大。可以看出改进的广义S变换对地震资料进行分析或者时频域滤波，效果显然要优。
![]()
图 3 含随机噪声的地震信号时频谱图a. 标准S变换，b. 广义S变换（p=0.8, λ=1），c. 改进的广义S变换（p=0→1, λ=1）。Figure 3. Time-frequency spectrum of seismic signal with random noisea. the standard S transform, b. conventional generalized S transform (p=0.8, λ=1), c. improved generalized S transform (p=0→1, λ=1) .2.2 改进S域时频滤波
由于广义S变换具有逆变换，因此，可以利用广义S正反变换实现时频滤波。其常规滤波思路是利用二维滤波函数F(τ，f )与S变换时频谱相乘，对乘积结果沿时间轴积分，再反傅氏变换回时间域。滤波公式为：
$$ {u}_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}1}\left(t\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{S}(\tau ,f){F}(\tau ,f){\mathrm{e}}^{i2\mathrm{{\text π} }ft}\mathrm{d}\tau \mathrm{d}f $$ (7) 式中，F(τ, f )是时频域滤波函数。通过计算发现当F(τ, f ) =1时，即不对时频谱作任何处理可以完全重构信号，但当F(τ, f ) ≠1时，实际滤波结果和理想滤波结果存在差异，无法保证时频滤波的准确性[10]，如图4所示，在时频域将合成信号为500～600 ms的时频谱滤掉，反变换回时间域就出现了能量泄露。
![]()
图 4 标准S逆变换时频滤波效果图a. 合成信号，b. 合成信号时频域滤波，c. 时间域滤波效果。Figure 4. Effect of time and frequency filtering of standard S inverse transforma. synthetic signal, b. time and frequency filtering of synthetic signal, c. filtering effect of time field.为了解决这个问题，需要修正变换公式得到精确滤波的改进S域时频滤波公式。
$$\begin{split} S\left(\tau ,f\right)=&{\int }_{-\infty }^{\infty }u\left(t\right)w\left(\tau -t,f\right){\mathrm{e}}^{-i2\mathrm{{\text π} }ft}\mathrm{d}t=\\&{\int }_{-\infty }^{\infty }u\left(t\right)\frac{\lambda {\left|f\right|}^{p}}{\sqrt{2\mathrm{{\text π} }}}{\mathrm{e}}^{\frac{-{\lambda }^{2}{f}^{2p}{(\tau -t)}^{2}}{2}}{\mathrm{e}}^{-i2\mathrm{{\text π} }ft}\mathrm{d}t\end{split}$$ (8) 式中，u(t)是待分析信号，w(τ-t, f)是窗函数。
根据高斯窗函数的表达式，引入一个新的变量x(τ, t)。
$$ x\left(\tau ,t\right)=u\left(t\right){\mathrm{e}}^{\frac{-{\lambda }^{2}{f}^{2p}{(\tau -t)}^{2}}{2}} $$ 对式（8）针对变量t做傅里叶变换：
$$ x\left(\tau ,f\right)={\int }_{-\infty }^{\infty }u\left(t\right){{\mathrm{e}}^{\frac{-{\lambda }^{2}{f}^{2p}{(\tau -t)}^{2}}{2}}\mathrm{e}}^{-i2\mathrm{{\text π} }ft}\mathrm{d}t $$ (9) 对比式（7）和式（9）可得
$$ x\left(\tau ,f\right)=\frac{\sqrt{2\mathrm{{\text π} }}}{\lambda {\left|f\right|}^{p}}S\left(\tau ,f\right) $$ (10) 对式（10）针对变量 f 作反傅里叶变换：
$$ x\left(\tau ,t\right)=\frac{\sqrt{2\mathrm{{\text π} }}}{\lambda }{\int }_{-\infty }^{\infty }\frac{S\left(\tau ,f\right)}{{\left|f\right|}^{p}}{\mathrm{e}}^{i2\mathrm{{\text π} }ft}\mathrm{d}f $$ (11) 由式（8）可知，当τ=t时，u(t)和x(τ, t)之间具有对应关系：
$$ u\left(t\right)=x(t,t) $$ (12) 因此，令τ=t代入式（11）可得：
$$ u\left(t\right)=x\left(t,t\right)=\frac{\sqrt{2\mathrm{{\text π} }}}{\lambda }{\int }_{-\infty }^{\infty }\frac{S\left(t,f\right)}{{\left|f\right|}^{p}}{\mathrm{e}}^{i2\mathrm{{\text π} }ft}\mathrm{d}f $$ (13) 对u(t)进一步展开：
$$ \begin{split}u\left(t\right)=&\frac{\sqrt{2\mathrm{{\text π} }}}{\lambda }{\int }_{-\infty }^{\infty }\frac{S\left(t,f\right)}{{\left|f\right|}^{p}}{\mathrm{e}}^{i2\mathrm{{\text π} }ft}\mathrm{d}f=\\&{\int }_{-\infty }^{\infty }u\left(t\right){\mathrm{e}}^{\frac{-{\lambda }^{2}{f}^{2p}{\left(\tau -t\right)}^{2}}{2}}{\mathrm{e}}^{-i2\mathrm{{\text π} }ft}\mathrm{d}t=\\&{\int }_{-\infty }^{\infty }u\left(\tau \right){\int }_{-\infty }^{\infty }{\mathrm{e}}^{\frac{-{\lambda }^{2}{f}^{2p}{\left(t-\tau \right)}^{2}}{2}}{\mathrm{e}}^{-i2\mathrm{{\text π} }f(t-\tau )}\mathrm{d}f\mathrm{d}\tau =\\&{\int }_{-\infty }^{\infty }u\left(\tau \right)m\left(t-\tau \right)\mathrm{d}\tau =u\left(t\right)\otimes m\left(t\right)\end{split} $$ (14) 式中，
$ \otimes $ 代表褶积，函数m(t)的表达式：$$ m\left(t\right)={\int }_{-\infty }^{\infty }{\mathrm{e}}^{\frac{-{\lambda }^{2}{f}^{2p}{t}^{2}}{2}}{\mathrm{e}}^{i2\mathrm{{\text π} }ft}\mathrm{d}f $$ (15) 由式（14）可知，计算得到的结果是原始信号和信号m(t)的褶积，因此在时频域滤波结果的基础上需要再做一步滤波修正处理，最终的滤波表达式为：
$$ {u}_{filt2}\left(t\right)=\frac{\sqrt{2\mathrm{{\text π} }}}{\lambda }{\int }_{-\infty }^{\infty }\frac{S(t,f)F(t,f)}{{\left|f\right|}^{p}}{\mathrm{e}}^{i2\mathrm{{\text π} }ft}\mathrm{d}f $$ (16) $$ {u}_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}3}\left(t\right)={\rm{IFT}}\left(\frac{{U}_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}2}\left(f\right)}{M\left(f\right)}\right) $$ (17) 式中，F(t, f)是时频域滤波函数，Ufilt2(f)是ufilt2(t)的频谱，M(f)是m(t)的频谱，IFT表示反傅里叶变换。式（16）和式（17）是最终的滤波公式。
为了检验对S逆变换的改进效果，分别用标准逆变换、改进逆变换将图4b中的时频谱逆变换，并计算与准确滤波结果的差值，如图5所示。对比结果显示，改进逆变换消除了滤波区信号的畸变，避免产生滤波噪音。
![]()
图 5 准确滤波结果和不同滤波方法计算的差值a. 准确滤波结果，b. 标准逆变换计算差值（红色）和改进逆变换（蓝色）计算差值。Figure 5. Accurate filtering result and difference calculated by different filtering methodsa. accurate filtering result, b. difference calculated by standard S inverse transform (red) and difference calculated by improved S inverse transform (blue).基于上述改进广义S变换和修正的S逆变换，可以将随机噪音压制概括为3步：① 对含噪信号进行改进广义S变换得到信号的S谱；② 在S谱的基础上利用谱比法[20]计算信号的瞬时信噪比；③ 根据瞬时信噪比的不同，采用指数衰减和阈值滤波两种策略压制随机噪音。具体处理步骤如下：
（1）计算信号的S变换时频谱，利用该时频谱计算瞬时信噪比和阈值。阈值的计算思路是：计算初至前两个频率段内噪音的时频谱的平均值，作为初始阈值，具体的频率段可以分成有效频带内和有效频带外两段，计算两个阈值。由于高频随机干扰的时频谱幅值的均值随时间变化不大，而相对浅层数据深层数据的高频成分衰减快，能量弱，高频噪音能量占优，因此在无法利用初至前记录计算阈值时也可利用深层数据较高频段的时频谱计算初始阈值。
$$ {E}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}\left(t,f\right)=\frac{1}{T\times F}\sum _{t={t}_{1}}^{{t}_{2}}\sum _{f={f}_{1}}^{{f}_{2}}\left|S(t,f)\right| $$ (18) 式中，Emean(t, f)是阈值，S(t, f)是时频谱，T是参与计算时间点个数，F是参与计算频率点个数，t1到t2是参与计算的时间段，f1到f2是参与计算的频率段。
（2）实际地震数据需要考虑地层的吸收衰减，且高频衰减更快，因此深部有效频带变窄，有效信号能量弱[21]，此时如果将深部地震记录按照阈值处理，会损失很多有效信号，因此为了保留一部分有效信号以供后续处理和进一步使用，此时对瞬时信噪比低的数据段采用指数衰减的方法处理，即对信噪比小于1的时间点，对该时间点大于有效频带高频端的S谱的幅值进行一个指数衰减的加权，即将S(t, f)乘以一个以f为变量的指数衰减函数H(f)，如式（19）：
$$ H\left(f\right)={\mathrm{e}}^{-\frac{f}{\mu }} $$ (19) 式中，μ是一个衰减系数，f是频率，μ越大对高频衰减越小，反之对高频衰减越大。
（3）当瞬时信噪比大于1时，有效信号能量占优，且随机噪音的时频谱分布在整个频带上，对该时间点所有S谱采用阈值滤波法，当某频率点的幅值小于r倍的Emean(t, f)的时候，定义该点的S谱为噪音，将其充零，当其幅值大于r倍的Emean(t, f)的时候，将其时频谱的幅值减去r倍的Emean(t, f)，并将处理之后的时频谱反变换回时间域。
在实际应用中，应根据实际地震资料的情况，进行反复试验，选取合适的μ和r值，既能压制随机噪音，又能保护高频端的有效信号，为数据拓频留有空间。
3. 合成信号试验
为了检验方法的有效性，首先利用零相位雷克子波模拟48道经地层吸收衰减的地震记录，加入随机白噪声后，利用改进广义S变换对地震记录压制随机噪音（图6）。抽取单道地震模拟数据对比，能够清晰地看出改进广义S变换压制随机噪声的效果，尤其深部低信噪比信号也得到有效的恢复（图7）。分析时频域中滤波效果，可看到有效信号时频谱得以保留，随机噪音时频谱得到有效压制（图8）。
![]()
图 6 含噪地震记录去噪效果图a. 48道模拟地震记录， b. 含白噪声的模拟地震记录， c. 去除噪声的模拟地震记录。Figure 6. Denoising effect for seismic records with noisea. 48 channels simulated seismic record, b. simulated seismic record with white noise, c. simulated seismic record after denoising.![]()
图 7 单道信号对比图a. 加白噪声后与未加噪声单道信号对比， b. 去噪后与未加噪声单道信号对比。Figure 7. Comparison of single channel signalsa. comparison of single channel signals with noise and those without noise, b. comparison of single channel signals without noise and those after noise reduction.![]()
图 8 时频域滤波效果对比a. 不含白噪声模拟地震道的时频谱，b. 含白噪声模拟地震道的时频谱，c. 去除噪声模拟地震道的时频谱。Figure 8. Comparison of filtering effects in time-frequency domaina. time and frequency spectrum of simulated seismic channel without noise, b. time and frequency spectrum of simulated seismic channel with white noise, c. time and frequency spectrum of simulated seismic channel after noise reduction.4. 实际资料处理
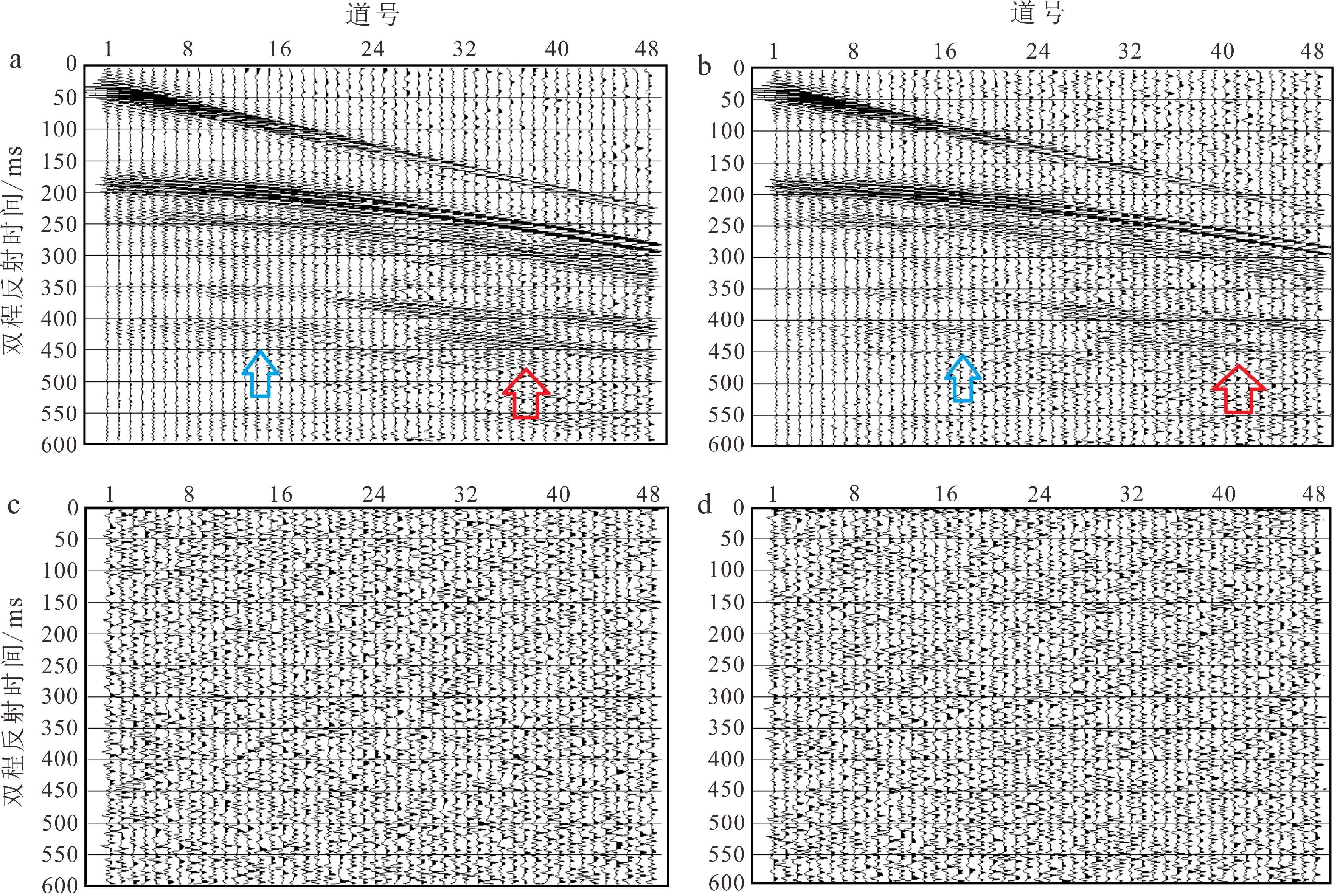
为了检验本文改进的广义S变换方法在实际资料中的应用效果，选择高分辨率海洋二维地震叠前剖面进行去噪处理，并将其与传统广义S变换滤波去噪法进行对比。本文首先通过单炮初至前的噪声信号确定去噪阈值，再利用改进的广义S变换进行时频滤波。图9为地震叠前单炮剖面。传统广义S变换参数经过对比后确定为（p=0.6, λ=1），改进后的广义S变换应用参数（p=0.6→1, λ=1）。图10是两种方法压制噪声效果图。从整体上可以看出，两种广义S变换时频域去噪均能达到一定效果，随机噪声得到合理去除。但改进的广义S变换在远偏移距处的弱信号去噪效果更好，深部反射同相轴连续性更优，有效信号的损失较小，对弱信号起到保护作用。
![]()
图 10 两种方法压制噪声效果对比a. 改进广义S变换压噪后剖面，b. 传统广义S变换压噪后剖面，c. 改进广义S变换去除的噪声，d. 传统广义S变换去除的噪声。Figure 10. Comparison of noise suppression effects between two methodsa. denoised profile by improved generalized S transform, b. denoised profile by traditional generalized S transform, c. noise removal by improved generalized S transform, d. noise removal by generalized S transform.5. 结论
本文针对广义S变换高斯窗参数λ和p固定、逆变换存在信号泄露的问题，提出了改进的思路和计算过程，并将其应用于随机噪音压制。通过对合成信号和实际资料的应用，得到以下认识：
（1）改进广义S变换时频谱聚焦度要优于广义S变换，而且参数p与频率f呈线性变化，以适应不同的应用目的；改进后的逆变换可以实现精确滤波，消除了滤波噪音。
（2）利用单炮初至前或深部较高频段时频谱计算阈值，根据每个时刻时频谱的幅值与阈值的差异压制噪音，同时考虑到地震信号的有效频带和瞬时信噪比随时间变化的情况，对瞬时信噪比较低的采用指数衰减的策略压制噪音，可以在保护有效信号的基础上实现去噪目的。
（3）高斯窗参数
$ p $ 的范围选择，应当根据高低频端的聚焦程度而改变。通过试验确定的参数$ p $ ，既能够有效压制噪音又能避免弱有效信号的损失，为后续处理打好基础。 -
![]()
图 1 理想时频谱与不同控制参数的广义S变换的时频谱
a. 理想时频；b. p=0.7，λ=1对应的时频谱；c. p=0.9, λ=1对应的时频谱；d. p=1，λ=1标准S变换时频谱；e. p=1.2，λ=1对应的时频谱；f. p=1，λ=1.2对应的时频谱；g. p=1，λ=0.9对应的时频谱；h. p=1，λ=0.6对应的时频谱。
Figure 1. Ideal time-frequency spectrum and time-frequency spectrum of S transform using different control factors
a. ideal time-frequency spectrum, b. p=0.7, λ=1 corresponding to time-frequency spectrum, c. p=0.9, λ=1 corresponding to time-frequency spectrum, d. p=1, λ=1 corresponding to time-frequency spectrum, e. p=1.2, λ=1 corresponding to time-frequency spectrum, f. p=1, λ=1.2 corresponding to time-frequency spectrum, g. p=1, λ=0.9 corresponding to time-frequency spectrum, h. p=1, λ=0.6 corresponding to time-frequency spectrum.
![]()
图 2 合成信号时频谱图
a. 标准S变换，b. 广义S变换（p=0.8，λ=1），c. 改进的广义S变换（p=0→1，λ=1）。
Figure 2. Synthetic signal time-frequency spectrum
a. the standard S transform, b. conventional generalized S transform (p=0.8, λ=1), c. improved generalized S transform (p=0→1, λ=1).
![]()
图 3 含随机噪声的地震信号时频谱图
a. 标准S变换，b. 广义S变换（p=0.8, λ=1），c. 改进的广义S变换（p=0→1, λ=1）。
Figure 3. Time-frequency spectrum of seismic signal with random noise
a. the standard S transform, b. conventional generalized S transform (p=0.8, λ=1), c. improved generalized S transform (p=0→1, λ=1) .
![]()
图 4 标准S逆变换时频滤波效果图
a. 合成信号，b. 合成信号时频域滤波，c. 时间域滤波效果。
Figure 4. Effect of time and frequency filtering of standard S inverse transform
a. synthetic signal, b. time and frequency filtering of synthetic signal, c. filtering effect of time field.
![]()
图 5 准确滤波结果和不同滤波方法计算的差值
a. 准确滤波结果，b. 标准逆变换计算差值（红色）和改进逆变换（蓝色）计算差值。
Figure 5. Accurate filtering result and difference calculated by different filtering methods
a. accurate filtering result, b. difference calculated by standard S inverse transform (red) and difference calculated by improved S inverse transform (blue).
![]()
图 6 含噪地震记录去噪效果图
a. 48道模拟地震记录， b. 含白噪声的模拟地震记录， c. 去除噪声的模拟地震记录。
Figure 6. Denoising effect for seismic records with noise
a. 48 channels simulated seismic record, b. simulated seismic record with white noise, c. simulated seismic record after denoising.
![]()
图 7 单道信号对比图
a. 加白噪声后与未加噪声单道信号对比， b. 去噪后与未加噪声单道信号对比。
Figure 7. Comparison of single channel signals
a. comparison of single channel signals with noise and those without noise, b. comparison of single channel signals without noise and those after noise reduction.
![]()
图 8 时频域滤波效果对比
a. 不含白噪声模拟地震道的时频谱，b. 含白噪声模拟地震道的时频谱，c. 去除噪声模拟地震道的时频谱。
Figure 8. Comparison of filtering effects in time-frequency domain
a. time and frequency spectrum of simulated seismic channel without noise, b. time and frequency spectrum of simulated seismic channel with white noise, c. time and frequency spectrum of simulated seismic channel after noise reduction.
![]()
图 10 两种方法压制噪声效果对比
a. 改进广义S变换压噪后剖面，b. 传统广义S变换压噪后剖面，c. 改进广义S变换去除的噪声，d. 传统广义S变换去除的噪声。
Figure 10. Comparison of noise suppression effects between two methods
a. denoised profile by improved generalized S transform, b. denoised profile by traditional generalized S transform, c. noise removal by improved generalized S transform, d. noise removal by generalized S transform.
-
[1] Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform [J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. doi: 10.1109/78.492555
[2] 付勋勋, 徐峰, 秦启荣, 等. 基于改进的广义S变换求取地层品质因子Q值[J]. 石油地球物理勘探, 2012, 47(3):457-461 FU Xunxun, XU Feng, QIN Qirong, et al. Estimation of quality factor based on improved generalized S-transform [J]. Oil Geophysical Prospecting, 2012, 47(3): 457-461.
[3] 吴淑玉, 刘俊. 时频分析在北黄海东部坳陷中生界储层的应用[J]. 海洋地质与第四纪地质, 2016, 36(1): 189-196 WU Shuyu, LIU Jun. Application of time-frequency analysis to the Mesozoic reservoir, eastern depression of North Yellow Sea[J], 2016, 36(1): 189-196.
[4] Pinnegar C R, Mansinha L. The S-transform with windows of arbitrary and varying shape [J]. Geophysics, 2003, 68(1): 381-385. doi: 10.1190/1.1543223
[5] 陈学华, 贺振华, 黄德济. 广义S变换及其时频滤波[J]. 信号处理, 2008, 24(1):28-31 doi: 10.3969/j.issn.1003-0530.2008.01.007 CHEN Xuehua, HE Zhenhua, HUANG Deji. Generalized S transform and its time-frequency filtering [J]. Signal Processing, 2008, 24(1): 28-31. doi: 10.3969/j.issn.1003-0530.2008.01.007
[6] 高静怀, 陈文超, 李幼铭, 等. 广义S变换与薄互层地震响应分析[J]. 地球物理学报, 2003, 46(4):526-532 doi: 10.3321/j.issn:0001-5733.2003.04.015 GAO Jinghuai, CHEN Wenchao, LI Youming, et al. Generalized S transform and seismic response analysis of thin interbeds [J]. Chinese Journal of Geophysics, 2003, 46(4): 526-532. doi: 10.3321/j.issn:0001-5733.2003.04.015
[7] Radad M, Gholami A, Siahkoohi H R. S-transform with maximum energy concentration: Application to non-stationary seismic deconvolution [J]. Journal of Applied Geophysics, 2015, 118: 155-166. doi: 10.1016/j.jappgeo.2015.04.010
[8] 周竹生, 刘冰. 基于含可变因子S变换的面波压制技术[J]. 物探化探计算技术, 2013, 35(5):555-560 doi: 10.3969/j.issn.1001-1749.2013.05.11 ZHOU Zhusheng, LIU Bing. Surface wave suppression technology based on S-transform with variable factor [J]. Computing Techniques for Geophysical and Geochemical Exploration, 2013, 35(5): 555-560. doi: 10.3969/j.issn.1001-1749.2013.05.11
[9] 黄捍东, 冯娜, 王彦超, 等. 广义S变换地震高分辨率处理方法研究[J]. 石油地球物理勘探, 2014, 49(1):82-88 HUANG Handong, FENG Na, WANG Yanchao, et al. High-resolution seismic processing based on generalized S transform [J]. Oil Geophysical Prospecting, 2014, 49(1): 82-88.
[10] 张固澜, 熊晓军, 容娇君, 等. 基于改进的广义S变换的地层吸收衰减补偿[J]. 石油地球物理勘探, 2010, 45(4):512-515 ZHANG Gulan, XIONG Xiaojun, RONG Jiaojun, et al. Stratum absorption and attenuation compensation based on improved generalized S-transform [J]. Oil Geophysical Prospecting, 2010, 45(4): 512-515.
[11] 陈学华, 贺振华, 黄德济, 等. 时频域油气储层低频阴影检测[J]. 地球物理学报, 2009, 52(1):215-221 CHEN Xuehua, HE Zhenhua, HUANG Deji, et al. Low frequency shadow detection of gas reservoirs in time-frequency domain [J]. Chinese Journal of Geophysics, 2009, 52(1): 215-221.
[12] Yu Z, McMechan G A, Ferguson J F, et al. Adaptive wavelet filtering of seismic data in the wavelet transform domain [J]. Journal of Seismic Exploration, 2002, 11(3): 223-246.
[13] 赵淑红, 朱光明. S变换时频滤波去噪方法[J]. 石油地球物理勘探, 2007, 42(4):402-406 doi: 10.3321/j.issn:1000-7210.2007.04.008 ZHAO Shuhong, ZHU Guangming. Time-frequency filtering to denoise by S transform [J]. Oil Geophysical Prospecting, 2007, 42(4): 402-406. doi: 10.3321/j.issn:1000-7210.2007.04.008
[14] 李雪英, 侯相辉. 基于广义S变换的叠前高频噪声压制[J]. 石油地球物理勘探, 2011, 46(4):545-549 LI Xueying, HOU Xianghui. Prestack high frequency noise suppression based on generalized S transform [J]. Oil Geophysical Prospecting, 2011, 46(4): 545-549.
[15] 王云专, 兰金涛, 龙玉沙. 基于S变换的随机噪声压制方法[J]. 地球物理学进展, 2010, 25(2):562-567 doi: 10.3969/j.issn.1004-2903.2010.02.026 WANG Yunzhuan, LAN Jintao, LONG Yusha. The method for attenuating random noise based on S transform [J]. Progress in Geophysics, 2010, 25(2): 562-567. doi: 10.3969/j.issn.1004-2903.2010.02.026
[16] Schimmel M, Gallart J. The inverse S-transform in filters with time-frequency localization [J]. IEEE Transactions on Signal Processing, 2005, 53(11): 4417-4422. doi: 10.1109/TSP.2005.857065
[17] 王德营, 李振春, 王姣. S域时频滤波分析与改进[J]. 石油物探, 2015, 54(4):396-403 doi: 10.3969/j.issn.1000-1441.2015.04.005 WANG Deying, LI Zhenchun, WANG Jiao. The analysis and improvement on time-frequency filtering in S-transform domain [J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 396-403. doi: 10.3969/j.issn.1000-1441.2015.04.005
[18] Pinnegar C R. Comments on “The Inverse S-Transform in Filters With Time-Frequency Localization” [J]. IEEE Transactions on Signal Processing, 2007, 55(10): 5117-5120. doi: 10.1109/TSP.2007.896050
[19] Pei S C, Wang P W. Modified inverse s transform for filtering in time-frequency spectrum[C]//2007 IEEE International Conference on Acoustics, Speech and Signal Processing. Honolulu, HI, USA: IEEE, 2007: III-1169-III-1172.
[20] 张军华, 藏胜涛, 周振晓, 等. 地震资料信噪比定量计算及方法比较[J]. 石油地球物理勘探, 2009, 44(4):481-486 doi: 10.3321/j.issn:1000-7210.2009.04.018 ZHANG Junhua, ZANG Shengtao, ZHOU Zhenxiao, et al. Quantitative computation and comparison of S/N ratio in seismic data [J]. Oil Geophysical Prospecting, 2009, 44(4): 481-486. doi: 10.3321/j.issn:1000-7210.2009.04.018
[21] 王小杰, 颜中辉, 刘欣欣, 等. 基于小波分频的Q值补偿技术在东海中深层油气勘探中的应用[J]. 海洋地质与第四纪地质, 2019, 39(6):200-206 WANG Xiaojie, YAN Zhonghui, LIU Xinxin, et al. The application of formation Q value compensation method based on wavelet frequency division to the exploration of middle-deep hydrocarbon in the East China Sea [J]. Marine Geology & Quaternary Geology, 2019, 39(6): 200-206.
-
期刊类型引用(3)
1. 刘景良，苏杰龙，戴逸宸，李宇祖，黄永，郑文婷. 基于滑动窗宽优化的LMSSGST识别非平稳信号瞬时频率. 振动与冲击. 2024(19): 183-193 . 
百度学术
2. 李雪英，王鑫. 二阶同步提取变换的沉积旋回界面定位与追踪识别. 黑龙江科技大学学报. 2023(04): 614-621 . 百度学术
3. 吴耀乐，邓敏. 基于残差卷积神经网络的随机噪声压制网络的海洋地震资料去噪技术研究. 中国石油和化工标准与质量. 2022(22): 175-177 . 百度学术
其他类型引用(4)
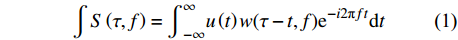
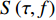
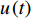
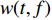
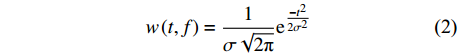
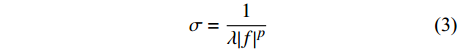
下载:
计量
- 文章访问数: 5943
- HTML全文浏览量: 501
- PDF下载量: 90
- 被引次数: 7
