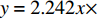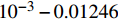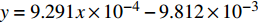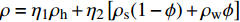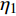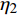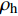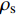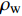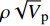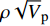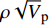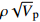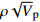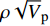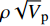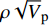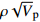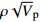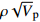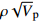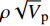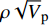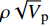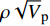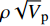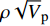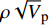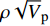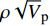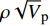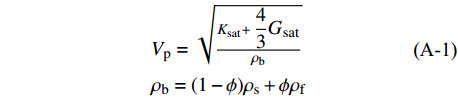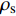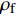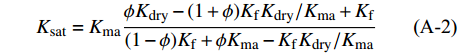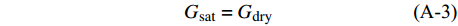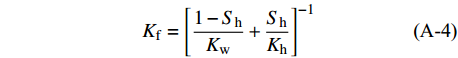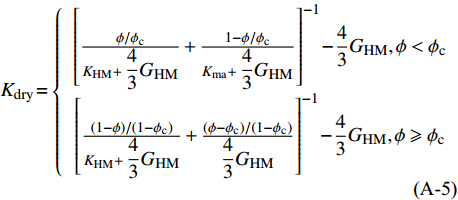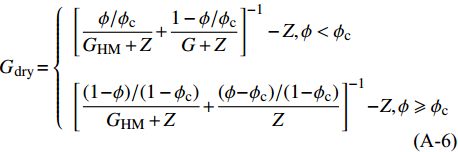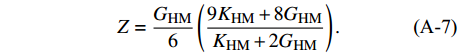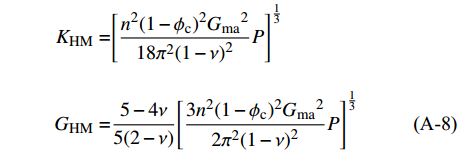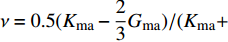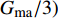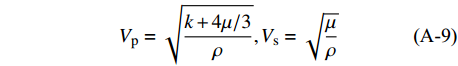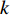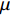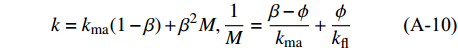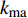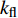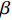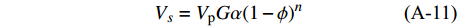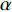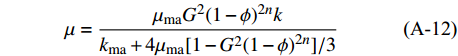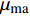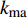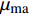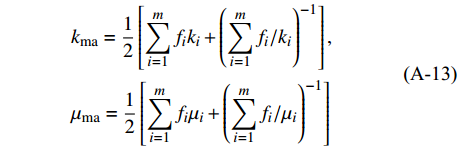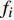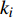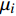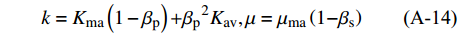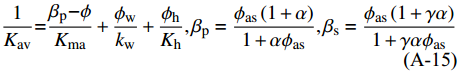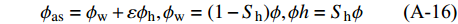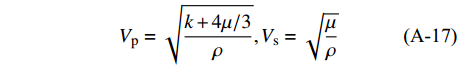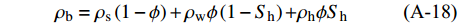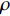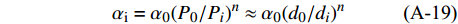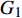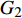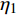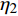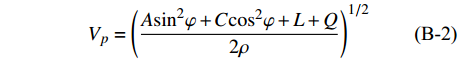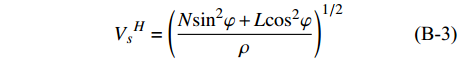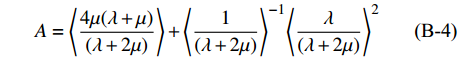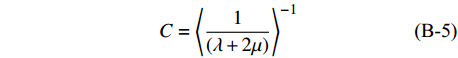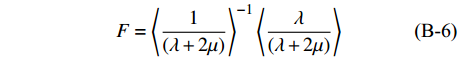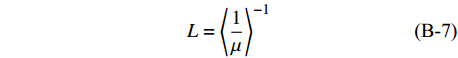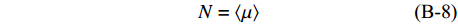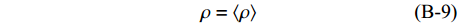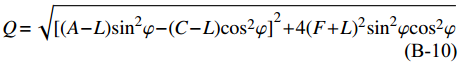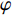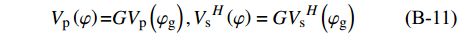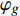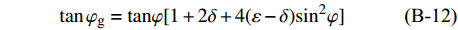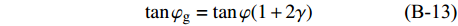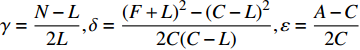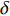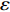Identification of pore-filling and fracture-filling hydrate by petrophysical simulation and acoustic experiment
-
摘要: 孔隙充填和裂隙充填是自然界中水合物赋存的两种基本形态，其类型判别对储量评价、钻井安全以及环境评估均具有重要影响。本文模拟南海孔隙充填和裂隙充填两种类型水合物储层，利用岩石物理模型和声学模拟实验获取声波速度和密度，对两种类型的识别方法进行了探索。结果显示，孔隙充填和裂隙充填型水合物沉积体系的纵波速度都随水合物体积分数的增大而增大，密度都随水合物体积分数增大而减小。将速度与密度参数结合计算两种类型水合物阻抗和
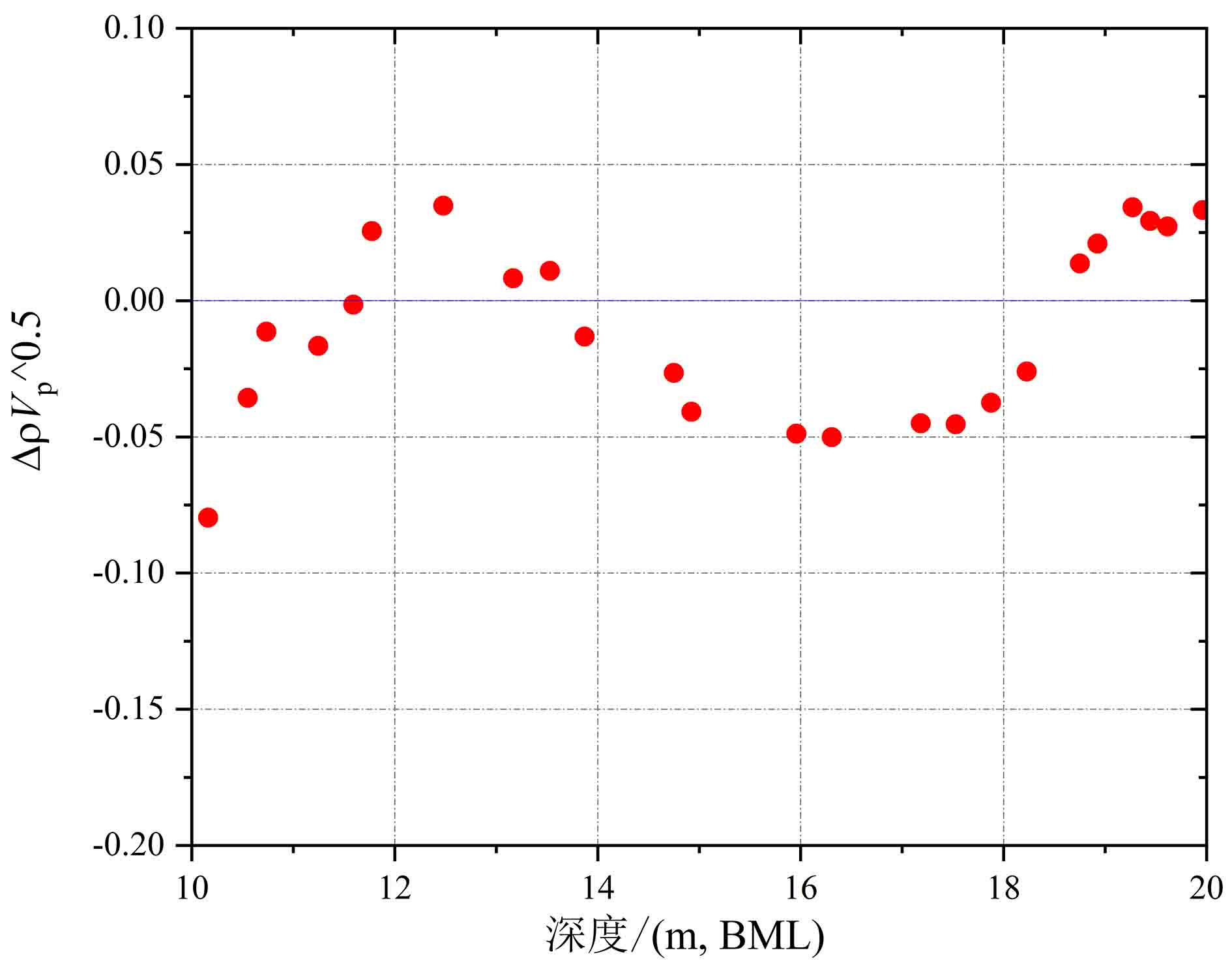
$\rho {\sqrt V _{\rm{p}}}$ 属性表明：对于含孔隙充填型水合物沉积体系的$\rho {\sqrt V _{\rm{p}}}$ 属性，岩石物理模拟的计算结果与实验结果斜率均为正；而对于含裂隙充填型水合物沉积物的$\rho {\sqrt V _{\rm{p}}}$ 属性，其斜率均为负。但当水合物体积分数小于40%时，含裂隙充填型水合物沉积物的理论计算结果与实验值存在偏差，因此，在计算低体积分数水合物的$\rho {\sqrt V _{\rm{p}}}$ 属性时，需要对模型进行适当修正。本文利用$\rho {\sqrt V _{\rm{p}}}$ 属性对GMGS2航次16井赋存的孔隙充填和裂隙充填型水合物进行了验证，结果表明井中上部分赋存的水合物以裂隙充填型为主，底部以孔隙充填型为主，验证结果与实际钻探结果一致，表明该方法用于识别水合物类型是可行的。Abstract: Pore-filling and fracture-filling are two of the basic occurrences of natural gas hydrates in nature. To discriminate the type of gas hydrate is critically important for resource assessment, drilling safety and environment evaluation. In this paper, simulation experiment was carried out for the pore-filling and fracture-filling hydrate reservoirs in the South China Sea. The acoustic velocity and density of the two kinds of hydrate are obtained by petrophysical simulation and acoustic experiment simulation. The results suggest that the P wave velocity of the depositional mediums containing pore-filling and fracture-filling hydrate tends to increase with the volume fraction of hydrate, while the density decreases. Furthermore, we tested the impedance and the$\rho {\sqrt V _{\rm{p}}}$ property of the two types of hydrate by combining velocity and density parameters together. The results also show that for the pore-filling hydrates, the properties of$\rho {\sqrt V _{\rm{p}}}$ calculated by the petrophysical models and experimental$\rho {\sqrt V _{\rm{p}}}$ both show positive slope, while The$\rho {\sqrt V _{\rm{p}}}$ property of the fracture-filling hydrate shows negative slope. However, the differences between the model and experiment results of fracture-filling hydrate are obvious when the volume fraction of gas hydrate is less than 40%. It means that the petrophysical for fracture-filling hydrate needs to be further improved. In addition, pore-filling and fracture-filling hydrate in GMGS2-16 Site has been verified by the property of$\rho {\sqrt V _{\rm{p}}}$ . The results show that the hydrate in the upper part of the well is mainly fracture-filling hydrate, as the bottom dominated by pore-filling hydrate. The verification has been confirmed by actual drilling results.-
Keywords:
- hydrate /
- pore-filling /
- fracture-filling /
- petrophysical simulation /
- acoustic experiment
-
天然气水合物主要赋存于大陆边缘和大陆永久冻土区[1-2]，以层状、块状、分散状、胶结状、瘤状等形式赋存于地层中[3]，可归结为两大类，即孔隙充填型和裂隙充填型。孔隙充填型水合物替代了孔隙中的流体，赋存于沉积物孔隙中[4]；裂隙充填型水合物则以纯水合物形式与沉积物互相接触，一般存在于沉积物裂隙、地层裂隙、断层或泥火山等特殊地质体中。因此，由于赋存状态和岩石物理性质不同，针对孔隙充填型、裂隙充填型水合物往往采用不同的方法进行资源评估。然而，在野外勘探过程中，如何通过简便的方法识别水合物类型，尚无较为成熟的识别方法。
已有钻探结果为认识孔隙充填型和裂隙充填型水合物打下了良好基础[5-6]。中国、美国、印度、韩国等钻探表明，中国南海神狐海域天然气水合物以孔隙充填为主[7]，而美国墨西哥湾[8]、韩国Ulleung盆地[9]和印度K-G盆地[10-11]的细粒沉积物中均发现了裂隙充填型水合物。2006年，印度国家天然气水合物计划（NGHP01）在K-G盆地通过测井和钻探发现大量裂隙充填型水合物富集，测井和红外成像显示水合物多呈结核状、脉状、瘤状，充填于高角度（60°～120°）裂隙以及近水平层理中，其中充填水合物的裂隙层位厚度最大可达135 m，长度达数米以上[1, 5, 11]。孔隙充填型水合物和裂隙充填型水合物最主要的区别在于非微观尺度研究中，孔隙充填型水合物通常被看作是各向同性介质，而裂隙充填型水合物则是各向异性介质[12]。中国地质调查局广州海洋地质调查局2013年在中国南海北部海域开展的第二次水合物勘探GMGS2，在13个站位布设了21个钻井，并取得了保压岩心[13]，其中5个站位发现了水合物，这一航次中同时发现了孔隙充填型和裂隙充填型水合物。
由于孔隙充填型和裂隙充填型水合物的形成机理和地球物理响应都存在差异，因此，在无钻探井位的区域，准确识别两类水合物在沉积层中的分布形态，对于水合物资源评价、钻采安全以及环境等方面都至关重要[14]。目前为止，关于孔隙充填型和裂隙充填型水合物识别的文献相对较少。戴丹青等[15]利用中观衰减理论，用斑块饱和模型和双孔隙模型针对水合物在地层中的赋存状态，研究了地震频带内BSR界面反射系数的变化特征，并将研究结果应用到存在孔隙充填型水合物的南海神狐海域和存在裂隙充填型水合物的布莱克海台，模拟结果与实际情况吻合较好。王吉亮等[3]为识别印度东海岸NGHP01-10D井的水合物赋存状态，利用等效介质理论（EMT）和层状介质横向各向异性模型分别计算了水合物的饱和度，发现层状介质横向各向异性模型计算的结果与实际情况吻合较好，且存在的裂隙多为高角度裂隙。Lee等[16]利用各向同性模型和横向各向同性理论计算了韩国东海Ulleung 盆地UBGH2-3B井中水合物层的电阻率、纵波速度和水合物饱和度，研究结果表明井中局部范围水合物的赋存类型为裂隙充填型，气烟囱上半部分（5～14 mbsf）地层中主要赋存裂隙角度约7°的裂隙充填型水合物，下半部分（45～103 mbsf）中赋存高角度裂隙充填型水合物。Liu等[17]提出利用纵波速度和电阻率交汇图的斜率来识别两类水合物。Sriram等[18]对含孔隙充填型/裂隙充填型水合物地层的BSR进行了AVA（振幅随入射角的变化）模拟，通过模拟将两者的AVA类别进行归类，从而达到水合物在储层中赋存形态的识别。Liu等[19]通过岩石物理模拟分别计算了孔隙充填型和裂隙充填型水合物的密度和速度，提出用密度速度属性识别孔隙充填型及裂隙充填型水合物的方法。
迄今为止，对水合物赋存形态识别的研究多以模拟手段为主来计算两种类型水合物储层的电阻率、纵波速度、地震衰减/反射系数及AVA/AVO属性。截至目前，未发现将模拟结果与实验实测数据进行对比分析的案例。本文针对孔隙充填型水合物选取了EMT（A、B模式）、BGTL和STPE模型，针对裂隙充填型水合物（本文仅以裂隙空间发育的纯水合物为研究对象）（图1a）选取了横向各向同性理论（TIT），模拟了两种类型水合物的密度和声波速度与水合物体积分数间的变化特征，并通过声学实验获取了孔隙充填型和裂隙充填型水合物的纵波速度特征。
![]()
图 1 裂隙充填型水合物的类型[20]a. 裂隙空间发育的纯水合物，b. 黏土质沉积物夹杂含水合物的砂质沉积介质， c. 黏土沉积物中发育连续微裂隙中的水合物，d. 黏土沉积物中不连续微裂隙中的水合物。Figure 1. Types of fracture-filling hydrates[20]a. Pure hydrate in fracture space， b. sandy sedimentary medium with hydrate in clay sediment，c. hydrate in continuous microfractures developed in clay sediments，d. hydrate in discontinuous microfractures in clay sediments.1. 天然气水合物岩石物理模型选取与计算
1.1 孔隙充填型水合物岩石物理模型选取与计算
Liu等[18]、胡高伟[21]、王吉亮等[3]等关于孔隙充填型水合物岩石物理模拟的研究结果表明，等效介质理论（EMT）、BGTL理论和简化三相方程（STPE）的计算结果与实验测试波速的吻合程度相比其他岩石物理模型更具优势。因此，本文针对孔隙充填型水合物选取了EMT-A/B、BGTL和STPE岩石物理模型，计算了含孔隙充填型水合物的南海沉积物（孔隙度为0.4）的密度和纵波速度。表1为模拟计算所用的南海沉积物的弹性参数及含量表，模型计算公式见附录。
1.2 孔隙充填型水合物模型计算结果
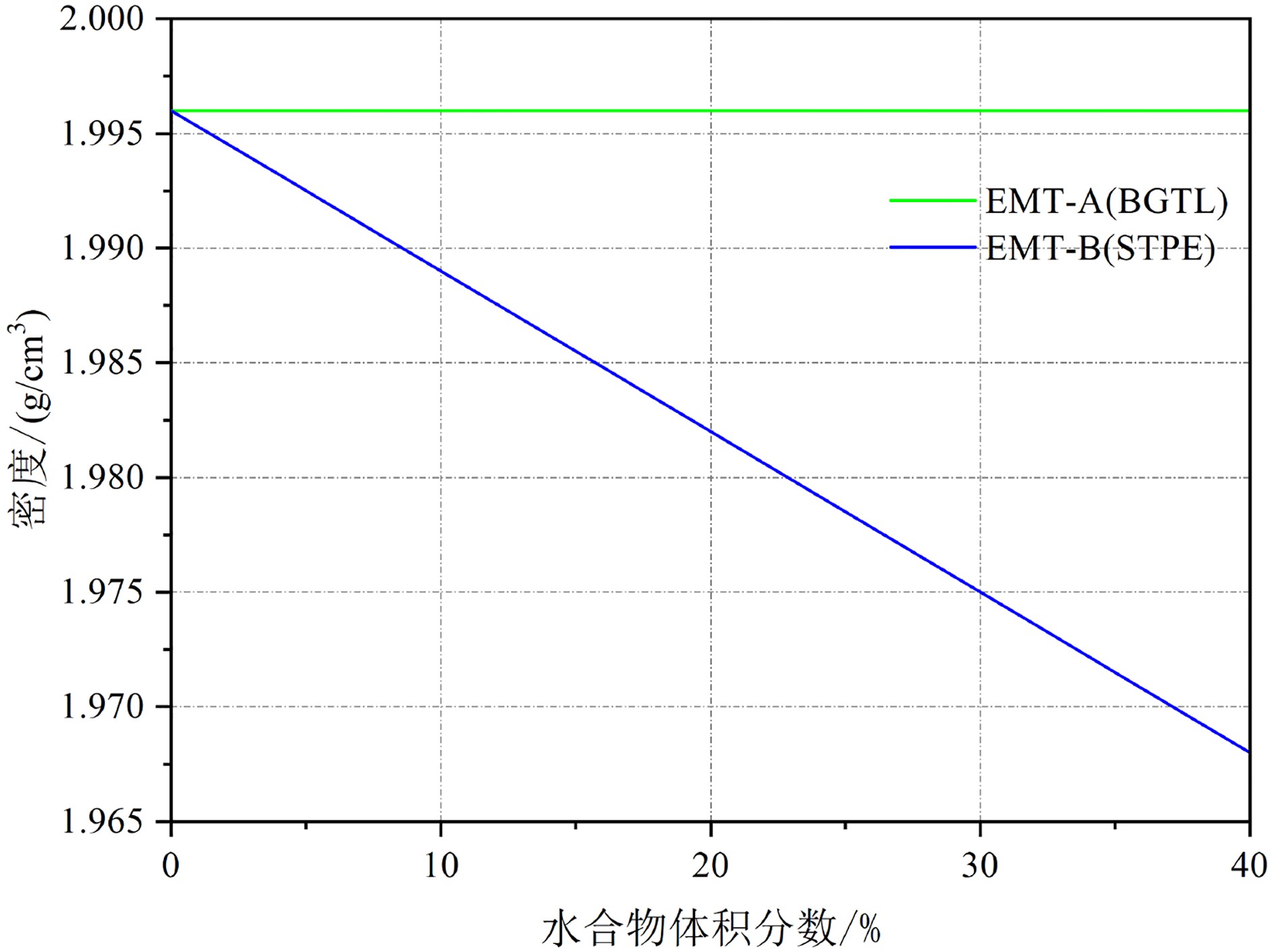
由于EMT-A和BGTL的密度计算公式相同，因此，两者模拟的密度曲线重合（图2），而EMT-B模式中，水合物形成后充当骨架的一部分，同时使得沉积物孔隙度减小，该模式计算密度时对沉积物孔隙度进行了修正，但最终计算结果与STPE相同。各模式计算的孔隙充填型水合物介质的密度尽管有差异，但最大差值仅为1.25%。
![]()
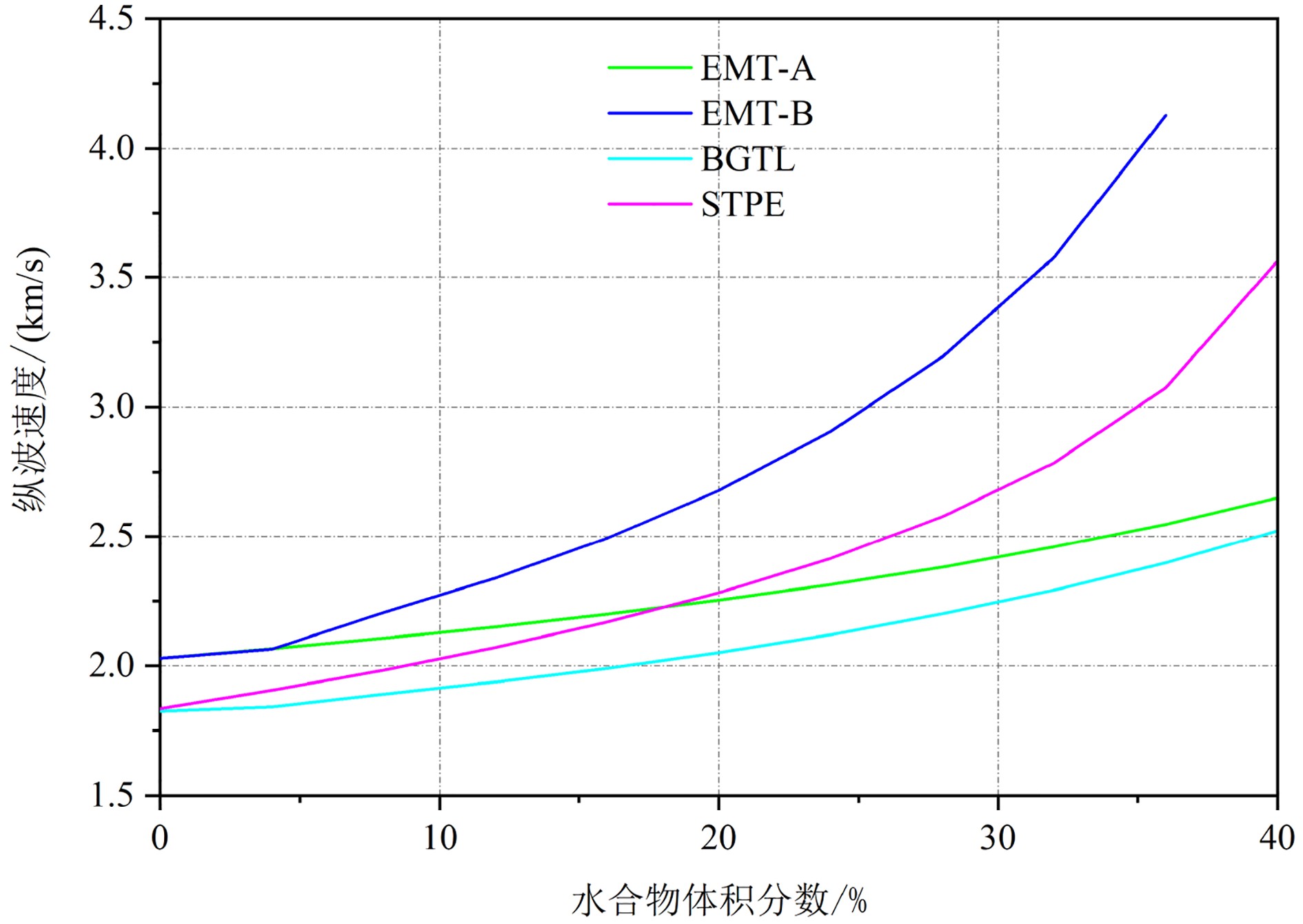
图 2 EMT、BGTL、STPE模型计算的含孔隙充填型水合物的密度Figure 2. The density of pore-filling hydrate calculated by EMT、BGTL and STPE models3类岩石物理模型计算的纵波速度均随水合物体积分数的增加而增大（图3），但不同模型的波速计算方式不同，波速初始起跳值也不同。当沉积物孔隙中未生成水合物（体积分数为0）时，EMT-A/B模式计算的沉积物纵波速度大于BGTL和STPE模型计算的波速，3类模型计算的纵波速度大小分两种情况：①当水合物体积分数小于17%时，波速大小为：EMT-B＞EMT-A＞STPE＞BGTL；②水合物体积分数大于17%时，EMT-B＞STPE＞EMT-A＞BGTL。EMT-B模式计算的波速值最大，BGTL的计算值最小，图3中横坐标体积分数40%对应水合物饱和度为100%。
![]()
图 3 EMT、BGTL、STPE模型计算的含孔隙充填型水合物的纵波速度Figure 3. The P-wave velocity of pore-filling hydrate calculated by EMT、BGTL and STPE models1.3 裂隙充填型水合物岩石物理模型与计算
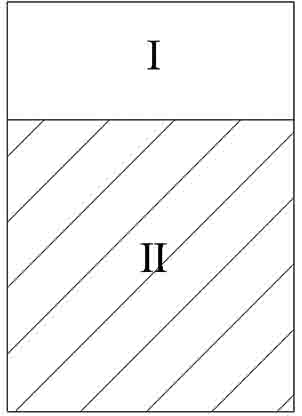
裂隙充填型水合物模型用横向各向同性理论（TIT）进行计算。模型由两个端元组成（图4），端元Ⅰ为裂隙，100%由纯水合物充填，端元Ⅱ为饱和水的南海沉积物（泥质黏土，孔隙度为0.4），其弹性参数及含量见表1。端元Ⅱ的体积模量和剪切模量基于Hill平均方程（B-5）和STPE模型计算。
![]()
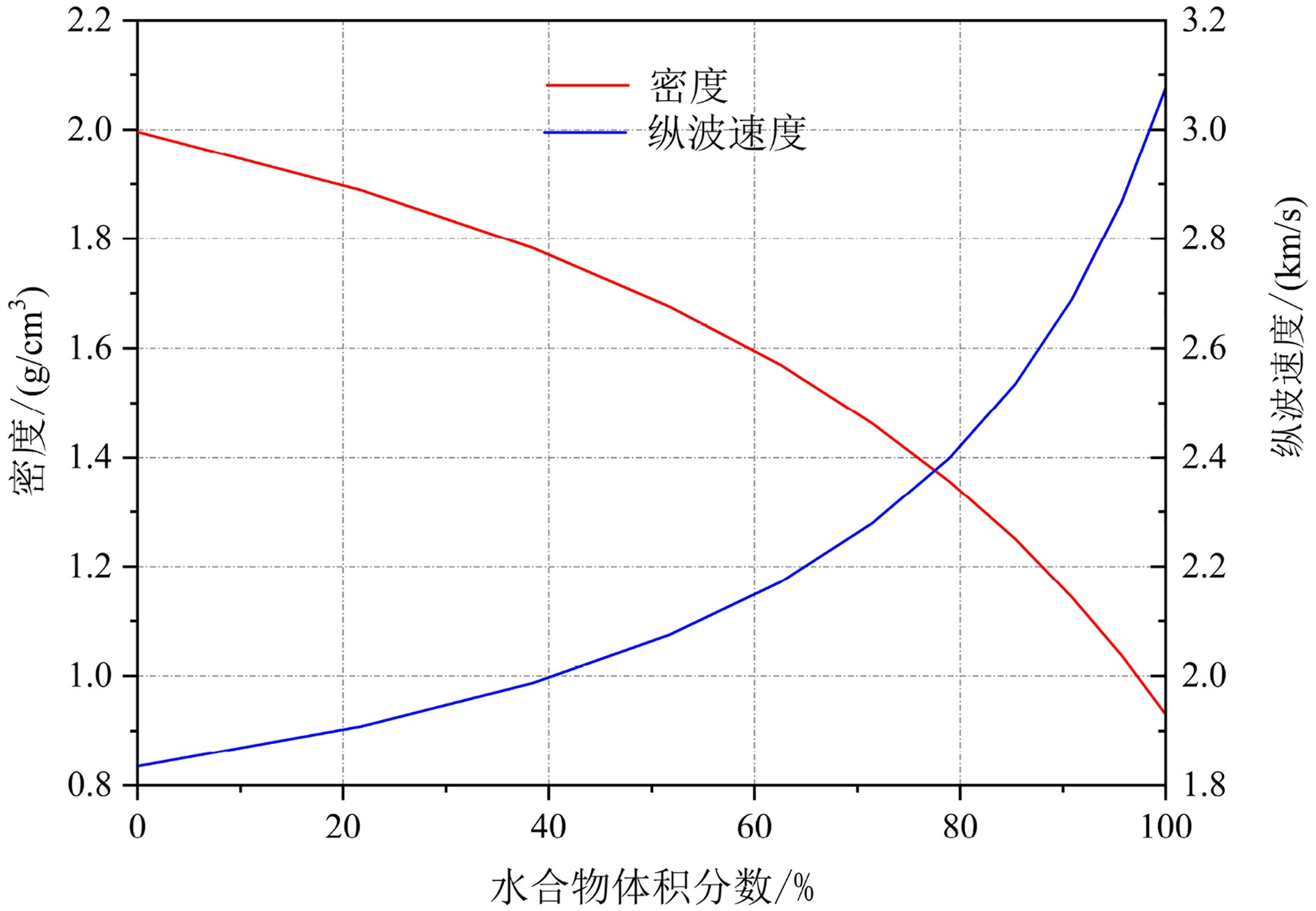
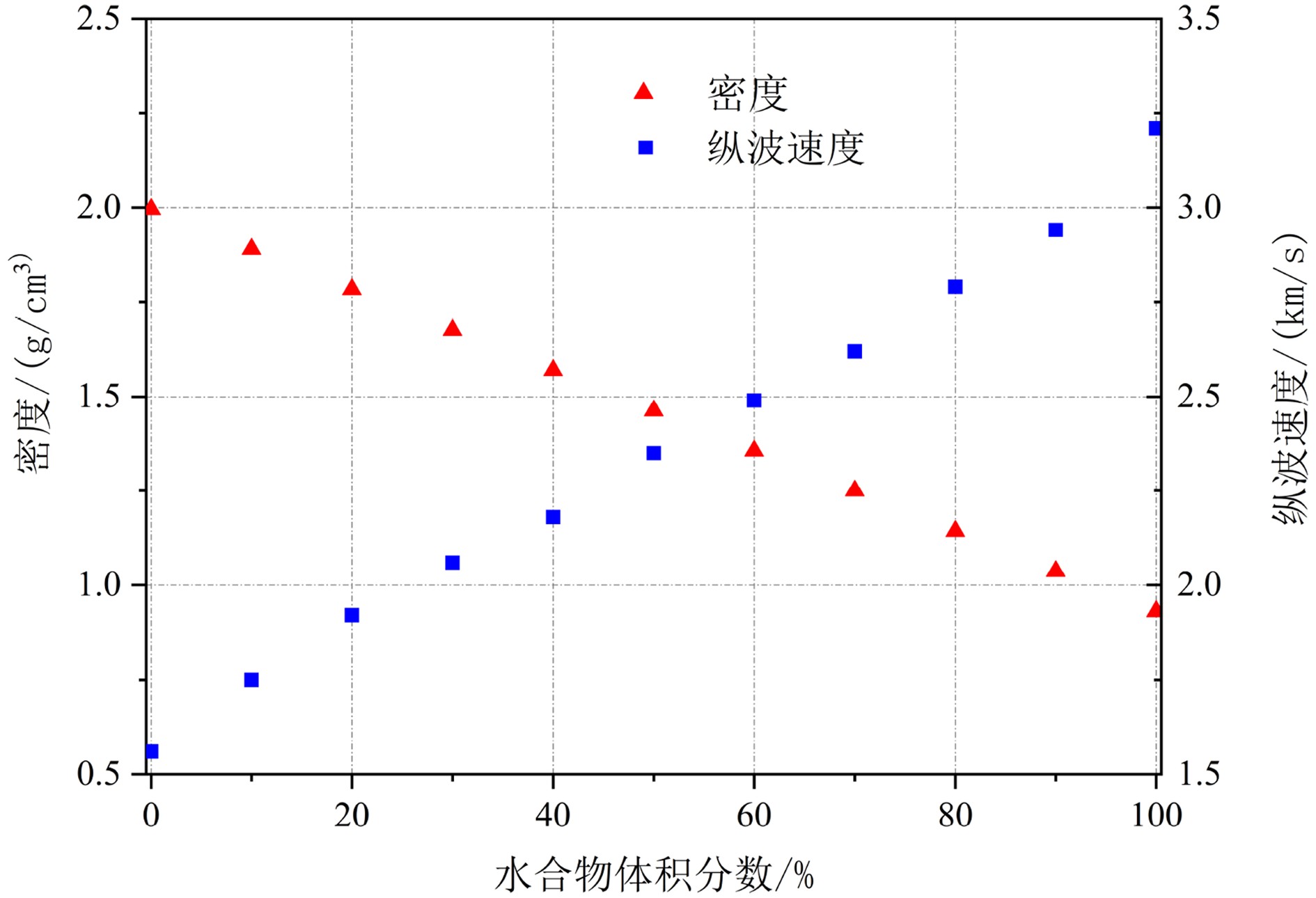
由横向各向同性理论计算的含裂隙充填型水合物的南海沉积介质的密度和纵波速度结果（图5）发现，随着水合物体积分数增大，沉积介质的总密度减小，且当模型中端元Ⅰ占比为100%时，裂隙中为纯水合物，此时介质密度最小，水合物的密度为0.93 g/cm3；纵波速度曲线最小值代表南海沉积物的模型理论速度（1.84 km/s），最大值代表纯水合物的速度（3.08 km/s），纵波速度随着水合物体积分数增大而增大。
![]()
图 5 横向各向同性理论计算的含裂隙充填型水合物的密度和纵波速度Figure 5. The density and P-wave velocity of fracture-filling hydrate calculated by layered media model2. 孔隙充填型、裂隙充填型水合物声学实验模拟
2.1 孔隙充填型水合物声学实验模拟
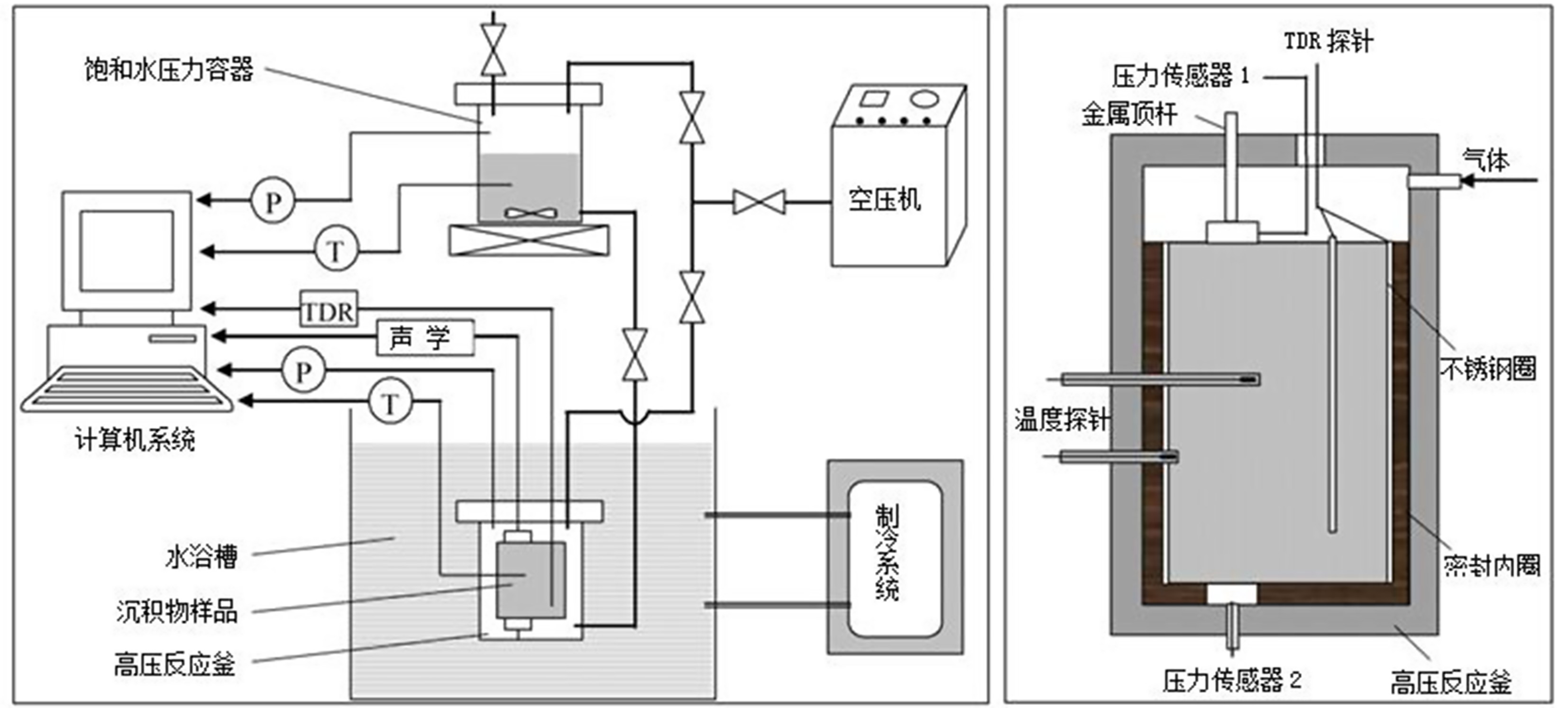
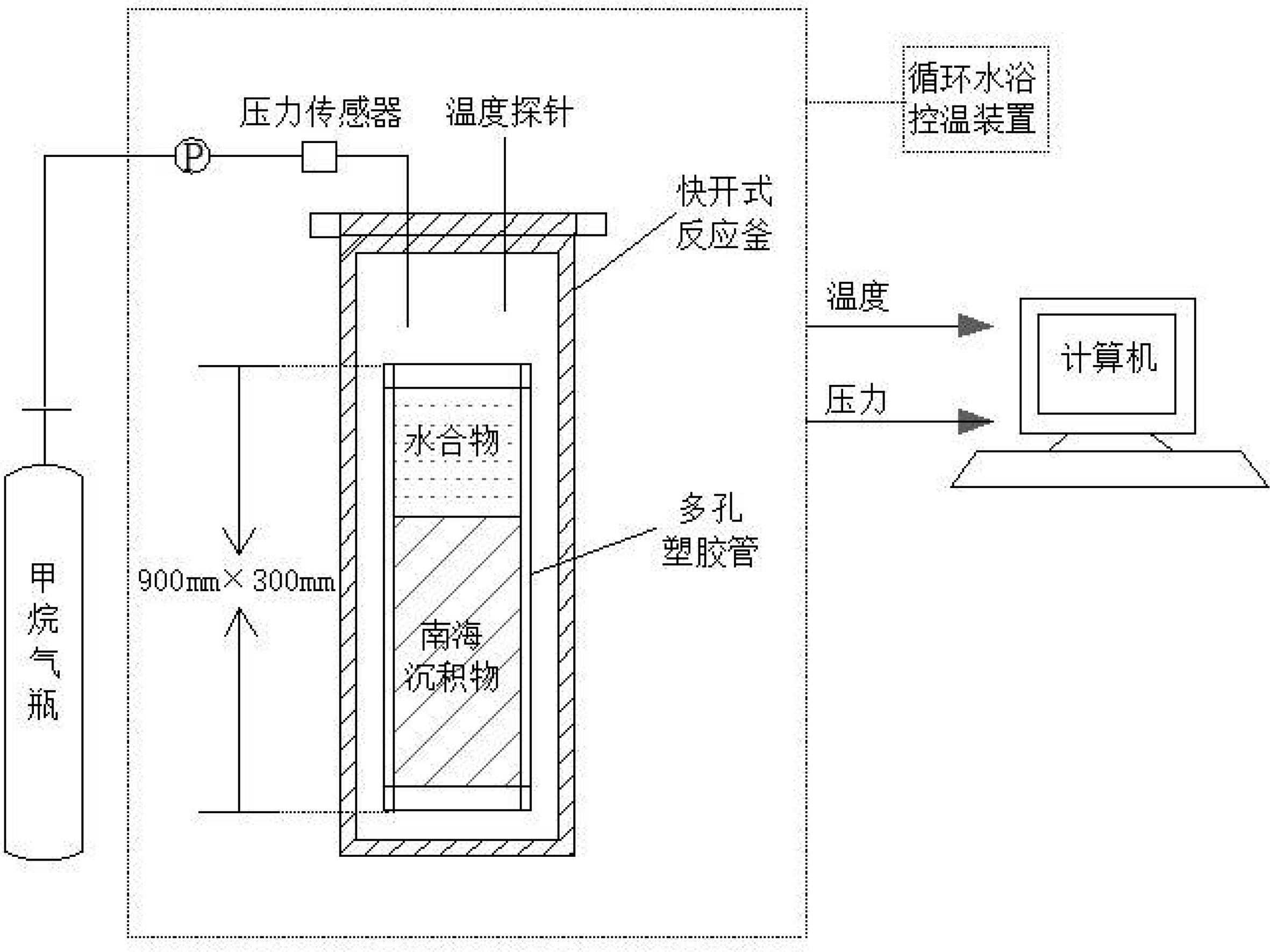
孔隙充填型水合物声学特性模拟实验装置如图6。实验之前需要先对弯曲元超声测速探头的固有声波走时和时域反射技术（TDR）测定沉积物中含水量的误差进行标定。速度测试时需要减去超声探头的固有声波走时，标定结果为
$y = 2.242x \times $ $ {10^{ - 3}} - 0.01246$ 和$y = 9.291x \times {10^{ - 4}} - 9.812 \times {10^{ - 3}}$ ，弯曲元换能器中纵波的固有传播时间为5.56 μs，横波固有传播时间为10.56 μs；TDR实测值与理论值间的误差范围为0.17%～6.75%，由于TDR测量的结果为一个场平均值，因此，TDR系统测试精度满足实验要求。实验模拟过程为：将饱和度水南海沉积物装入高压反应釜，并加入SDS（十二烷基硫酸钠）溶液（加快水合物的生成），通入纯甲烷气体（纯度99.99%）使釜内压力达到目标压力（约7 MPa），并放置24 h使甲烷气溶解到SDS溶液中，随后开启制冷系统使反应釜内部温度到约1 ℃。随着水合物生成，由TDR系统测试水合物的饱和度，弯曲元声波系统测试波速。
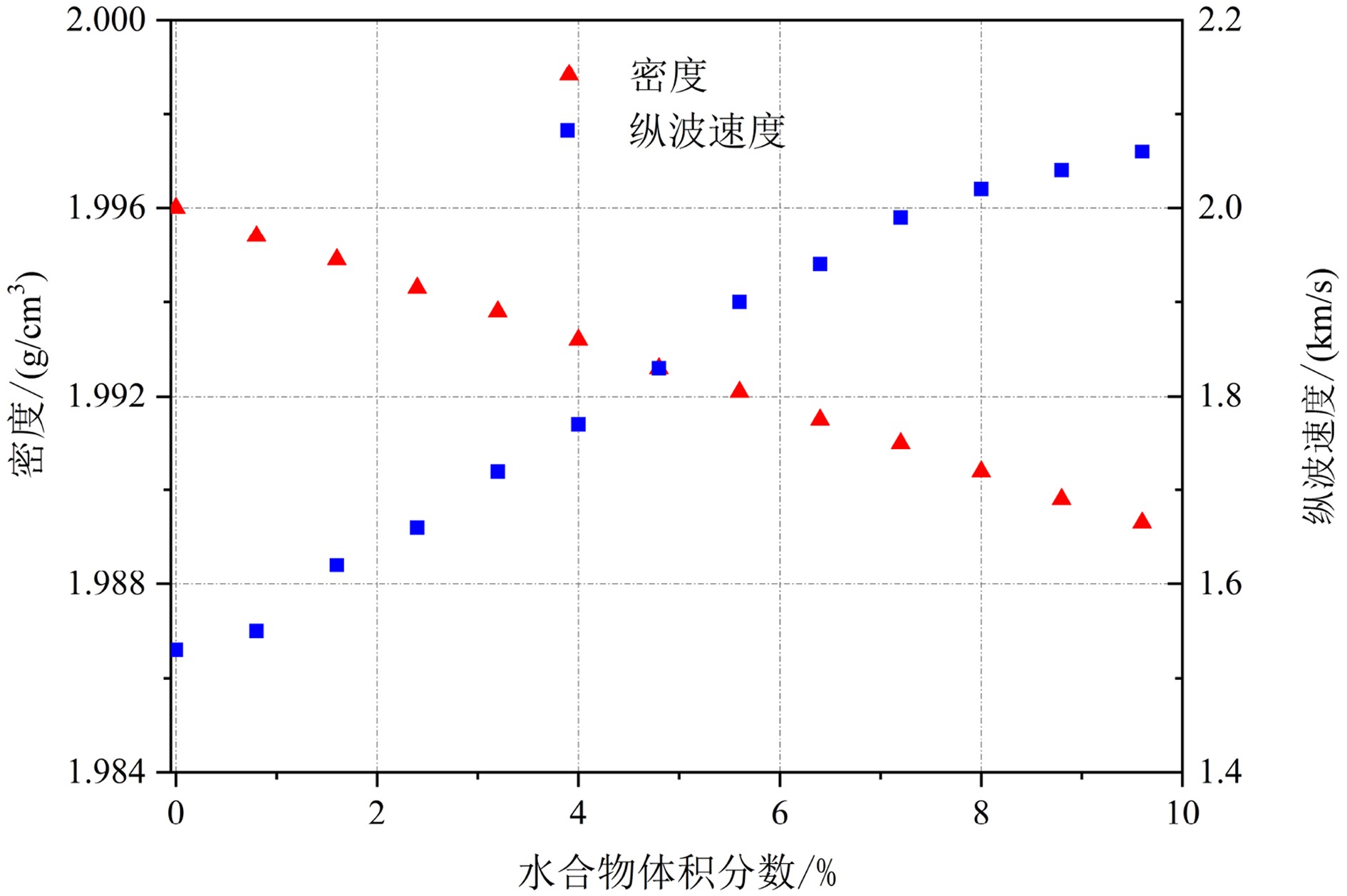
实验中，孔隙充填型水合物的密度由沉积物中矿物及生成的水合物的密度及其含量计算得来。纵波速度为实验测试结果（图7）。由于南海沉积物中短期很难生成高饱和度水合物，因此，反应釜中生成水合物的最大体积分数为9.6%（对应饱和度为24%）。基于实验波速数据发现，纵波速度随水合物体积分数呈正比趋势，当水合物体积分数为9.6%时，沉积介质纵波速度达到最大值2.06 km/s。
![]()
图 7 南海沉积物中孔隙充填型水合物的纵波速度和密度Figure 7. P-wave velocity and density of pore-filling hydrate in deposits of the South China Sea2.2 裂隙充填型水合物声学实验模拟
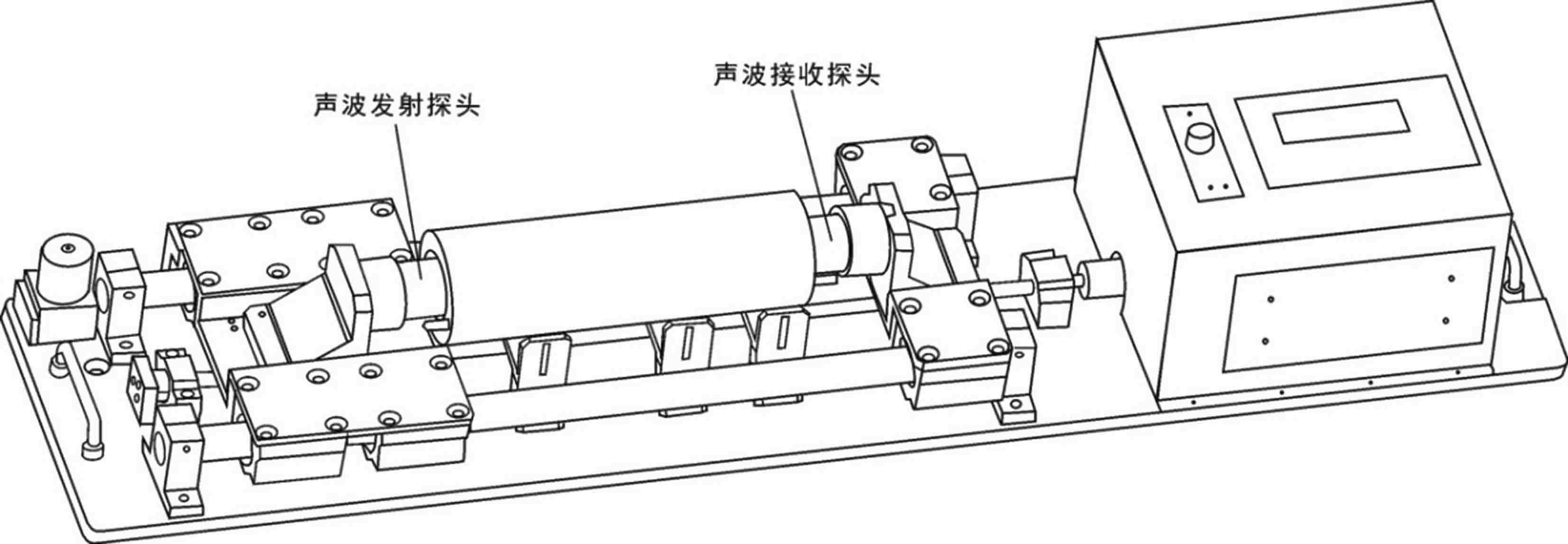
先利用实验装置（图8）进行裂隙充填型水合物实验合成，其过程为：利用雾化喷头将纯水雾化后喷洒到液氮中，合成所需量的冰粉，将冰粉与沉积物按照比例装入多孔塑胶管中，反应釜密封后通入甲烷气使釜内压力达到水合物合成所需目标压力，再将反应釜置于循环水域控温装置中进行降温（约1 ℃），直至水合物合成完毕。最后开釜取出样品，连同塑胶管一同置于岩心夹持器（图9）上，利用超声探头发射/接收声波，进行波速测试。
![]()
图 8 裂隙充填型水合物合成实验装置Figure 8. Experimental apparatus for fracture-filling hydrate synthesis不加入水合物催化溶液时，南海沉积物中短期很难生成孔隙充填型水合物，且长时间内合成的水合物饱和度也很低[21]。该次裂隙充填型水合物合成实验中未向沉积物中加入SDS溶液，一个实验周期（约7天）内沉积物孔隙中几乎不会有水合物生成，实验介质可视为纯裂隙充填型水合物。
含裂隙充填型水合物（裂隙为水平裂隙）的南海沉积介质的密度与纵波速度结果中（图10），密度计算公式为
$\rho = {\eta _1}{\rho _{\rm{h}}} + {\eta _2}\left[ {{\rho _{\rm{s}}}(1 - \phi ) + {\rho _{\rm{w}}}\phi } \right]$ ，其中，${{\rm{\eta }}_{\rm{1}}}$ 和${{\rm{\eta }}_{\rm{2}}}$ 分别为裂隙和沉积物的体积分数，${\rho _{\rm{h}}}$ 为纯水合物的密度，计算取值为0.93 g/cm3，${\rho _{\rm{s}}}$ 为南海泥质黏土沉积物的骨架密度（2.66 g/cm3），${\rm{\phi }}$ 为沉积物孔隙度，${\rho _{\rm{w}}}$ 为水的密度（1 g/cm3）；纵波速度为实验超声测试结果。当水合物体积分数为0时，整个沉积介质的密度即为沉积物的骨架密度（2.66 g/cm3），随着水合物体积分数增大，整个沉积介质（水合物+沉积物）的密度呈减小趋势，而当水合物体积分数为100%时，介质的密度即为纯水合物的密度值（0.93 g/cm3）。水合物体积分数为0和100%分别对应100%南海沉积物和100%纯水合物的波速，当水合物体积分数增大时，纵波速度也随之增大。![]()
图 10 含裂隙充填型水合物的南海沉积介质的密度与纵波速度Figure 10. Density and P-wave velocity of sediment medium of South China Sea with fracture-filling hydrate3. 孔隙充填型、裂隙充填型水合物识别方法
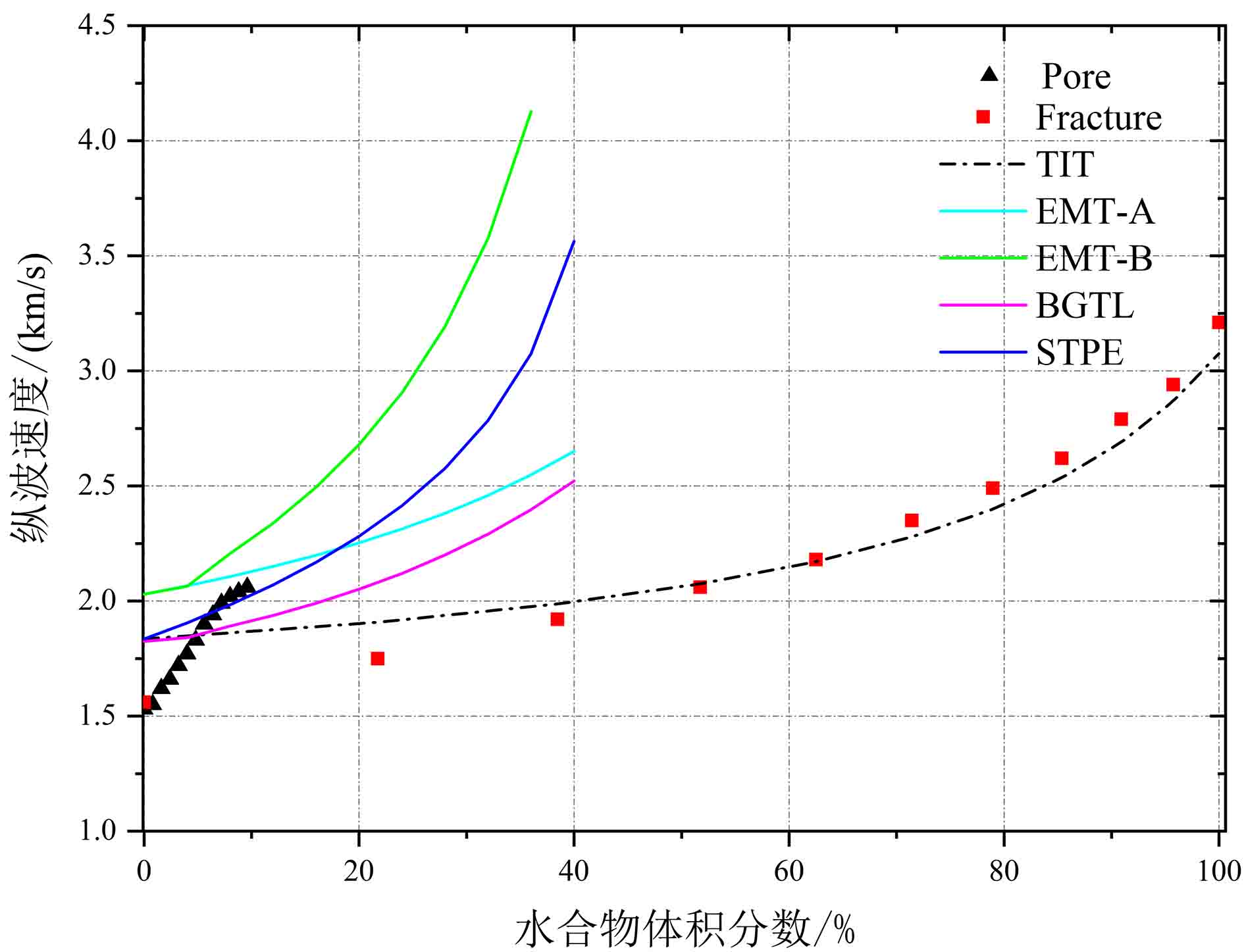
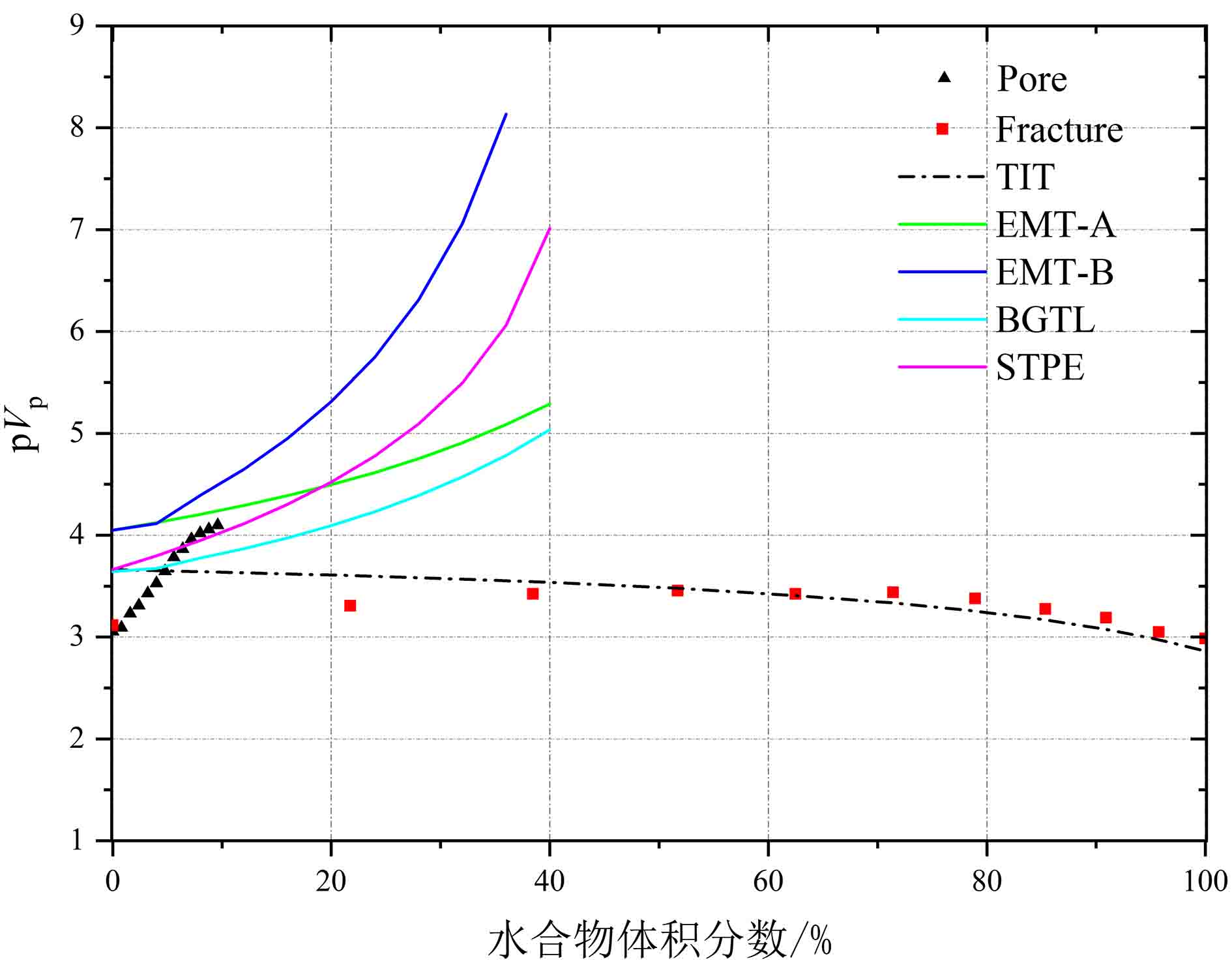
两种类型水合物的岩石物理模拟和实验纵波速度结果中（图11），波速均随水合物体积分数增大而增大。实验中生成的孔隙充填型水合物的最大体积分数为9.6%（对应饱和度为24%）。孔隙充填型水合物的纵波速度在体积分数小于4%（对应饱和度为10%）时低于岩石物理模拟的波速，推断造成该现象的主要原因是当南海沉积物孔隙空间生成的水合物饱和度较低时，水合物呈悬浮状分散于沉积物孔隙内，导致声波信号发生衰减，且这种悬浮状态对沉积物骨架支撑几乎不起作用，故当水合物体积分数（饱和度）较低时，实验模拟的波速低于岩石物理模拟值。而当体积分数大于4%时，实验波速趋向于BGTL模型计算的理论波速。横向各向同性理论（TIT）计算的裂隙充填型（水平裂隙）水合物理论波速在水合物体积分数较大时（＞40%）与实验测试的纵波速度吻合较好，但当水合物体积分数较小时，两者间的最大差为0.27 km/s，整体吻合较好。
![]()
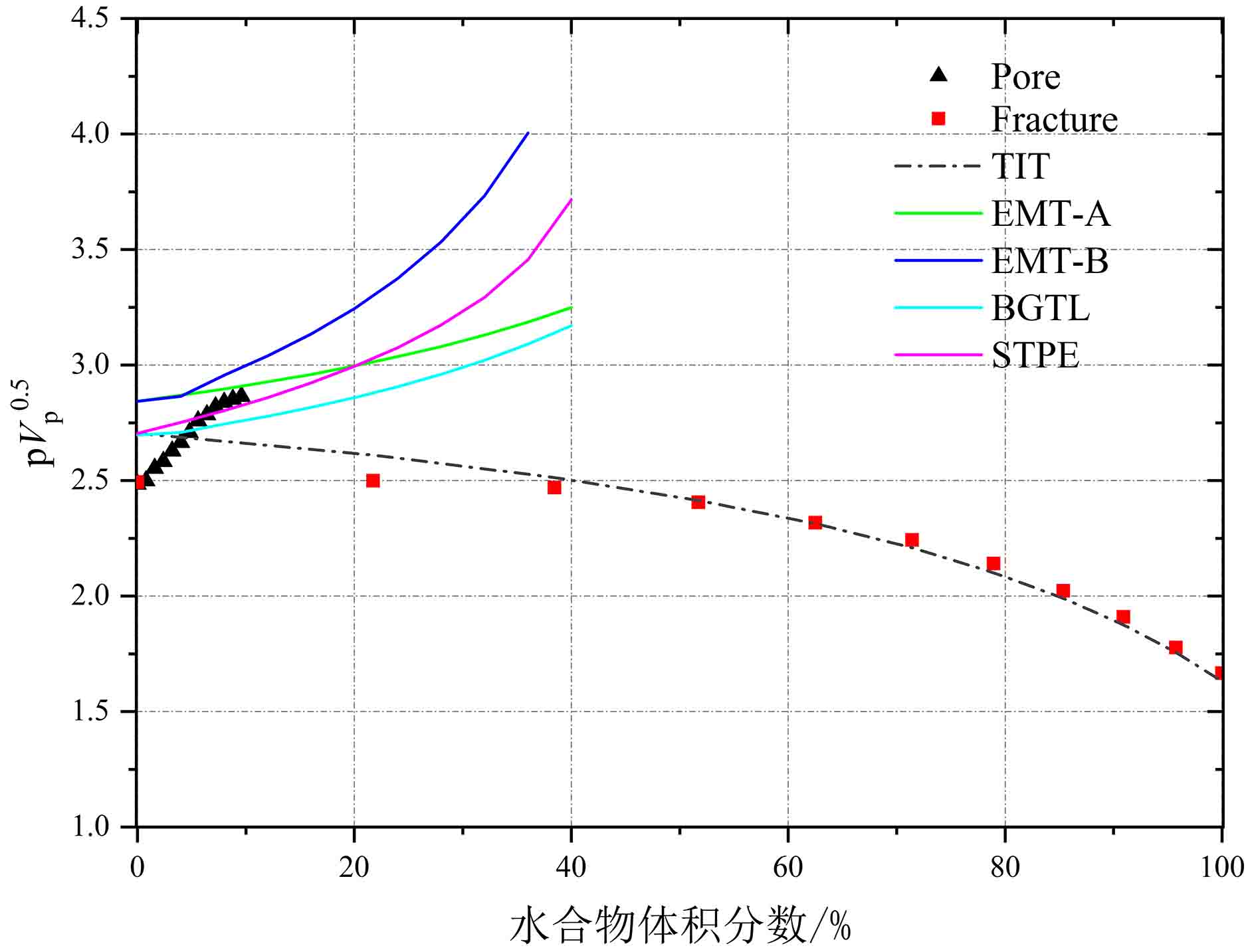
图 11 岩石物理模拟和实验测试的纵波速度Figure 11. The P- wave velocity of petrophysical simulation and experimental test通过将密度与速度参数结合，计算了两种类型水合物的阻抗（ρVp）（图12）和
$\rho {\sqrt V _{\rm{p}}}$ 属性（图13）。由于裂隙填充型水合物的实验阻抗斜率非严格负值，因此，基于阻抗无法进行两种类型水合物的判别。岩石物理模拟和实验测试的$\rho {\sqrt V _{\rm{p}}}$ 属性中，孔隙充填型水合物和裂隙充填型水合物曲线的斜率符号相反：孔隙充填型水合物的$\rho {\sqrt V _{\rm{p}}}$ 属性曲线斜率为正，而裂隙充填型水合物为负。孔隙充填型和裂隙充填型水合物的这一特征为两种类型水合物的判别提供了有效手段。![]()
图 12 岩石物理模拟和实验测试的孔隙充填型和裂隙充填型水合物的阻抗Figure 12. The impedance of pore-filling and fracture-filling hydrates obtained by petrophysical simulation and experimental test![]()
图 13 岩石物理模拟和实验测试的孔隙充填型和裂隙充填型水合物的$\rho {\sqrt V _{\rm{p}}}$ 属性Figure 13. The$\rho {\sqrt V _{\rm{p}}}$ properties of pore-filling and fracture-filling hydrates obtained by petrophysical simulation and experimental test4. 识别方法野外验证
中国第二次天然气水合物钻探航次（GMGS2）在中国南海珠江口盆地东部第16井中同时发现了孔隙充填和裂隙充填型水合物，利用该井的密度和测井资料对
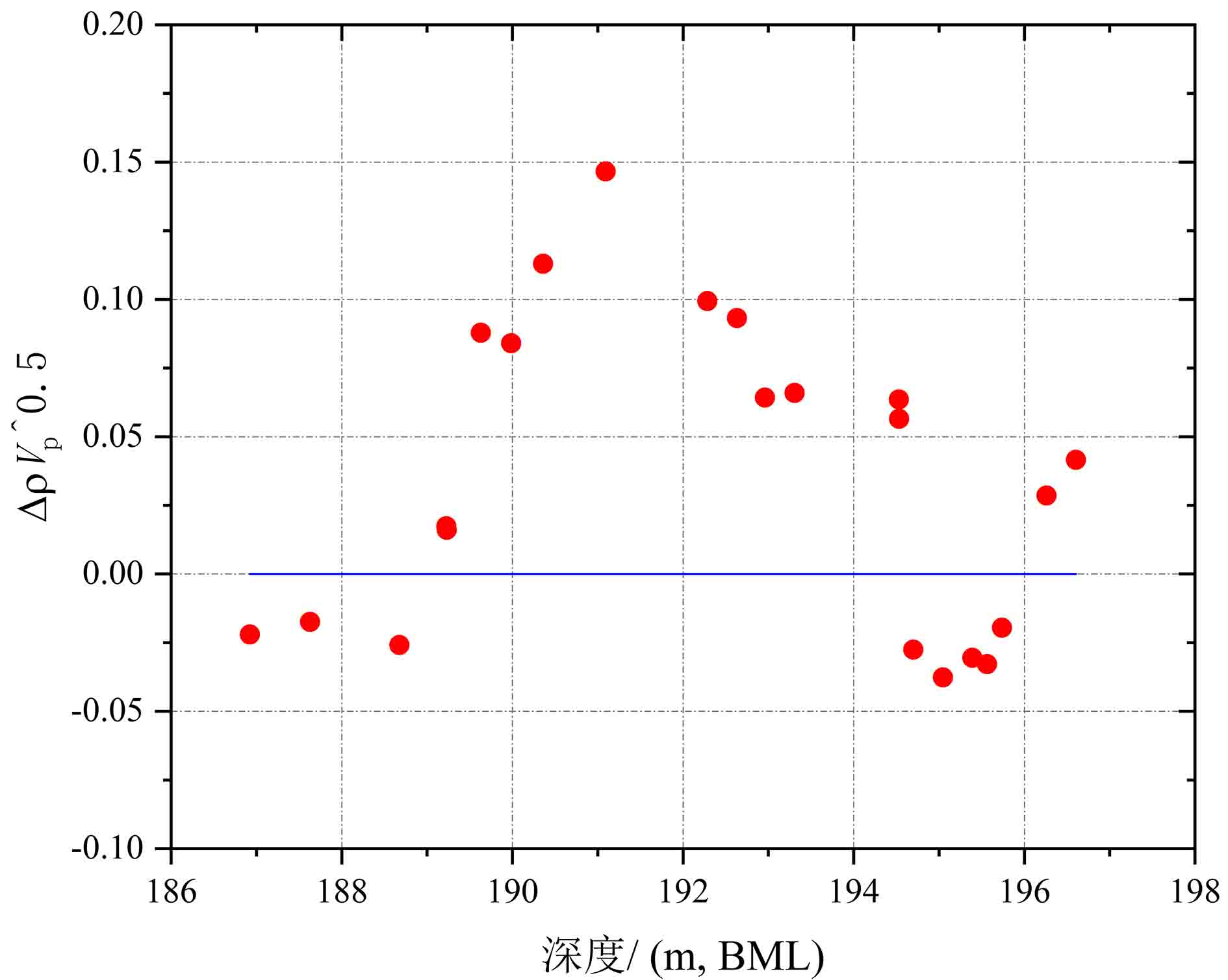
$\rho {\sqrt V _{\rm{p}}}$ 属性识别水合物类型的方法进行验证。该16井中孔隙充填和裂隙充填型水合物平均饱和度分别为42%和50%，其中孔隙充填和裂隙充填型水合物分别位于井深（泥线以下：BML）189～198和10～20 m[18, 24]。该井上部10～20 m验证结果（图14）表明该范围水合物类型以裂隙充填型水合物为主，夹杂部分孔隙充填型水合物。井深10～11.6、14～18.5 m深度含水合物层与背景层的
$\rho {\sqrt V _{\rm{p}}}$ 属性差值小于零，指示该范围内存在裂隙充填型水合物，12～13.6、18.5～20 m深度$\rho {\sqrt V _{\rm{p}}}$ 属性差值大于零，代表赋存的水合物类型为孔隙充填型。井底部189～198 m赋存的水合物类型以孔隙充填型为主（图15），在194～196 m深度夹杂少量裂隙充填型水合物。从验证结果来看，基本与野外观测结果一致。![]()
图 14 GMGS2-16井上部含裂隙充填型水合物储层$\rho {\sqrt V _{\rm{p}}}$ 属性差值结果Figure 14. Result of$\rho {\sqrt V _{\rm{p}}}$ attribute difference of fracture-filling hydrate reservoir in the upper part range of MGMS2-16 Well![]()
图 15 GMGS2-16井下部含孔隙充填型水合物储层$\rho {\sqrt V _{\rm{p}}}$ 属性差值结果Figure 15. Result of$\rho {\sqrt V _{\rm{p}}}$ attribute difference of pore-filling hydrate reservoir in the lower part of GMGS2-16 Well5. 结论与展望
密度和纵波速度间的差异提供了识别孔隙充填型水合物和裂隙充填型水合物在沉积物中赋存形态的基础。通过结合岩石物理模型和实验模拟，获得了南海沉积物中孔隙充填型和裂隙充填型水合物的密度和纵波速度参数，测试了两种类型水合物的阻抗和
$\rho {\sqrt V _{\rm{p}}}$ 属性。研究结果表明基于$\rho {\sqrt V _{\rm{p}}}$ 属性可以有效识别孔隙型充填和裂隙充填型水合物：对于含孔隙充填型水合物的南海沉积物，岩石物理模型的$\rho {\sqrt V _{\rm{p}}}$ 属性与实验测试的$\rho {\sqrt V _{\rm{p}}}$ 属性曲线都是正斜率；对于含裂隙充填型水合物的南海沉积物，岩石物理模型和实验测试的$\rho {\sqrt V _{\rm{p}}}$ 属性都为负斜率。对于含孔隙充填型水合物的南海沉积介质，当水合物体积分数大于4%时，岩石物理模型计算的$\rho {\sqrt V _{\rm{p}}}$ 属性与实验数据吻合较好，尤其是STPE模型与实验结果吻合最佳，因此，STPE模型在计算南海沉积物中水合物的饱和度时相比其他模型更具优势。对于裂隙充填型水合物，当水合物体积分数较低（＜40%）时，横向各向同性理论计算的$\rho {\sqrt V _{\rm{p}}}$ 属性和实验测试结果存在明显差异。因此，当水合物体积分数低于40%时，计算水合物的$\rho {\sqrt V _{\rm{p}}}$ 属性过程中需要对模型进行适当修正。最后利用
$\rho {\sqrt V _{\rm{p}}}$ 属性对GMGS2航次16井赋存的孔隙充填和裂隙充填型水合物进行了验证表明结果与实际钻探结果一致，因此，利用$\rho {\sqrt V _{\rm{p}}}$ 属性识别孔隙充填和裂隙充填型水合物具有理论和实际可行性。附录（岩石物理模型）
A.1 等效介质理论（EMT）
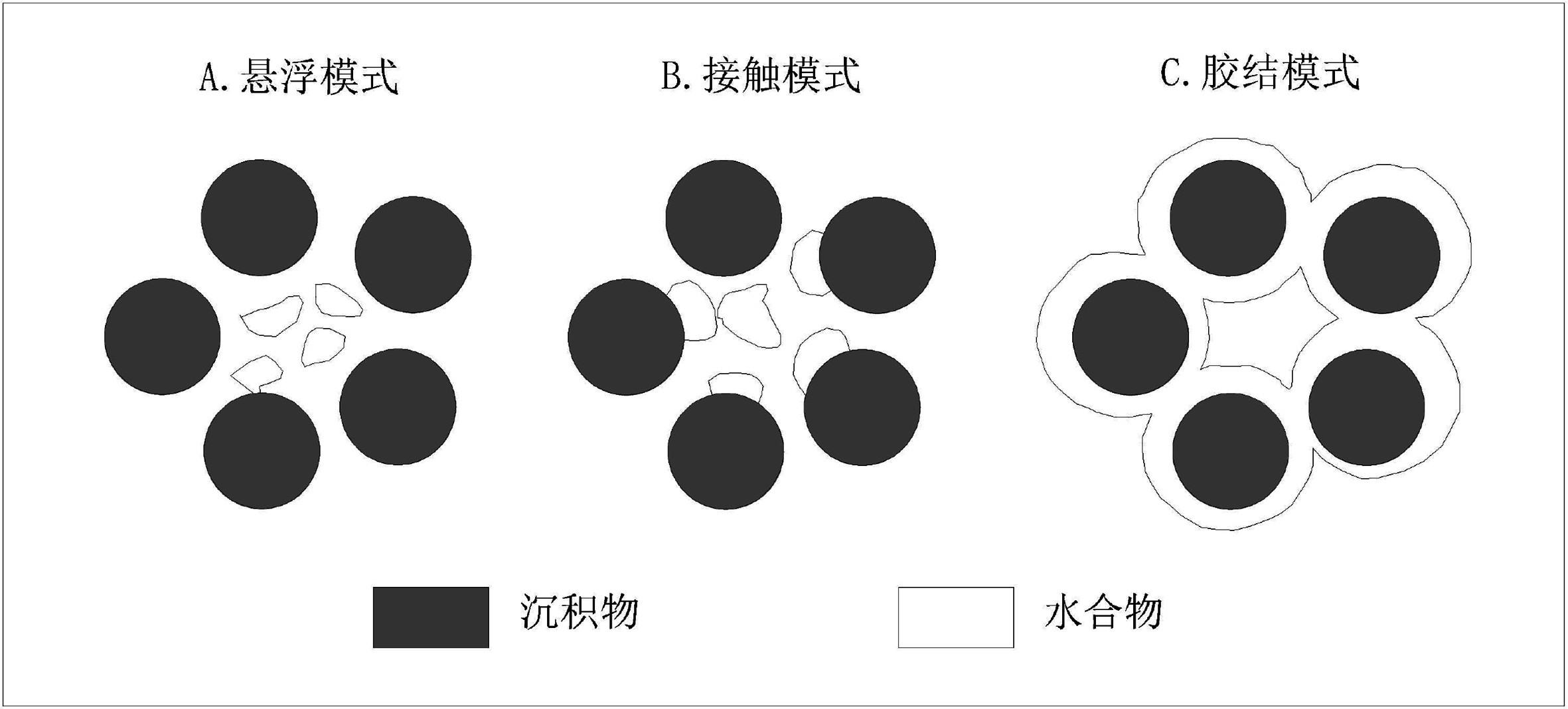
Helgerud等[25-26]对水合物微观分布形态进行了研究，认为水合物与沉积物颗粒间的共生关系主要是充填于沉积物孔隙中，或胶结了沉积物骨架，与骨架呈支撑形态（图A-1）。对于模式A，水合物的生成替代了沉积物孔隙中的流体并占据了流体空间，因而该模式中，水合物也被认为是孔隙流体的一部分；模式B中，水合物被当作沉积物骨架的一部分，孔隙空间中只有流体，该模式对沉积物骨架的密度、体积模量和剪切模量产生了影响[21]；模式C中，孔隙度的降低等同于模式B，另一方面，岩石骨架的体积模量和剪切模量发生了改变。南海沉积物中孔隙充填型水合物模拟选用A（水合物充当流体部分）和B（水合物充当骨架部分）模式进行计算。
（1）模式A
沉积介质的纵波速度及密度计算公式如下：
$$\tag{A-1}\begin{array}{l} {V_{\rm{p}}} = \sqrt {\frac{{{K_{{\rm{sat}}}} + \displaystyle\frac{4}{3}{G_{{\rm{sat}}}}}}{{{\rho _{\rm{b}}}}}} \\ {\rho _{\rm{b}}} = (1 - \phi ){\rho _{\rm{s}}} + \phi {\rho _{\rm{f}}} \end{array}$$ 式中，Ksat和Gsat分别是等效介质的体积模量和剪切模量；
${\rho _{\rm{s}}}$ 和${\rho _{\rm{f}}}$ 分别为岩石固相和流体相的体积密度。ϕc为临界孔隙度，一般取0.36～0.40 [27]。当沉积物中充填体积模量为Kf的流体时，可以根据Gassmann方程，通过如下公式得到沉积物的体积模量Ksat和剪切模量Gsat：$$\tag{A-2}{K_{\rm{sat}}} = {K_{\rm{ma}}}\frac{{\phi {K_{\rm{dry}}} - (1 + \phi ){K_{\rm f}}{K_{\rm{dry}}}/{K_{\rm{ma}}} + {K_{\rm f}}}}{{(1 - \phi ){K_{\rm f}} + \phi {K_{\rm{ma}}} - {K_{\rm f}}{K_{\rm{dry}}}/{K_{\rm{ma}}}}}$$ $$\tag{A-3}{G_{{\rm{sat}}}} = {G_{{\rm{dry}}}}$$ 式中，Kma为岩石固相的体积模量，Kdry和Gdry分别为干岩石的体积模量和剪切模量，Kf为流体的体积模量。模式A中，孔隙中有水合物生成，因此，Kf计算公式为：
$$\tag{A-4}{K_{\rm f}} = {\left[\frac{{1 - {S_{\rm h}}}}{{{K_{\rm w}}}} + \frac{{{S_{\rm h}}}}{{{K_{\rm h}}}}\right]^{ - 1}}$$ 式中，Sh、Kh分别代表水合物占孔隙的体积分数和水合物的体积模量，Kw为水的体积模量。
式（A-2）中，Kdry和Gdry的计算公式为：
$$\tag{A-5}{K_{\rm{dry}}} \!= \left\{ {\begin{array}{*{20}{c}} {{{\left[\frac{{\phi /{\phi _{\rm c}}}}{{{K_{\rm{HM}}} + \displaystyle\frac{4}{3}{G_{\rm{HM}}}}} + \frac{{1 - \phi /{\phi _{\rm c}}}}{{{K_{\rm{ma}}} + \displaystyle\frac{4}{3}{G_{\rm{HM}}}}}\right]}^{ - 1}} \!-\! \displaystyle\frac{4}{3}{G_{\rm{HM}}},\phi < {\phi _{\rm c}}} \\ {{{\left[\frac{{(1 - \phi )/(1 - {\phi _{\rm c}})}}{{{K_{\rm{HM}}} + \displaystyle\frac{4}{3}{G_{\rm{HM}}}}} + \frac{{(\phi - {\phi _{\rm c}})/(1 - {\phi _{\rm c}})}}{{\displaystyle\frac{4}{3}{G_{\rm{HM}}}}}\right]}^{ - 1}} \!-\! \displaystyle\frac{4}{3}{G_{\rm{HM}}},\phi \geqslant {\phi _{\rm c}}} \end{array}} \right.$$ $$\tag{A-6}{G_{\rm{dry}}} \!= \left\{ {\begin{array}{*{20}{l}} {{{\left[\displaystyle\frac{{\phi /{\phi _{\rm c}}}}{{{G_{\rm{HM}}} + Z}} \!+\! \frac{{1 - \phi /{\phi _{\rm c}}}}{{G + Z}}\right]}^{ - 1}} - Z,\phi < {\phi _{\rm c}}} \\ {{{\left[\displaystyle\frac{{(1 \!-\! \phi )/(1 - {\phi _{\rm c}})}}{{{G_{\rm{HM}}} + Z}} \!+\! \frac{{(\phi \!-\! {\phi _{\rm c}})/(1 \!-\! {\phi _{\rm c}})}}{Z}\right]}^{ - 1}} \!- \!Z,\phi \geqslant {\phi _{\rm c}}} \end{array}} \right.$$ $$\tag{A-7}Z = \frac{{{G_{\rm{HM}}}}}{6}\left(\frac{{9{K_{\rm{HM}}} + 8{G_{\rm{HM}}}}}{{{K_{\rm{HM}}} + 2{G_{\rm{HM}}}}}\right).$$ 其中，
$$\tag{A-8}\begin{split} {K_{\rm{HM}}} =& {\left[\displaystyle\frac{{{n^2}{{(1 - {\phi _{\rm c}})}^2}{G_{\rm{ma}}}^2}}{{18{\pi ^2}{{(1 - \nu )}^2}}}P\right]^{\frac{1}{3}}}\\ {G_{\rm{HM}}} =&\displaystyle\frac{{5 - 4\nu }}{{5(2 - \nu )}}{\left[\frac{{3{n^2}{{(1 - {\phi _{\rm c}})}^2}{G_{\rm{ma}}}^2}}{{2{\pi ^2}{{(1 - \nu )}^2}}}P\right]^{\frac{1}{3}}} \end{split} $$ 式（A-8）中，P为有效压力；Kma、Gma分别是岩石骨架的体积模量、剪切模量，由公式（A-13）计算；ν是岩石骨架的泊松比，且
$\nu = 0.5({K_{\rm{ma}}} - \displaystyle\frac{2}{3}{G_{\rm{ma}}})/({K_{\rm{ma}}} +$ $ {G_{\rm{ma}}}/3) $ ；n为临界孔隙度时单位体积内颗粒平均接触的数目，一般取8～9.5[28-29]。（2）模式B
模式B中水合物被认为是岩石骨架的一部分，产生了两个效应：一个是使孔隙度减小，另一个是改变了骨架的体积模量和剪切模量。因此，在模式A的基础上，需对沉积物孔隙度进行修正，即ϕr=ϕ(1-Sh)。同时，应将水合物作为矿物组分代入公式（A-9）来计算岩石的Kma和Gma。此外，沉积物孔隙中只有水，孔隙流体密度和体积模量等直接用水的替代。
A.2 BGTL理论
BGTL理论（Biot-Gassmann Theory modified by Lee的简称）建立在经典的BGT理论（Biot-Gassmann Theory）上，在预测速度时不仅考虑了分压的影响，而且还考虑了岩石的孔隙度、固结度等因素的影响，其公式为：
$$\tag{A-9}{V_{\rm{p}}} = \sqrt {\frac{{k + 4\mu /3}}{\rho }} ,{V_{\rm s}} = \sqrt {\frac{\mu }{\rho }} $$ 式中，
$k$ 、$\mu $ 分别为沉积介质的体积模量和剪切模量。$$\tag{A-10}k = {k_{\rm{ma}}}(1 - \beta ) + {\beta ^2}M,\frac{1}{M} = \frac{{\beta - \phi }}{{{k_{\rm{ma}}}}} + \frac{\phi }{{{k_{\rm{fl}}}}}$$ 式中，
${k_{\rm{ma}}}$ 为岩石骨架的体积模量，${k_{\rm{fl}}}$ 为孔隙中流体的体积模量；$\beta $ 是Biot系数，表征了流体体积变化与岩石体积变化的比值，与沉积介质的孔隙度有关；M为一模量，表征了沉积介质体积不变的情况下，将一定量的水压入沉积介质所需要的静水压力增量[30]。BGTL理论假设沉积介质速度比率与沉积物基质速度比率之间存在如下关系：$$\tag{A-11}{V_s} = {V_{\rm{p}}}G\alpha {(1 - \phi )^n}$$ 式中，
$\alpha $ 为基质部分的Vs/Vp，G是与沉积物中黏土含量有关的常数，n取决于分压大小及岩石的固结程度。由公式（B-2）和（B-3）得出沉积介质的剪切模量为：
$$\tag{A-12}\mu = \frac{{{\mu _{\rm{ma}}}{G^2}{{(1 - \phi )}^{2n}}k}}{{{k_{\rm{ma}}} + 4{\mu _{\rm{ma}}}[1 - {G^2}{{(1 - \phi )}^{2n}}]/3}}$$ 式中，
${\mu _{\rm{ma}}}$ 为岩石骨架的剪切模量。${k_{\rm{ma}}}$ 和${\mu _{\rm{ma}}}$ 由Hill平均方程计算[31]:$$\tag{A-13}\begin{array}{l}{k_{\rm{ma}}} = \displaystyle\frac{1}{2}\left[\sum\limits_{i = 1}^m {{f_i}} {k_i} + {\left(\sum\limits_{i = 1}^m {{f_i}/{k_i}} \right)^{ - 1}}\right],\\ {\mu _{\rm{ma}}} = \displaystyle\frac{1}{2}\left[\sum\limits_{i = 1}^m {{f_i}{\mu _i} + {{\left(\sum\limits_{i = 1}^m {{f_i}/{\mu _i}} \right)}^{ - 1}}} \right] \end{array}$$ 式中，m为岩石固相部分中矿物的种数，
${f_i}$ 为第i种矿物占固相部分的体积分数；${k_i}$ 和${\mu _i}$ 分别为第i种矿物的体积模量和剪切模量。A.3 简化三相方程（STPE）
利用Lee[32]的简化三相方程（STPE）可以计算各向同性的气体水合物填充沉积物孔隙空间的速度。Lee推导出低频下气体水合物填充沉积物孔隙空间的体积模量和剪切模量，用于测井和地震数据:
$$\tag{A-14}k = {K_{\rm{ma}}}\left( {1 - {{\rm{\beta }}_{\rm{p}}}} \right){\rm{ + }}{{\rm{\beta }}_{\rm{p}}}^{\rm{2}}{K_{{\rm{av}}}},{\rm{\mu }} = {{\rm{\mu }}_{\rm{ma}}}\left( {{\rm{1 - }}{{\rm{\beta }}_{\rm{s}}}} \right)$$ $$\tag{A-15}\frac{1}{{{K_{\rm{av}}}}}{\rm{ = }}\frac{{{{\rm{\beta }}_{\rm{p}}}{\rm{ - }}{\rm{\phi }}}}{{{K_{\rm{ma}}}}} + \frac{{{{\rm{\phi }}_{\rm w}}}}{{{k_{\rm w}}}} + \frac{{{{\rm{\phi }}_{\rm h}}}}{{{K_{\rm h}}}},{{\rm{\beta }}_{\rm p}} = \frac{{{{\rm{\phi }}_{\rm{as}}}\left( {1 + {\rm{\alpha }}} \right)}}{{1 + {\rm{\alpha }}{{\rm{\phi }}_{\rm{as}}}}},{{\rm{\beta }}_{\rm s}} = \frac{{{{\rm{\phi }}_{\rm {as}}}\left( {1 + {\rm{\gamma \alpha }}} \right)}}{{1 + {\rm{\gamma \alpha }}{{\rm{\phi }}_{\rm {as}}}}}$$ $$\tag{A-16}{{\rm{\phi }}_{{\rm{as}}}} = {{\rm{\phi }}_{\rm w}} + {\rm{\varepsilon }}{{\rm{\phi }}_{\rm h}},{{\rm{\phi }}_{\rm w}} = (1 - {S_{\rm h}}){\rm{\phi }},{\rm{\phi }}h = {S_{\rm h}}{\rm{\phi }}$$ 式中，α为固结参数，γ是与剪切模量相关参数，可由公式γ=(1+2α)/(1+α)得到，Kma，Kw和Kh是骨架、水和水合物的体积模量，μma是骨架的剪切模量，ϕ为孔隙度。参数ε是水合物形成使沉积物骨架发生硬化的降低量，Lee推荐使用ε=0.12为建模数值。气体水合物填充沉积物孔隙空间的纵横波速度可由下式得：
$$\tag{A-17}{V_{\rm{p}}} = \sqrt {\frac{{k + 4\mu /3}}{\rho }} ,{V_{\rm{s}}} = \sqrt {\frac{\mu }{\rho }} $$ $$\tag{A-18}{\rho _{\rm{b}}} = {\rho _{\rm{s}}}\left( {1 - {\rm{\phi }}} \right) + {\rho _{\rm{w}}}{\rm{\phi }}\left( {1 - {S_{\rm{h}}}} \right){\rm{ + }}{\rho _{\rm{h}}}{\rm{\phi }}{S_{\rm{h}}}$$ 式中，
$\rho $ 是水合物填充沉积物孔隙空间的体积密度，固结参数α取决于沉积物的有效压力和固结程度。Mindlin[33]表明体积模量和剪切模量取决于有效压力的1/3次方。基于Mindlin的这一理论，深度或有效压力相关的α可由下式得：$$\tag{A-19}{{\rm{\alpha }}_{\rm{i}}} = {{\rm{\alpha }}_0}{({P_0}/{P_i})^n} \approx {{\rm{\alpha }}_0}{({d_0}/{d_i})^n}$$ 式中，α0是有效压力P0或深度d0处的固结参数，αi是有效压力Pi或深度di处的固结参数。
B.1 横向各向同性理论模型
层状介质的两端元模型（图7）表示为：
$$\tag{B-1}\left\langle G \right\rangle = {\eta _1}{G_1} + {\eta _2}{G_2},{\left\langle {\frac{1}{G}} \right\rangle ^{ - 1}} = {\left( {\frac{{{\eta _1}}}{{{G_1}}} + \frac{{{\eta _2}}}{{{G_2}}}} \right)^{ - 1}}$$ 式中，
${G_1}$ 、${G_{\rm{2}}}$ 分别代表模型中组分1和组分2的任意弹性参数或参数组合，${\eta _1}$ 和${\eta _{\rm{2}}}$ 分别代表组分1和组分2的体积分数。模型相速度可以根据White由拉梅常数[34]求得：$$\tag{B-2}{V_p} = {\left( {\frac{{A{{\sin }^2}\varphi + C{{\cos }^2}\varphi + L + Q}}{{2\rho }}} \right)^{1/2}}$$ $$\tag{B-3}{V_s}^H = {\left( {\frac{{N{{\sin }^2}\varphi + L{{\cos }^2}\varphi }}{\rho }} \right)^{1/2}}$$ 其中：
$$\tag{B-4}A = \left\langle {\frac{{4\mu (\lambda + \mu )}}{{(\lambda + 2\mu )}}} \right\rangle + {\left\langle {\frac{1}{{(\lambda + 2\mu )}}} \right\rangle ^{ - 1}}{\left\langle {\frac{\lambda }{{(\lambda + 2\mu )}}} \right\rangle ^2}$$ $$\tag{B-5}C = {\left\langle {\frac{1}{{(\lambda + 2\mu )}}} \right\rangle ^{ - 1}}$$ $$\tag{B-6}F = {\left\langle {\frac{1}{{(\lambda + 2\mu )}}} \right\rangle ^{ - 1}}\left\langle {\frac{\lambda }{{(\lambda + 2\mu )}}} \right\rangle $$ $$\tag{B-7}L = {\left\langle {\frac{1}{\mu }} \right\rangle ^{ - 1}}$$ $$\tag{B-8}N = \left\langle \mu \right\rangle $$ $$\tag{B-9}\rho = \left\langle \rho \right\rangle $$ $$\tag{B-10}Q \!=\! \sqrt {{{[(A \!-\! L){{\sin }^2}\varphi \!-\! (C \!-\! L){{\cos }^2}\varphi ]}^2} \!+\! 4{{(F \!+\! L)}^2}{{\sin }^2}\varphi {{\cos }^2}\varphi } $$ 其中，Vp和VsH分别代表纵波速度和水平极化横波速度，参数
$ \varphi $ 代表入射波传播方向相对于裂隙对称轴的夹角。根据Thomson[35]，群速度与相速度间的关系可表述为：
$$\tag{B-11}{V_{\rm{p}}}\left( {\rm{\varphi }} \right){\rm{ = }}G{V_{\rm{p}}}\left( {{{\rm{\varphi }}_{\rm{g}}}} \right),{V_{\rm{s}}}^H\left( {\rm{\varphi }} \right) = G{V_{\rm{s}}}^H\left( {{{\rm{\varphi }}_{\rm{g}}}} \right)$$ 式中：GVp和GVsH分别代表Vp和VsH的群速度，
$ {\varphi }_{g} $ 是射线方向和裂隙同相轴间的夹角，可由下式求得：纵波：
$$\tag{B-12}\tan {{\rm{\varphi }}_{\rm{g}}} = {\rm{tan}}{\rm{\varphi }}[1 + 2\delta + {\rm{4}}(\varepsilon - \delta ){\rm{si}}{{\rm{n}}^2}{\rm{\varphi }}]$$ SH波：
$$\tag{B-13}\tan {{\rm{\varphi }}_{\rm g}} = \tan {\rm{\varphi }}(1 + 2\gamma )$$ 其中：
${\rm{\gamma }} = \displaystyle\frac{{N - L}}{{2L}},{\rm{\delta }} = \frac{{{{(F + L)}^2} - {{(C - L)}^2}}}{{2C(C - L)}},{\rm{\varepsilon }} = \frac{{A - C}}{{2C}}$ ，γ，$ \mathrm{\delta } $ 和$ \mathrm{\varepsilon } $ 是表征横向各向同性介质属性的参数。 -
![]()
图 1 裂隙充填型水合物的类型[20]
a. 裂隙空间发育的纯水合物，b. 黏土质沉积物夹杂含水合物的砂质沉积介质， c. 黏土沉积物中发育连续微裂隙中的水合物，d. 黏土沉积物中不连续微裂隙中的水合物。
Figure 1. Types of fracture-filling hydrates[20]
a. Pure hydrate in fracture space， b. sandy sedimentary medium with hydrate in clay sediment，c. hydrate in continuous microfractures developed in clay sediments，d. hydrate in discontinuous microfractures in clay sediments.
![]()
图 2 EMT、BGTL、STPE模型计算的含孔隙充填型水合物的密度
Figure 2. The density of pore-filling hydrate calculated by EMT、BGTL and STPE models
![]()
图 3 EMT、BGTL、STPE模型计算的含孔隙充填型水合物的纵波速度
Figure 3. The P-wave velocity of pore-filling hydrate calculated by EMT、BGTL and STPE models
![]()
![]()
图 5 横向各向同性理论计算的含裂隙充填型水合物的密度和纵波速度
Figure 5. The density and P-wave velocity of fracture-filling hydrate calculated by layered media model
![]()
图 7 南海沉积物中孔隙充填型水合物的纵波速度和密度
Figure 7. P-wave velocity and density of pore-filling hydrate in deposits of the South China Sea
![]()
图 8 裂隙充填型水合物合成实验装置
Figure 8. Experimental apparatus for fracture-filling hydrate synthesis
![]()
图 10 含裂隙充填型水合物的南海沉积介质的密度与纵波速度
Figure 10. Density and P-wave velocity of sediment medium of South China Sea with fracture-filling hydrate
![]()
图 11 岩石物理模拟和实验测试的纵波速度
Figure 11. The P- wave velocity of petrophysical simulation and experimental test
![]()
图 12 岩石物理模拟和实验测试的孔隙充填型和裂隙充填型水合物的阻抗
Figure 12. The impedance of pore-filling and fracture-filling hydrates obtained by petrophysical simulation and experimental test
![]()
图 13 岩石物理模拟和实验测试的孔隙充填型和裂隙充填型水合物的
$\rho {\sqrt V _{\rm{p}}}$ 属性Figure 13. The
$\rho {\sqrt V _{\rm{p}}}$ properties of pore-filling and fracture-filling hydrates obtained by petrophysical simulation and experimental test![]()
图 14 GMGS2-16井上部含裂隙充填型水合物储层
$\rho {\sqrt V _{\rm{p}}}$ 属性差值结果Figure 14. Result of
$\rho {\sqrt V _{\rm{p}}}$ attribute difference of fracture-filling hydrate reservoir in the upper part range of MGMS2-16 Well![]()
图 15 GMGS2-16井下部含孔隙充填型水合物储层
$\rho {\sqrt V _{\rm{p}}}$ 属性差值结果Figure 15. Result of
$\rho {\sqrt V _{\rm{p}}}$ attribute difference of pore-filling hydrate reservoir in the lower part of GMGS2-16 Well -
[1] Ghosh R, Sain K, Ojha M. Effective medium modeling of gas hydrate-filled fractures using the sonic log in the Krishna-Godavari basin, offshore eastern India [J]. Journal of Geophysical Research, 2010, 115(B6): B06101.
[2] Hu G W, Ye Y G, Zhang J, et al. Acoustic response of gas hydrate formation in sediments from South China Sea [J]. Marine and Petroleum Geology, 2014, 52: 1-8. doi: 10.1016/j.marpetgeo.2014.01.007
[3] 王吉亮, 王秀娟, 钱进. 裂隙充填型天然气水合物的各向异性分析及饱和度估算:以印度东海岸NGHP01-10D井为例[J]. 地球物理学报, 2013, 56(4):1312-1320. [WANG Jiliang, WANG Xiujuan, QIAN Jin, et al. Anisotropic analysis and saturation estimation of gas hydrate filled in fractures: a case of site NGHP01-10D, offshore eastern India [J]. Chinese Journal of Geophysics, 2013, 56(4): 1312-1320. doi: 10.6038/cjg20130425 [4] 景鹏飞, 胡高伟, 卜庆涛. 天然气水合物地球物理勘探技术的应用及发展[J]. 地球物理学进展, 2019, 34(5):2046-2064. [JING Pengfei, HU Gaowei, BU Qingtao, et al. Application and development of geophysical technology in gas hydrate exploration [J]. Progress in Geophysics, 2019, 34(5): 2046-2064. doi: 10.6038/pg2019CC0259 [5] 钱进, 王秀娟, 董冬冬, 等. 裂隙充填型天然气水合物的地震各向异性数值模拟[J]. 海洋地质与第四纪地质, 2015, 35(4):149-154. [QIAN Jin, WANG Xiujuan, DONG Dongdong, et al. Seismic anisotropic modeling of fracture-filling gas hydrate [J]. Marine Geology & Quaternary Geology, 2015, 35(4): 149-154. [6] Holland M, Schultheiss P, Roberts J, et al. Observed gas hydrate morphologies in marine sediments[C]//Proceedings of the 6th International Conference on Gas Hydrate. Vancouver, British Columbia, 2008.
[7] Wang X J, Hutchinson D R, Wu S G, et al. Elevated gas hydrate saturation within silt and silty clay sediments in the Shenhu area, South China Sea [J]. Journal of Geophysical Research, 2011, 116(B5): B05102.
[8] Collett T S, Lee M W, Zyrianova M V, et al. Gulf of Mexico gas hydrate joint industry project leg II logging-while-drilling data acquisition and analysis [J]. Marine and Petroleum Geology, 2012, 34(1): 41-61. doi: 10.1016/j.marpetgeo.2011.08.003
[9] Horozal S, Lee G H, Yi B Y, et al. Seismic indicators of gas hydrate and associated gas in the Ulleung Basin, East Sea (Japan Sea) and implications of heat flows derived from depths of the bottom-simulating reflector [J]. Marine Geology, 2009, 258(1-4): 126-138. doi: 10.1016/j.margeo.2008.12.004
[10] Collett T S, Scientific Party N. Occurrence of marine gas hydrates in the Indian continental margin: results of the Indian National Gas Hydrate Program (NGHP) expedition 01[C]//Proceedings of American Geophysical Union, Fall Meeting 2007. Washington, DC: American Geophysical Union, 2007.
[11] Cook A, Goldberg D. Stress and gas hydrate-filled fracture distribution, Krishna-Godavari basin, India[C]//Proceedings of the 6th International Conference on Gas Hydrate. Vancouver, British Columbia, 2008.
[12] Liu T, Liu X W. Identification of morphologies of gas hydrate distribution based on AVA analysis [J]. Geophysics, 2018, 83(3): B143-B154. doi: 10.1190/geo2017-0072.1
[13] Yang S X, Zhang G X, Zhang M, et al. A complex gas hydrate system in the Dongsha area, South China Sea: results from drilling expedition GMGS2[C]//Proceeding of the 8th International Conference on Gas Hydrate. Beijing: China Geological Survey, 2014.
[14] Lee M W, Collett T S. Gas hydrate and free gas saturations estimated from velocity logs on hydrate ridge, offshore Oregon, USA[M]//Tréhu A M, Bohrmann G, Torres M E, et al. Proceedings of the Ocean Drilling Program, Scientific Results. Texas College Station, 2006.
[15] 戴丹青, 刘学伟. 根据BSR界面RVF特性判断水合物的赋存状态[C]//2015年“海洋地质、矿山资源与环境”学术研讨会论文集. 广州: 中国地质学会, 中国海洋学会, 中国矿物岩石地球化学学会, 广东省地质学会, 2015. DAI Danqing, LIU Xuewei. Identification of hydrate occurrence state according to the characteristics of RVF at BSR interface[C]//Conference on Marine Geology & Mining Resources and Environment. 2015.
[16] Lee M W, Collett T S. Characteristics and interpretation of fracture-filled gas hydrate – An example from the Ulleung Basin, East Sea of Korea [J]. Marine and Petroleum Geology, 2013, 47: 168-181. doi: 10.1016/j.marpetgeo.2012.09.003
[17] Liu T, Liu X W, Zhu T Y. Joint analysis of P-wave velocity and resistivity for morphology identification and quantification of gas hydrate [J]. Marine and Petroleum Geology, 2020, 112: 104036. doi: 10.1016/j.marpetgeo.2019.104036
[18] Sriram G, Dewangan P, Ramprasad T, et al. Anisotropic amplitude variation of the bottom-simulating reflector beneath fracture-filled gas hydrate deposit [J]. Journal of Geophysical Research, 2013, 118(5): 2258-2274.
[19] Liu T, Liu X W. Identifying the morphologies of gas hydrate distribution using P-wave velocity and density: a test from the GMGS2 expedition in the South China Sea [J]. Journal of Geophysics and Engineering, 2018, 15(3): 1008-1022. doi: 10.1088/1742-2140/aaaba1
[20] Daigle H, Dugan B. Origin and evolution of fracture-hosted methane hydrate deposits [J]. Journal of Geophysical Research, 2010, 115(B11).
[21] 胡高伟. 南海沉积物的水合物声学特性模拟实验研究[D]. 中国地质大学博士学位论文, 2010. HU Gaowei. Experimental study on acoustic responses of gas hydrates to sediments from South China Sea[D]. Doctor Dissertation of China University of Geosciences, 2010.
[22] 林霖, 梁劲, 郭依群, 等. 利用声波速度测井估算海域天然气水合物饱和度[J]. 测井技术, 2014, 38(2):234-238. [LIN Lin, LIANG Jin, GUO Yiqun, et al. Estimating saturation of gas hydrates within marine sediments using sonic log data [J]. Well Logging Technology, 2014, 38(2): 234-238. [23] Lee M W, Collett T S. Gas hydrate saturations estimated from fractured reservoir at Site NGHP-01-10, Krishna-Godavari Basin, India [J]. Journal of Geophysical Research, 2009, 114(B7): B07102.
[24] Sha Z B, Liang J Q, Zhang G X, et al. A seepage gas hydrate system in northern South China Sea: Seismic and well log interpretations [J]. Marine Geology, 2015, 366: 69-78. doi: 10.1016/j.margeo.2015.04.006
[25] Helgerud M B, Dvorkin J, Nur A, et al. Elastic-wave velocity in marine sediments with gas hydrates: effective medium modeling [J]. Geophysical Research Letters, 1999, 26(13): 2021-2024. doi: 10.1029/1999GL900421
[26] Ecker C. Seismic characterization of methane hydrate structures[D]. Doctor Dissertation of Stanford University, 1998.
[27] Nur A, Mavko G, Dvorkin J, et al. Critical porosity: a key to relating physical properties to porosity in rocks [J]. The Leading Edge, 1998, 17(3): 357-362. doi: 10.1190/1.1437977
[28] Dvorkin J, Nur A. Rock physics for characterization of gas hydrates[M]//Howell D G. The Future of Energy Gases. Washington: United States Government Printing Office, 1993.
[29] Dvorkin J, Prasad M, Sakai A, et al. Elasticity of marine sediments: Rock physics modeling [J]. Geophysical Research Letters, 1999, 26(12): 1781-1784. doi: 10.1029/1999GL900332
[30] Lee M W. Biot-Gassmann theory for velocities of gas hydrate-bearing sediments [J]. Geophysics, 2002, 67(6): 1711-1719. doi: 10.1190/1.1527072
[31] Hill R. The elastic behaviour of a crystalline aggregate [J]. Proceedings of the Physical Society. Section A, 1952, 65(5): 349-354. doi: 10.1088/0370-1298/65/5/307
[32] Lee M W, Waite W F. Estimating pore-space gas hydrate saturations from well log acoustic data [J]. Geochemistry, Geophysics, Geosystems, 2008, 9(7): Q07008.
[33] Mindlin R D. Compliance of elastic bodies in contact [J]. Journal of Applied Mechanics, 1949, 16: 259-268.
[34] White J E. Seismic Waves: Radiation, Transmission, and Attenuation[M]. New York: McGraw Hill, 1965.
[35] Thomsen L. Weak elastic anisotropy [J]. Geophysics, 1986, 51(10): 1954-1966. doi: 10.1190/1.1442051
-
期刊类型引用(4)
1. 王云龙，邢兰昌，魏伟，韩维峰，朱作飞，苏丕波. 基于多场耦合数值模型的含水合物多孔介质声学特性：骨架颗粒排列和形状的影响. 新能源进展. 2025(01): 7-16 . 
百度学术
2. 徐卫平，丁拼搏，张峰，狄帮让，蔡志光，梅璐璐. 天然气水合物岩石物理实验研究进展. 石油物探. 2023(06): 1016-1029 . 百度学术
3. Yong-chao Zhang，Le-le Liu，Gao-wei Hu，Qing-tao Bu，Cheng-feng Li，Zheng-cai Zhang，Jian-ye Sun，Chang-ling Liu. Formation mechanism, experimental method, and property characterization of grain-displacing methane hydrates in marine sediment: A review. China Geology. 2022(02): 345-354 . 必应学术
4. 赵金环，刘昌岭，邹长春，陈强，孟庆国，刘洋，卜庆涛. 基于ERT技术的含水合物沉积物可视化探测模拟实验. 海洋地质与第四纪地质. 2021(06): 206-212 . 本站查看
其他类型引用(0)
下载:
计量
- 文章访问数: 2593
- HTML全文浏览量: 389
- PDF下载量: 51
- 被引次数: 4
