Simultaneous migration of primary and free surface multiples: modeling data analysis
-
摘要: 基于逆时偏移互相关成像条件,一次反射波与自由表面多次波联合偏移成像可以提供更宽的地下照明成像,以弥补一次反射波覆盖不足,同时不需要预测分离多次波,但是,在成像过程中也引入了偏移假象。首先对一次反射波与自由表面多次波联合偏移成像条件进行分析,通过对模拟数据成像结果分析,提出利用多次波信息进行成像,需要用震源子波和相位反转的地震记录作为逆时偏移中的源端波场做正向传播,原始地震记录作为检波端波场做反向传播,方可获得具有自由表面多次波成像贡献的结果。数值试验结果表明,尽管一次反射波与自由表面多次波联合逆时偏移可以提供更宽的地下照明成像,但是,随着自由表面多次波能量的增强,偏移假象也随之增强;当自由表面多次波能量减弱时,尽管偏移假象相应减弱,但是自由表面多次波对宽角照明成像贡献也随之减弱。因此,一次反射波与自由表面多次波联合偏移成像需要更深入研究。Abstract: Under the condition of reverse time migration and cross correlation imaging, simultaneous migration images of primary and free surface multiples can provide wider underground illumination to make up for the insufficient coverage of the reflections, Therefore, it is not necessary to predict and separate multiples. However, migration artifacts may also be introduced during the process of joint imaging. In this paper, we firstly analyzed the simultaneous migration imaging conditions. Imaging with multiples information needs to use the source wavelet and reverse phase of seismic records as the source side wave field in the reverse-time migration and forward propagate, and the original seismic record as detection side wave field and back propagate, will obtain relative fidelity amplitude imaging results. The results of numerical experiments show that, although the simultaneous reverse time migration imaging of primary and free surface multiples based on cross-correlation imaging condition can provide wider underground illumination, the migration artifacts is also enhanced with the increase in the energy of free surface multiples. When the energy of multiples becomes weak, the intensity of wide-angle illumination by free surface multiples is also weakened, and therefore the simultaneous migration imaging of primary and free surface multiples needs to be further studied.
-
在海洋地震勘探中,由于海水与空气之间的波阻抗差异很大,会形成强烈的自由表面多次波,作为一种规则噪音严重影响了地震速度模型建立与地震成像质量,如何压制这种多次波是过去数十年里海洋地震数据处理中的重点与难点[1]。但是,从地震波传播路径来看,自由表面多次波是一次反射波经海面反射后继续向下传播,然后再次被海底下地层反射而记录到的信息,自由表面多次波相比一次反射波来讲,具有更宽的覆盖区域,提供了比一次反射波更宽的照明[2, 3],合理利用这种多次波能量会拓宽成像孔径,提高地下成像质量。因此,近十多年来,人们提出把多次波作为有效信号加以利用,为复杂地下构造成像提供照明补偿[4-6],有利于提高地震成像质量。目前,自由表面多次波成像有以下3种方法:
(1) 首先进行自由表面多次波分离[7-12],将分离出的多次波通过Schuster提出的地震波干涉法转换为一次反射波[3],这样,多次波成像问题就转化为常规一次反射波成像[13-15]。
(2) 同样,首先进行自由表面多次波分离,利用Liu等人提出的多次波逆时偏移方法[16],把包含一次反射波和自由表面多次波地震记录作为源端波场进行正向传播,而把分离出的自由表面多次波作为检波段波场进行反向传播,利用互相关成像条件进行多次波成像[16, 17]。
(3) 上述两种方法都需要分离自由表面多次波,为了避免自由表面多次波预测工作,Wang等人基于逆时偏移方法,将震源子波与地震记录作为源端正向传播波场,同时地震记录作为检波端反向传播波场,利用互相关成像条件可以实现一次波与多次波联合偏移成像,这种方法避免了复杂繁琐的分离多次波预测工作,可同时利用一次波和多次波能量拓宽照明孔径[18],提高地震成像质量。
上述第3种自由表面多次波成像方法看似理想,但是,基于互相关成像条件的逆时偏移会产生偏移假象,这种偏移假象在多次波成像中更加突出[19]。例如,利用多次波进行逆时偏移,源端正向传播波场的一次反射波与检波端反向传播波场的一阶多次波互相关得到正确的成像,但是,与反向传播波场的二阶以及更高阶多次波互相关得到了虚假的成像。这种偏移成像可以在角道集进行压制处理[20],或者使用立体成像条件等方法进行压制[21-23],但这些方法往往对初始速度模型的依赖较大,在实际应用中效果有限。压制这种高阶多次波偏移假象最直接的方法是首先分离不同阶次多次波,然后分别对这些多次波进行逆时偏移成像[24, 25],但是如何准确分离不同阶次的多次波具有更大的挑战。一些学者如Wong等人提出利用反演的思想[26],采用最小二乘逆时偏移可以一定程度上消除这些偏移假象[27, 30]。
本文基于逆时偏移成像方法,在不考虑震源端与检波端鬼波前提下,从互相关成像条件出发,分析了自由表面多次波与一次反射波联合偏移成像方法。通过数值实验,首先揭示了利用自由表面多次波进行成像,需要将多次波/地震记录做相位反转处理,方能对宽角照明成像做出贡献;其次定性揭示了随着自由表面多次波能量的增强,基于互相关成像条件逆时偏移产生的偏移假象能量也随之增强,从而影响了偏移成像质量;而随着自由表面多次波能量的减弱,尽管偏移噪音能量随之减弱,但多次波对宽角照明成像的贡献也随之减弱。
1. 一次波与自由表面多次波联合偏移成像原理
地震记录在频率域中表示如下[17]:
$$ \mathit{\boldsymbol{D = XS}} $$ (1) 其中D表示地震记录,S表示震源,X表示地层反射系数或者地层脉冲响应,这样D可以表示为一次反射波与各阶次多次的叠加:
$$ \mathit{\boldsymbol{D = P + }}{\mathit{\boldsymbol{M}}^1} + {\mathit{\boldsymbol{M}}^2} + \cdots \cdots + {\mathit{\boldsymbol{M}}^n} $$ (2) 式中P表示一次反射波,M, M1, M2……分别表示不同阶的自由表面多次波,上角标表示自由表面多次波的阶数。自由表面多次波是一次反射波经过海面多次反射形成,相当于将海面反射点看作虚拟震源,所以多次波又可以如下近似表示:
$$ \mathit{\boldsymbol{M}} = \mathit{\boldsymbol{XD}} $$ (3) 假设子波W是震源S的近似估计,偏移模型近似等价于X, 那么可以得到如下表达[18]:
$$ {\mathit{\boldsymbol{P}}_F} = \mathit{\boldsymbol{XW}} $$ (4) $$ {\mathit{\boldsymbol{M}}_F} = \mathit{\boldsymbol{XD}} $$ (5) $$ {\mathit{\boldsymbol{P}}_F} + {\mathit{\boldsymbol{M}}_F} = \mathit{\boldsymbol{X}}\left( {\mathit{\boldsymbol{W + D}}} \right) $$ (6) 其中PF和MF分别表示地震记录中的一次反射波和自由表面多次波,那么根据互相关成像条件,二者联合逆时偏移可以表示如下:
$$ \boldsymbol{I}\left( \boldsymbol{x} \right)=\int{\left( \boldsymbol{W}_{s}^{F}+\boldsymbol{D}_{s}^{F} \right)\centerdot \left( \boldsymbol{D}_{r}^{B} \right)\text{d}t} $$ (7) 上式中s, r, F和B分别表示源端、检波端、正向传播波场和反向传播波场。在公式(7)中,地震记录和震源子波作为源端波场正向传播,同时地震记录又作为检波端波场反向传播,二者互相关成像,由此可以看出,在无需分离多次波的情况下,直接利用地震记录即可实现一次反射波与自由表面多次波联合成像。为了进一步分析公式(7)的具体含义,将公式(2)带入公式(7)可得:
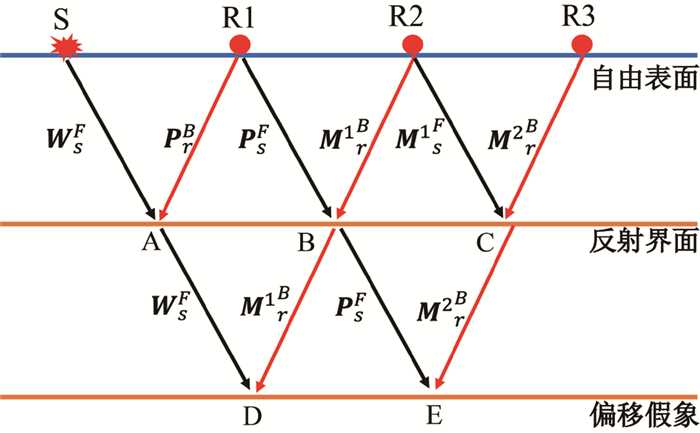
$$ \begin{align} & \boldsymbol{I}\left( \boldsymbol{x} \right)=\int{\left[ \boldsymbol{W}_{s}^{F}\boldsymbol{P}_{r}^{B}+\boldsymbol{P}_{s}^{F}\boldsymbol{M}_{r}^{1\ B} \right.}+\boldsymbol{M}_{s}^{1\ F}\boldsymbol{M}_{r}^{2\ B}+ \\ & \left. \cdots \cdots \right]\text{d}t \\ & \ +\int{\left[ \boldsymbol{W}_{s}^{F}\boldsymbol{M}_{r}^{1\ B}+\boldsymbol{P}_{s}^{F}\left( \boldsymbol{M}_{r}^{2\ B}+\boldsymbol{M}_{s}^{1\ F}\boldsymbol{M}_{r}^{3\ B} \right) \right.}+\left. \cdots \cdots \right]\text{d}t \\ & \ +\int{\left[ \boldsymbol{P}_{s}^{F}\boldsymbol{P}_{r}^{1\ B}+ \right.}\boldsymbol{M}_{s}^{1\ F}+\boldsymbol{M}_{r}^{1\ B}+\left( \boldsymbol{M}_{s}^{2\ F} \right.\boldsymbol{M}_{r}^{1\ B}+\boldsymbol{M}_{s}^{2\ F} \\ & \boldsymbol{M}_{r}^{2\ B}+\left. \cdots \cdots \right]\text{d}t \\ \end{align} $$ (8) 公式(8)等号右边含有3项积分,结合图 1,我们对这3项积分进行分析如下:
第1个积分$\int{\left[ \boldsymbol{W}_{s}^{F}\boldsymbol{P}_{r}^{B}+\boldsymbol{P}_{s}^{F}\boldsymbol{M}_{r}^{1\ B} \right.}+\boldsymbol{M}_{s}^{1\ F}\boldsymbol{M}_{r}^{2\ B}+\left. \cdots \cdots \right]\text{d}t $由3个互相关成像构成:①正向传播震源子波与反向传播一次反射波互相关WSF PrB,成像点为A;②正向传播一次反射波与反向传播一阶自由表面多次波互相关WsFMr1B,成像点为B,由此看出,和一次反射波成像点A相比,多次波成像扩大了照明孔径;③正向传播n阶自由表面多次波与反向传播(n+1)阶自由表面多次波互相关成像Ms1F Mr2B成像点为C,同样,和一次反射波成像点A相比,自由表面多次波成像扩大了照明孔径。上述3项构成了对反射界面的正确成像。
第2个积分$\int{\left[ \boldsymbol{W}_{s}^{F}\boldsymbol{M}_{r}^{1\ B}+\boldsymbol{P}_{s}^{F}\left( \boldsymbol{M}_{r}^{2\ B}+\boldsymbol{M}_{s}^{1\ F}\boldsymbol{M}_{r}^{3\ B} \right) \right.}+\left. \cdots \cdots \right]\text{d}t $为偏移假象,位于真实界面下方。例如,正向传播震源子波与反向传播一阶自由表面多次波互相关WsFMr1B,成像点为D;正向传播一次反射波与反向传播二阶自由表面多次波互相关PsFMr2B,成像点为E。
第3个积分$\int{\left[ \boldsymbol{P}_{s}^{F}\boldsymbol{P}_{r}^{B}+ \right.}\boldsymbol{M}_{s}^{1\ F}+\boldsymbol{M}_{r}^{1\ B}+\left( \boldsymbol{M}_{s}^{2\ F} \right.\boldsymbol{M}_{r}^{1\ B}+\boldsymbol{M}_{s}^{2\ F}\boldsymbol{M}_{r}^{2\ B}+\left. \cdots \cdots \right]\text{d}t $从地震波传播机制分析不会互相关成像,没有实际意义。
本文的重点通过数值试验,研究第1部分与第2部分对地震成像质量的影响。
2. 多次波/地震记录相位对一次反射波与多次波联合偏移成像的影响
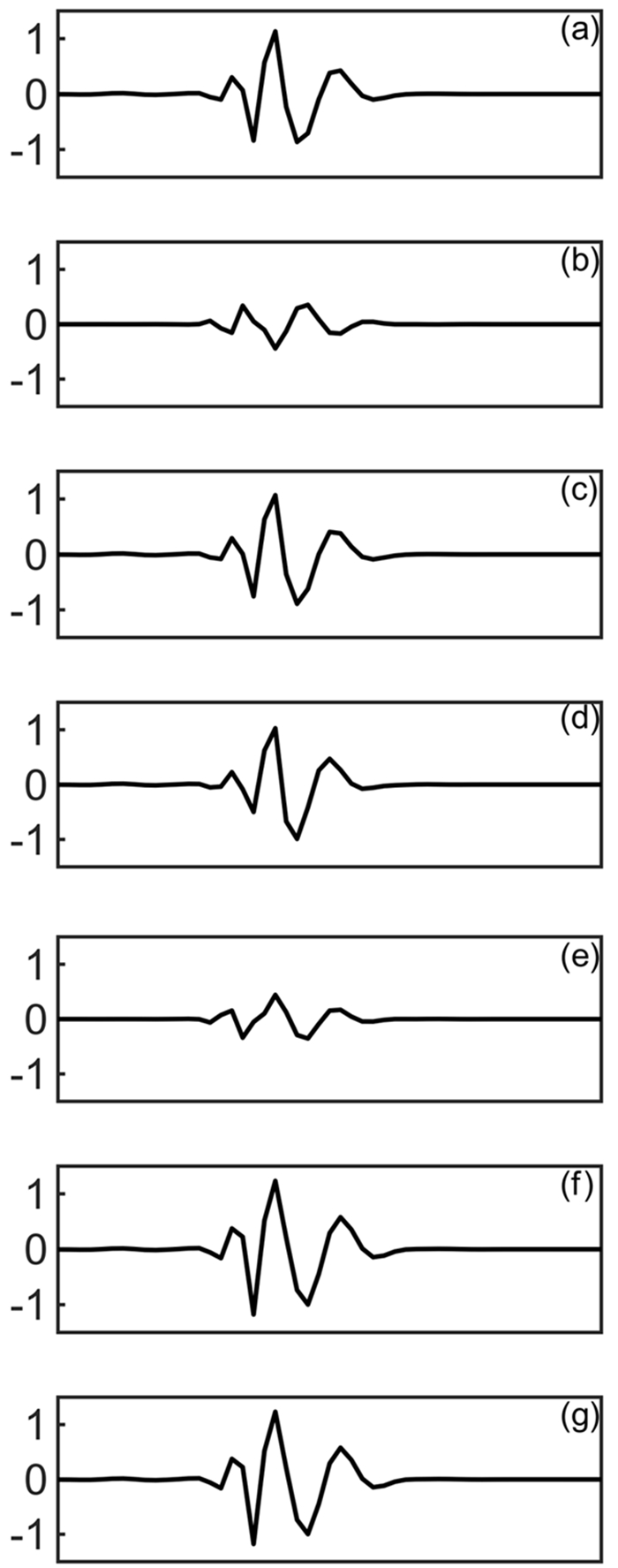
由于空气与海面反射系数近似为-1,所以一阶多次波与一次反射波相位相反,且偶数阶多次波与奇数阶多次波相位相反。那么,在联合偏移成像中,源端正向传播的震源子波与接收端反向传播一次反射波互相关成像的相位,与源端正向传播的一次反射波和接收端反向传播的一阶多次波互相关成像的相位相比,二者正好相反,这样叠加会削弱一次反射波成像质量。为保证自由表面多次反射波能量对联合偏移成像做出贡献,则需要将用于源端波场延拓的地震记录做相位反转处理,即源端波场由震源子波与相位反转的地震记录组成。为验证这个问题,我们设计只有一个反射界面的地质模型,人工合成一次反射波以及与该界面相关的自由表面多次波,利用此合成数据开展地震成像数值实验。图 2显示了各种地震成像结果的单道波形,为了便于对比,对偏移成像结果做了归一化振幅处理。图 2(a)为一次反射波逆时偏移成像单道波形,图 2(b)为多次波逆时偏移成像单道波形,可以看出,图 2(a)与(b)的相位正好相反。图 2(c)为一次反射波与自由表面多次波联合偏移成像单道波形,图 2(d)为(a)与(b)的叠加,可以看出,此叠加波形与(c)波形基本一致。图 2(e)为对多次波做相位反转后的多次波逆时偏移成像单道波形,可以看出图 2(a)与(e)的相位相同,图 2(f)为对多次波做相位反转后的一次反射波与自由表面多次波联合逆时偏移成像单道波形,图 2(g)为(a)与(e)叠加,对比图 2(c)与(f)、图 2(d)与(g)可以看出,对多次波进行相位反转处理后,自由表面多次波能量对一次反射波成像做出了贡献,地震成像振幅能量增强。为叙述方便,以下自由表面多次波逆时偏移成像、一次反射波与多次波联合逆时偏移成像都是指将多次波记录或地震记录做相位反转处理后的成像结果。
3. 数值实验
3.1 单层模型
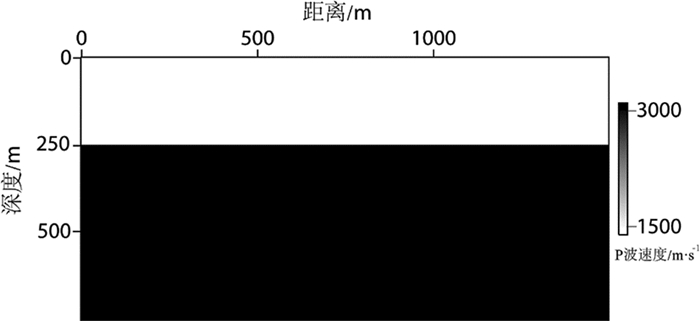
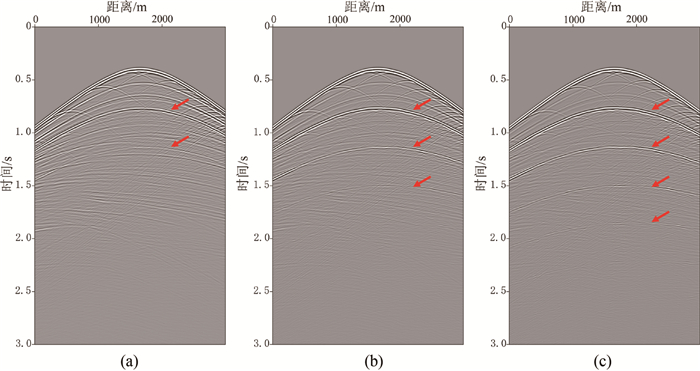
如图 3所示单个反射层模型,上层速度为1500m/s,下层速度为3000m/s,上、下层速度反差达到2倍。模型横向网格数量为301,垂向网格数量为151,空间采样间隔为5m。红点所示为炮点位置,模拟采集20炮记录,点所示为检波点位置,共300个检波点,炮间距和检波点间距均为5m。震源子波为雷克子波,正演模拟结果如图 4所示,分别为一次反射波和三阶自由表面多次波的单炮记录4(a),一次反射波记录4(b)和三阶自由表面多次波记录4(c),可以看出,多次波的能量逐阶减弱。
![]() 图 2 多次波相位对联合偏移的影响a.一次波逆时偏移成像单道波形;b.多次波逆时偏移成像单道波形;c.一次波与多次波联合偏移成像单道波形;d.(a)与(b)的叠加波形;e.多次波相位反转处理后的逆时偏移成像单道波形;f.一次波与多次波相位反转处理后联合偏移成像单道波形;g.(a)与(e)的叠加波形Figure 2. Influence of multiples phase on simultaneous migration(a) Primary RTM singletrace waveform, (b) multiples RTM single trace waveform, (c) simultaneous migration with primary and multiples single trace waveform, (d) the sum of (a) and (b), (e) reverse phase of multiples RTM single trace waveform, (f) simultaneous migration with reverse phase of primary and multiples single trace waveform, (g) summation of (a) and (e)
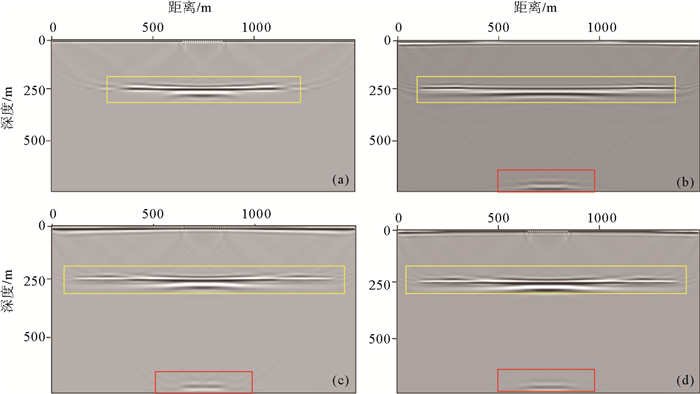
图 2 多次波相位对联合偏移的影响a.一次波逆时偏移成像单道波形;b.多次波逆时偏移成像单道波形;c.一次波与多次波联合偏移成像单道波形;d.(a)与(b)的叠加波形;e.多次波相位反转处理后的逆时偏移成像单道波形;f.一次波与多次波相位反转处理后联合偏移成像单道波形;g.(a)与(e)的叠加波形Figure 2. Influence of multiples phase on simultaneous migration(a) Primary RTM singletrace waveform, (b) multiples RTM single trace waveform, (c) simultaneous migration with primary and multiples single trace waveform, (d) the sum of (a) and (b), (e) reverse phase of multiples RTM single trace waveform, (f) simultaneous migration with reverse phase of primary and multiples single trace waveform, (g) summation of (a) and (e)图 5为逆时偏移成像结果,分别为一次反射波逆时偏移成像5(a),自由表面多次波逆时偏移成像5(b)和一次反射波与自由表面多次波联合逆时偏移成像5(c)。将图 5(a)与5(b)叠加得到5(d),与5(c)比较完全一致。比较图 5黄色框中反射界面的成像结果可以看出,利用多次波成像扩大了照明孔径,弥补了一次反射波成像孔径的不足,但是,引入了偏移假象,如图 5中红框所示,此假象是由于(8)式第2部分积分产生,即正向传播震源子波与反向传播一阶自由表面多次波互相关形成的成像点D或正向传播一次波与反向传播二阶自由表面多次波互相关形成的成像点E(图 1)。
为比较产生多次波的反射界面上、下层速度差异对自由表面多次波成像以及一次波与自由表面多次波联合成像的影响,我们将图 3模型下层速度改为1800m/s,而上层速度保持不变,即上、下层速度反差降低为1.2倍,这个速度反差是上述数值实验的60%,因此,可以定性表示这样的速度结构产生的一次反射波以及自由表面多次波能量是上述数值实验的60%。对此模型分别进行自由表面多次波逆时成像(图 6a)和一次反射波与自由表面多次波联合偏移成像(图 6b)。比较图 6(a)与图 5(b)可以发现,两种情况下多次波对反射界面的照明成像孔径(黄色方框)几乎一致,但是,图 6(a)中的偏移假象范围似乎比图 5(b)中大得多,这是由于此实验中多次波能量相对较弱,多次波对反射界面照明成像的能量也相对减弱,这样,图 6(a)中偏移假象(红色方框)的能量就会显得相对增强(偏移假象范围增大)。上述解释也可以从比较图 5(c)和图 6(b)获得支持,由图 6(b)可以看出,由于多次波能量减弱,一次反射波与自由表面多次波联合偏移成像对反射界面的照明孔径(黄色方框)明显减小,照明范围几乎与图 5(a)中一次波成像范围(黄色方框)一致,自由表面多次波对联合偏移成像贡献减弱。
3.2 复杂模型
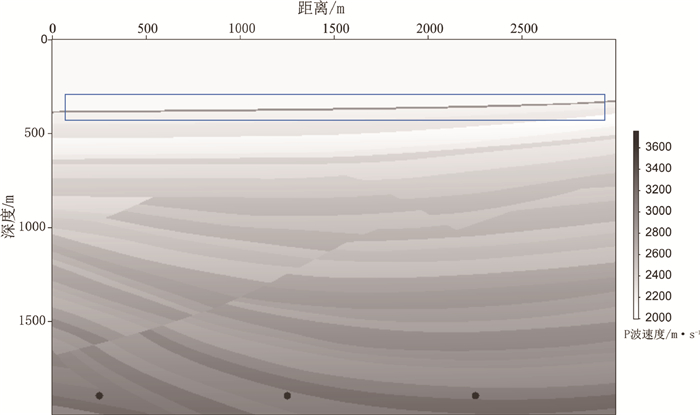
模型截取于Sigsbee 2B速度模型,包含有倾斜地层和断层,模型底部设有3个散射点,如图 7所示。为了考虑自由表面多次波能量强度对联合偏移成像的影响,我们改变蓝框内海底速度,分别取2500、3500和4500m/s,海底上覆水层速度为1500m/s,这样可以模拟不同强度的一次反射波和自由表面多次波,同时模拟采集把震源和检波器均布设在水面,即不考虑震源端与检波端鬼波。
模型在水平方向共有601个网格点,垂向共有401个网格点,空间采样间隔为5m。模拟采集150炮记录,检波点数量为601个,炮间距为20m,检波间距为5m。震源子波同样为雷克子波。图 8为不同海底速度的模拟单炮记录,红色箭头所指为自由表面多次波,可以看出,随着海底速度的增大,自由表面多次波能量增强。
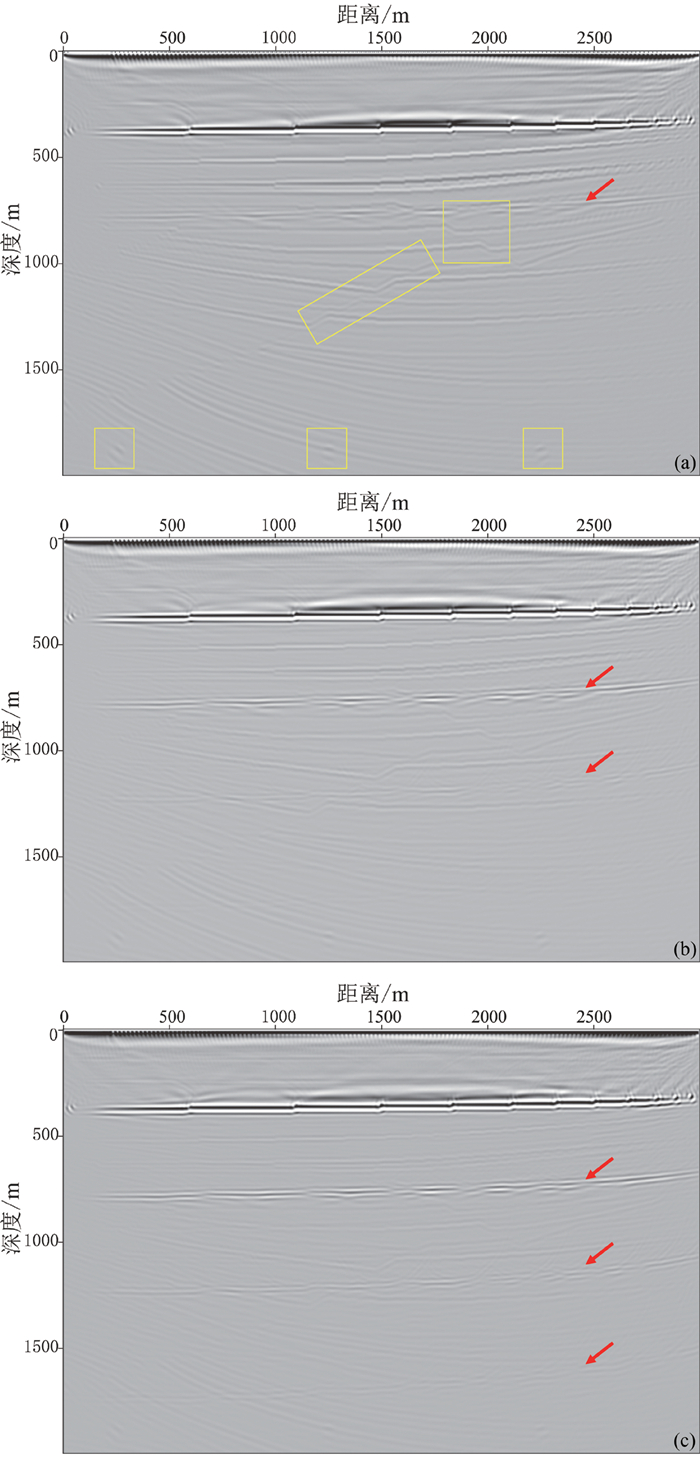
利用上述模拟记录实现一次反射波与自由表面多次波联合逆时偏移成像,偏移叠加成像结果如图 9所示,红色箭头指示偏移假象,对应公式(8)中第2部分积分。图 9(a)显示,当多次波能量较弱时,偏移假象(红色箭头)较弱,一次反射波与自由表面多次波联合偏移对倾斜地层、断层以及散射点(黄色方框)成像较为准确;图 9(b)和(c)显示,随着自由表面多次波能量的增强,偏移假象(红色箭头)能量增强,严重干扰了对地层、断层以及散射点正确成像。
![]() 图 9 Sigsbee 2B截断速度模型一次反射波与多次波联合偏移成像a.海底速度为2500m/s时联合偏移成像;b.海底速度为3500m/s时联合偏移成像;c.海底速度为4500m/s时联合偏移成像Figure 9. Simultaneous imaging with primary and free surface multiples of Truncated Sigsbee 2B velocity model(a) imaging result with 2500m/s seafloor velocity; (b) imaging result with 3500m/s seafloor velocity; (c) imaging result with 4500m/s seafloor velocity
图 9 Sigsbee 2B截断速度模型一次反射波与多次波联合偏移成像a.海底速度为2500m/s时联合偏移成像;b.海底速度为3500m/s时联合偏移成像;c.海底速度为4500m/s时联合偏移成像Figure 9. Simultaneous imaging with primary and free surface multiples of Truncated Sigsbee 2B velocity model(a) imaging result with 2500m/s seafloor velocity; (b) imaging result with 3500m/s seafloor velocity; (c) imaging result with 4500m/s seafloor velocity4. 讨论
数值实验表明,一次反射波与自由表面多次波联合偏移成像可以拓宽地下照明成像孔径,弥补了一次反射波成像孔径的不足,且整个过程避免了复杂繁琐的多次波分离预测问题。将地震记录作为源端波场延拓时,需要对地震记录做相位反转处理,以保证一次反射波与多次波联合偏移对成像的贡献。但是,随着自由表面多次波能量的增强,偏移假象也随之增强。对互相关成像条件分析可以发现,这种偏移假象能量最强的部分是源端正向传播震源子波波场与接收端反向传播一阶多次波波场互相关结果,因此偏移噪音就会增强,由此可见,这种一次反射波与自由表面多次波联合偏移成像方法仅适用于自由表面多次波能量较弱的情形,但是,当自由表面多次波能量较弱时,自由表面多次波对扩大照明成像孔径的贡献也随之减弱,这样联合偏移的价值就会降低。本文只是从理论与数值模拟分析角度研究了水平界面产生的自由表面多次波对地震成像的影响,对于横向起伏较大界面产生的自由表面多次波对地震成像的影响,在理论上很难分析,但是,可以考虑在后续研究中建立一个包含复杂海底的模型,通过数值实验来研究横向起伏较大界面产生的自由表面多次波对地震成像的影响。
5. 结论
基于逆时偏移中互相关成像条件,分析了一次反射波与自由表面多次波成像的基本原理,通过数值实验,提出一次反射波与自由表面多次波联合偏移成像,需要将地震记录做相位反转,并与震源子波一起作为正向传播源端波场,这样自由表面多次波能量方可对一次波成像做出贡献,从而提高地震成像质量。一次反射波与自由表面多次波联合偏移成像中的偏移假象,随着多次波能量的增大而加强,这是一次反射波与自由表面多次波联合偏移方法的局限性,因此不做多次波预测分离的前提条件下,如何直接利用包含多次波的地震记录做联合偏移,拓宽照明成像孔径,从而提高成像质量并压制偏移假象还有待进一步深入研究。
-
图 2 多次波相位对联合偏移的影响
a.一次波逆时偏移成像单道波形;b.多次波逆时偏移成像单道波形;c.一次波与多次波联合偏移成像单道波形;d.(a)与(b)的叠加波形;e.多次波相位反转处理后的逆时偏移成像单道波形;f.一次波与多次波相位反转处理后联合偏移成像单道波形;g.(a)与(e)的叠加波形
Figure 2. Influence of multiples phase on simultaneous migration
(a) Primary RTM singletrace waveform, (b) multiples RTM single trace waveform, (c) simultaneous migration with primary and multiples single trace waveform, (d) the sum of (a) and (b), (e) reverse phase of multiples RTM single trace waveform, (f) simultaneous migration with reverse phase of primary and multiples single trace waveform, (g) summation of (a) and (e)
图 9 Sigsbee 2B截断速度模型一次反射波与多次波联合偏移成像
a.海底速度为2500m/s时联合偏移成像;b.海底速度为3500m/s时联合偏移成像;c.海底速度为4500m/s时联合偏移成像
Figure 9. Simultaneous imaging with primary and free surface multiples of Truncated Sigsbee 2B velocity model
(a) imaging result with 2500m/s seafloor velocity; (b) imaging result with 3500m/s seafloor velocity; (c) imaging result with 4500m/s seafloor velocity
-
[1] Edmund C Reiter, M Nafi Toksoz, Timothy H Keho, et al. Imaging with deep-water multiples [J]. Geophysics, 1991, 56(7): 1081-1086. doi: 10.1190/1.1443119
[2] Christopher D Manuel, Norm F Uren. Pre-stack depth migration of seismic multiples [J]. Exploration Geophysics, 2000(31): 328-332.
[3] Yu J, Schuster G. Joint migration of primary and multiple reflections in RVSP data [C]// Annual International Meeting, SEG, Expanded Abstracts. 2002: 2373-2376.
[4] Muijs R, Robertsson A J O, Holliger K. Prestack depth migration of primary and surface-related multiple reflections: Part I - Imaging [J]. Geophysics, 2007, 72(2):3953-3957.
[5] Remco Muijs, Johan O A Robertsson, Klaus Holliger. Prestack depth migration of primary and surface-related multiple reflections: Part II - Identification and removal of residual multiples [J]. Geophysics, 2007, 72(2): S71-S76. doi: 10.1190/1.2424544
[6] Youn O K, Zhou H W. Depth imaging with multiples [J]. Geophysics, 2001, 18(1): 246-255.
[7] Verschuur D J. Adaptive surface-related multiple elimination [J]. Geophysics, 1992, 57(9):1166-1177. doi: 10.1190/1.1443330
[8] Berkhout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion; Part I, Theoretical considerations [J]. Geophysics, 1997, 62(5):1586-1595. doi: 10.1190/1.1444261
[9] Verschuur D J, Berkhout A J. Estimation of multiple scattering by iterative inversion; Part II, Practical aspects and examples [J]. Geophysics, 1997, 62(5):1596-1611. doi: 10.1190/1.1444262
[10] Berkhout A J, Verschuur D J. Transformation of multiples into primary reflections [C]// 73th Annual International Meeting, SEG, Expanded Abstracts. 2003: 1925-1928.
[11] Verschuur D J, Berkhout A J. Transforming multiples into primaries: experience with field data [C]// 75th Annual International Meeting, SEG, Expanded Abstracts. 2005: 2103-2106.
[12] vanDedem E J, Verschuur D J. 3D surface-related multiple prediction, an inversion approach [J]. Geophysics, 2005, 70(3): V31-V43. doi: 10.1190/1.1925752
[13] Berkhout A, Verschuur D. Imaging of multiple reflections[J]. Geophysics, 2006, 71(4):SI209-SI220. doi: 10.1190/1.2215359
[14] Jiang Z J, Sheng J Yu, Schuster G T, et al. Migration methods for imaging different-order multiples [J]. Geophysical Prospecting, 2007, 55: 1-19. doi: 10.1111/j.1365-2478.2006.00598.x
[15] Guitton A. Shot-profile migration of multiple reflections [C]// 72th Annual International Meeting, SEG, Expanded Abstracts. 2002: 1296-1299.
[16] Edip Baysal, Dan D Kosloff, John W C Sherwood. Reverse time migration [J]. Geophysics, 1983, 48(11): 1514-1524. doi: 10.1190/1.1441434
[17] Liu Y K, Chang X, Jin D G, et al. Reverse time migration of multiples for subsalt imaging [J]. Geophysics, 2011a, 76(5): WB209-WB216. doi: 10.1190/geo2010-0312.1
[18] Wang Yibo, Chang Xu, Hu Hao. Simultaneous reverse time migration of primaries and free-surface related multiples without multiple prediction [J]. Geophysics, 2014, 79(1): S1-S9. doi: 10.1190/geo2012-0450.1
[19] 刘学建, 刘伊克.表面多次波最小二乘逆时偏移成像[J].地球物理学报, 2016, 59(9): 3354-3365. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqwlxb201609019 LIU Xuejian, LIU Yike. Least-squares reverse-time migration of surface-related multiples [J]. Chinese Journal of Geophysics. 2016, 59(9): 3354-3365. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqwlxb201609019
[20] Wang Y Y, Zheng L, Zhang X, et al. Reverse time migration of multiples: Eliminating migration artifacts in angle domain common image gathers [J]. Geophysics, 2014, 79(6): S263-S270. doi: 10.1190/geo2013-0441.1
[21] Sava P. Stereographic image condition for wave-equation migration[J].Geophysics, 2007, 72(6):A87-A91. doi: 10.1190/1.2781582
[22] Li Z N, Li Z C, Wang P. Joint migration of primaries and surface-related multiples based onstereographic imaging condition [C]// SEG Technical Program Expanded Abstracts. 2015: 4585-4589.
[23] Li Z N, Li Z C, Wang P, et al. One-way wave-equation migration of multiples based on stereographic imaging condition [J]. Geophysics, 2017, 82(6):1-47. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=386171ad96fac7c720324edbadeb5117
[24] Li Z N, Li Z C, Wang P, et al. Reverse time migration of multiples based on different-order multiple separation [J]. Geophysics, 2017, 82(1): S19-S29. doi: 10.1190/geo2015-0710.1
[25] Liu Y K, Liu X J, et al.Least-squares reverse time migration using controlled-order multiple reflections [J]. Geophysics, 2016, 81(5): S347-S357. doi: 10.1190/geo2015-0479.1
[26] Wong M, Biondi B, Ronen S. Imaging with primaries and free surface multiples by joint least-squares reverse time migration [J]. Geophysics, 2015, 80(6): S223-S235. doi: 10.1190/geo2015-0093.1
[27] Zhang D L, Schuster G T. Least- squares reverse time migration of multiples [J].Geophysics, 2014, 79(1): S11-S21. doi: 10.1190/geo2013-0156.1
[28] Tu N, Herrmann F J. Fast imaging with surface-related multiples by sparse inversion [J]. Geophysical Journal International, 2015, 201(1): 304-317. doi: 10.1093/gji/ggv020
[29] Tu N, Herrmann F J. Fast least-squares imaging with surface-related multiples: Application to a North Sea data set [J]. The Leading Edge, 2015(6): 788-793.
[30] He R, Schuster G. Least-squares migration of both primaries and multiples [C]// SEG Technical Program Expanded Abstracts. 2003: 1035-1038.



 下载:
下载: