MATHEMATICAL SIMULATION FOR SUBMARINE GAS HYDRATE FORMATION: UPON THE ASSUMPTION OF UPWARD ADVECTION OF METHANE-BEARING POREWATER
-
摘要: 为深入了解深部上升流体供应甲烷的海底沉积环境中天然气水合物的形成和聚集过程,综合沉积作用、深部上升甲烷流体的对流和扩散作用、甲烷溶解度控制水合物形成等物理过程,建立了天然气水合物形成过程的数学模型,研究水合物在空间和时间尺度上的形成过程。模型通过3个无量纲参数(沉积压实引起的孔隙流体对流与扩散的比率Pe1、深部流体向上对流传输与扩散的比率Pe2、深部上升流体的甲烷含量$\widetilde C_{m, ext}^{_{_{\rm{l}}}}$),形象地描述了天然气水合物在海底沉积中的聚集过程。数值模拟研究表明,天然气水合物首先在稳定带内上部某一位置形成,随后由于沉积作用向下延伸而在稳定带底部形成水合物;水合物演化时间与Pe1、Pe2及$\widetilde C_{m, ext}^{_{_{\rm{l}}}}$呈负相关;水合物含量与Pe1、$\widetilde C_{m, ext}^{_{_{\rm{l}}}}$负相关,而与Pe2正相关。甲烷溶解度曲线对水合物形成和分布有重要影响,但深部上升流体的甲烷含量、上升流体的通量决定了整个水合物系统甲烷量的输入和输出,是海底天然气水合物形成的主要控制因素。Abstract: Sea bottom gas hydrate (GH) may be formed by porewater advecting upward from deep. In order to understand this process, we developed a non-dimensional mathematical model, combining together the sedimentary process, methane transporting by convection and diffusion of fluid upward, and methane solubility, for study of GH formation and accumulation in a temporal and spatial framework. The model describes the process of GH formation and accumulation with 3 dimensionless parameters, Pe1, Pe2, $\widetilde C_{m, ext}^{_{_{\rm{l}}}}$, which represents respectively the sedimentary process, porewater advection upward from deep and methane content in the fluid. GH emerges in the upper gas hydrate stability zone (GHSZ) first, then grows downward within the continuous sedimentary deposits, and extends eventually to the base of GHSZ. There is a negative correlation between GH evolution time and the three parameters of Pe1, Pe2, $\widetilde C_{m, ext}^{_{_{\rm{l}}}}$, and between GH concentration and Pe1, $\widetilde C_{m, ext}^{_{_{\rm{l}}}}$, but a positive correlation between GH concentration, evolution time and upward methane flux (Pe2 and $\widetilde C_{m, ext}^{_{_{\rm{l}}}}$). The methane solubility influences greatly on the GH formation and distribution. But the simulation results suggest that both the methane concentration of fluid flow from deep and its flux control the methane inputs and outputs of the hydrate system. They are not included in the solubility-curve. So we propose the methane concentration of porewater upward and its flux as controlling factors.
-
大洋钻探计划(Ocean Drilling Program, ODP)164航次研究指出,海底天然气水合物是一种动态的甲烷储库,建立其时间和空间尺度上的演化过程,了解其形成快慢和分布是未来研究的挑战[1]。目前国内外对天然气水合物赋存及分布的主控因素尚缺乏全面而系统的认识[2]。海底水合物藏是甲烷动态输入和输出的复杂系统[3-4],甲烷是如何产生,如何传输,又是如何在沉积层中形成天然气水合物的过程,目前还知之不多[4]。水合物的资源量和分布可通过一些间接技术来量化[3, 5],如保压取样、孔隙流体地球化学、测井和地震属性等。但这些方法只能给出一些静态参量,并不能描述水合物是如何形成的,或者控制水合物聚集的过程。以系统的思想、综合的方法开展天然气水合物演化过程中物理化学响应、成藏要素的耦合作用等已成为水合物系统研究的趋势[2],其中数值模拟研究愈来愈受到重视。
20世纪90年代初,深部含有甲烷的上升流体进入水合物稳定带而形成水合物的思想已经形成[6]。在取得丰富的地球物理、地球化学间接指标和钻探获取水合物样品基础上,近十余年来欧美国家数值模拟研究在水合物的形成速率、海底上升流体通量大小的影响、甲烷含量的影响、沉积环境的影响等方面都提高了人们对天然气水合物形成过程的认识。Rempel和Buffett[7]通过物质和能量平衡方程,计算了上升流体传送甲烷形成水合物的速率。Rempel和Buffett[8], Xu和Ruppel[9]又考虑了溶解甲烷在孔隙流体中的扩散作用和原位生物甲烷的产生,给出了水合物的空间分布。Zatsepina和Buffett[10]研究指出甲烷于海底沉积中溶解度随深度指数增大,Davie和Buffett[11]在此基础上构建了水合物、自由气体和溶解甲烷的质量平衡方程式,计算表明了沉积速率、甲烷供应率的关键影响。Bhatnagar等[12]通过甲烷在热力学平衡条件下的溶解度和物质守恒方程模拟了水合物在海底沉积中的分布规律,以无量纲变量形式给出了描述。Haacke等[13, 14]仅关注自由气体带(忽略可移动气相)的形成,通过含甲烷上升流体的对流扩散方程的有限差分运算,得出自由气体带的稳定与甲烷溶解度在稳定带以下的特性有关,并据此提出了水合物形成的甲烷溶解度曲线变化机制。
数值模拟研究中,以往的研究主要针对某一具体环境或大洋钻探站位作为数值模拟的对象,具有普适性的无量纲化模拟研究还较少[12];且聚焦于模拟的终态与实际水合物分布的吻合,而水合物形成过程的特点还少有涉及。水合物的甲烷来源有热成降解和生物成因两种,而一般认为微生物作用降解产生的甲烷不足以形成大量水合物[11, 12, 15]。本文建立模型研究海底沉积深部上升流体供应甲烷的环境中天然气水合物的形成过程。模型综合沉积作用、深部上升甲烷流体的对流和扩散作用、甲烷三相平衡溶解度控制水合物形成等物理过程。最后对模型中的参数进行无量纲化,以求用具有普适性的模型和最简单的参数来研究水合物在空间和时间尺度上的形成过程,量化水合物在海底沉积中的垂直分布,深化水合物的成藏机制。
1. 数学模型
天然气水合物在其热力学稳定带中当甲烷供应充足的时候才会形成。甲烷在海底沉积孔隙水中气液固之间的相平衡非常重要,它决定了水合物存在需要的最小的甲烷浓度。在稳定域内只有当溶解于沉积孔隙水中的甲烷气体浓度超过其饱和度时,水合物才会从孔隙流体中析出形成。本文应用Davie等[16]提出的简单实用的拟合公式来计算海底沉积中甲烷的溶解度。沉积压实及其引起的孔隙流体运动引用Bhatnagar等[12]的研究结果。在上述基础上以连续方程为基础,综合深部流体以对流和扩散方式向稳定带内传输甲烷的过程以及海底沉积层环境(沉积速率、孔隙度、甲烷溶解度等)建立甲烷的三相物质平衡方程,在一维方向上表示为:
$$ \begin{array}{*{20}{l}} {\frac{\partial }{{\partial t}}\left( {\phi \left( {1 - {S_{\rm{h}}} - {S_{\rm{g}}}} \right){\rho _1}C_m^l + \phi {S_{\rm{h}}}{\rho _{\rm{h}}}C_m^h + \phi {S_{\rm{g}}}{\rho _{\rm{g}}}C_m^g} \right) + }\\ {\nabla \cdot \left( {\phi \left( {1 - {S_{\rm{h}}} - {S_{\rm{g}}}} \right)\left( {{V_{l,ext}} + {V_{l,sed}}} \right){\rho _l}C_m^l + \phi {S_h}{V_s}{\rho _h}C_m^h + \phi {S_{\rm{g}}}{V_s}{\rho _{\rm{g}}}C_m^g} \right) = }\\ {\nabla \cdot \left( {\phi \left( {1 - {S_{\rm{h}}} - {S_{\rm{g}}}} \right){D_m}{\rho _l}\frac{{\partial C_m^l}}{{\partial z}}} \right)} \end{array} $$ (1) 式中,φ表示孔隙度;Sh、Sg代表水合物、气相甲烷在沉积孔隙中的体积分数;ρl、ρh、ρg为孔隙流体、水合物、气相甲烷的质量体积浓度(g/L);Vl,sed、Vl,ext分别为沉积引起的孔隙流体速度和深部上升流体速度(mm/a);Cml、Cmh、Cmg分别表示甲烷在孔隙流体、水合物、自由气体中的质量体积浓度(g/L);Dm为甲烷在孔隙流体中的扩散系数(m2/s);Vs为沉积速率(cm/ka)。
偏微分方程(1)即为求解水合物形成过程中其体积变化的控制方程。式中等式左边对时间求偏导的第一项表达式为甲烷在沉积孔隙中气液固三相积累的总量随时间的变化,第二项代表甲烷由于孔隙流体对流传输及沉积携带水合物或游离气体总的甲烷通量。等式右边最后一项为甲烷在孔隙流体中的扩散。为使模型具有普适性并以最少的参数给出描述,对方程(1)进行无量纲化。方程无量纲化过程中,深度z以BSR深度(Lz)进行归一化;甲烷质量浓度Cml、Cmh、Cmg以BSR处的甲烷溶解度Cm,eqbl为参考归一化;时间t以t0=Lz2/Dm归一化;密度ρl、ρh、ρg以ρl为参考进行归一化;沉积通量Us以沉积压实引起的孔隙流体通量Ul,sed无量纲化,具体如下:
$$ \begin{array}{l} \widetilde{z} = \frac{z}{{{L_z}}},\widetilde t = \frac{t}{{\frac{{L_z^2}}{{{D_m}}}}},{\widetilde U_s}{\rm{ = }}\frac{{{U_s}}}{{{U_{l,sed}}}}\\ {\widetilde \rho _l} = \frac{{{\rho _l}}}{{{\rho _l}}} = 1,{\widetilde \rho _h} = \frac{{{\rho _h}}}{{{\rho _l}}},{\widetilde \rho _g} = \frac{{{\rho _g}}}{{{\rho _l}}}\\ \widetilde C_m^{_l} = \frac{{C_m^l}}{{C_{m,eqb}^l}},\widetilde C_m^{_h} = \frac{{C_m^h}}{{C_{m,eqb}^l}},\\ \widetilde C_m^{_g} = \frac{{C_m^g}}{{C_{m,eqb}^l}},\widetilde C_m^{_{\rm{l}}} = \frac{{C_m^l}}{{C_{m,eqb}^l}} \end{array} $$ (2) 方程(1)经上述简化,无量纲形式为:
$$ \begin{array}{*{20}{l}} {\frac{\partial }{{\partial {\rm{ }}\widetilde t}}\left( {\frac{{1 + r\widetilde \varphi }}{r}\left( {\left( {1 - {S_h} - {S_g}} \right)\widetilde C_m^{_l} + {S_h}{{\widetilde \rho }_h}\widetilde C_m^{_h} + {S_g}{{\widetilde \rho }_g}\widetilde C_m^{_g}} \right)} \right) + }\\ {\frac{{1 + r}}{r}\frac{\partial }{{\partial {\rm{ }}\widetilde z}}\left[ {\left( {{\rm{P}}{{\rm{e}}_{\rm{2}}} + {\rm{P}}{{\rm{e}}_{\rm{1}}}} \right)\left( {1 - {S_h}} \right)\widetilde C_m^{_l} + {\rm{P}}{{\rm{e}}_{\rm{1}}}\widetilde Us\frac{{1 + r\widetilde \varphi }}{{r\left( {1 - \widetilde \varphi } \right)}}\left( {{S_h}{{\widetilde \rho }_h}\widetilde C_m^{_h} + {S_g}{{\widetilde \rho }_g}\widetilde C_m^{_g}} \right)} \right] = }\\ {\frac{\partial }{{\partial {\rm{ }}\widetilde z}}\left( {\frac{{1 + r\widetilde \varphi }}{r}\left( {1 - {S_h} - {S_g}} \right)\frac{{\partial {\rm{ }}\widetilde C_m^{_l}}}{{\partial {\rm{ }}\widetilde z}}} \right)} \end{array} $$ (3) 其中$r = \left( {1 - {\varphi _\infty }} \right)/{\varphi _\infty }, \widetilde \varphi = \left( {\varphi - {\varphi _\infty }} \right)/\left( {1 - {\varphi _\infty }} \right)$(φ为海底沉积孔隙度,φ∞为最小孔隙度)。Us、Ul,sed、Ul,ext(Us=Vs·(1-φ), Ul,sed=Vl,sed·φ, Ul,ext=Vl,ext·φ)为沉积颗粒、沉积压实引起的孔隙流体、深部上升流体的通量(m/s)。佩克莱数(Peclet number)Pe1=Ul,sedLz/Dm,Pe2=Ul,extLz/Dm(其中Lz为水合物稳定带的厚度),Pe1为沉积压实引起的孔隙流体对流与扩散的比率,Pe2为深部流体向上对流传输与扩散的比率。随着佩克莱数的增大,扩散所占比例减少,对流输运的比例增大。
甲烷由深部上升流体以对流扩散方式向稳定带内传输,因此孔隙流体通量是一个非常重要的参数,其决定了甲烷的传输速度。孔隙流体通量为Uf=Uf,sed+Uf,ext,Bhatnagar等[12]分析推导后得出了${U_f} = {U_{f, sed}} + {U_{f, sxt}} - {U_s}{S_h}C_\omega ^h{\widetilde \rho _h}\varphi /\left( {1 - \varphi } \right)$,然后又以Uf,sed+|Uf,ext|为参考值对孔隙流体进行无量纲化,使得方程极为复杂。直接应用Uf=Uf,sed+Uf,ext代表孔隙流体的通量修正并简化了Bhatnagar等[12]的无量纲化方法。经过上述无量纲化后,方程(3)以参数Pe1、Pe2、$\widetilde C_{m, ext}^{_{_{\rm{l}}}}$来考察沉积孔隙中溶解甲烷和固体水合物含量($\widetilde C_m^{_l}$、$\widetilde C_m^{_h}$)的时空变化。初始条件:$\widetilde C_m^{_l}\left( {\widetilde z, 0} \right) = 0$,边界条件:$\widetilde C_m^{_l}\left( {0, \widetilde t} \right) = 0, \widetilde C_{m, ext}^{_l}\left( {\widetilde D, \widetilde t} \right) = \widetilde C_{m, ext}^{_l}$。
采用Crank-Nicolson加权隐式差分格式对方程(3)进行离散化,最后编程求解。水合物稳定带的厚度Lz标记为无量纲参考单位1,在单位空间尺度上划分100份,即以0.01单位长度$\widetilde z$为空间步长;单位时间尺度上划分104份,即以10-4单位时间长度$\widetilde t$为时间步长。由于水合物稳定带的厚度一般在百米级别,因此空间步长在1 m左右。水合物演化的时间尺度单位以t0=Lz2/Dm为参考,在百万年(Ma)级别[12],因此时间步长约100 a。由于主动大陆边缘较高的深部上升流体速度为1~2 mm/a[6-17],在时间步长内,流体传输距离为厘米级别,比空间步长小一个数量级,因此在满足计算精度的前提下,网格比较合理,若选择更小的网格比将使模拟的时间成倍增长。
2. 参数敏感度分析
模型以Pe1、Pe2、$\widetilde C_{m, ext}^{_{_{\rm{l}}}}$3个参量来考察沉积孔隙中溶解甲烷和固体水合物含量的时空变化。不同的参数及其组合会产生不同的模拟结果,因此,下面将量化各参数对模型的影响。
参数Pe1为沉积压实引起的孔隙流体对流与扩散的比率,代表了海底沉积的快慢。由图 1-A可见水合物的体积随着Pe1增大而减小,仅在0.25到0.3之间稍有增加。即海底沉积速度越慢,沉积引起的水合物层向深部迁移的速度越慢,更多的甲烷以固态的水合物形式留存在了稳定带内,因而水合物的体积愈大。当沉积速率在最高的范围内,形成的水合物通过沉积压实与沉积颗粒一同向深部迁移,使得沉积带来的水合物高于孔隙流体对流和扩散输出的甲烷量,因此,水合物体积稍有增加。水合物形成并在沉积孔隙中保持一定的体积是深部甲烷的对流扩散输入与沉积引起的向下输出双重作用导致的。由图 1-B可见,佩克莱数Pe1对稳定带内水合物形成时间的影响与对水合物生长的影响相似。由前述无量纲化过程中$\widetilde t = t/\left( {L_z^2/{D_m}} \right)$,得出单位时间${\widetilde t_0} \approx 6.4{\rm{Ma}}$。随着Pe1的减小,水合物在整个稳定带内形成的时间跨度变得愈来愈大,当Pe1取值约0.23时,形成时间最小,而当Pe1再增大时,模拟时间稍有增加约3%单位时间${\widetilde t_0}$。即海底的沉积速度越小,由沉积引起的水合物向下的迁移就越小,因此稳定带底部形成水合物的时间跨度则变大,相比最小需要时间,可增加约20%。而当沉积速率较大时,即沉积压实引起的孔隙流体的通量Uf, sed较大,Pe1为正值达到最大,而Pe2向上为负值,致使孔隙流体的向上传输通量变小,也就是甲烷的输入量变小,因此,时间跨度稍微变大。
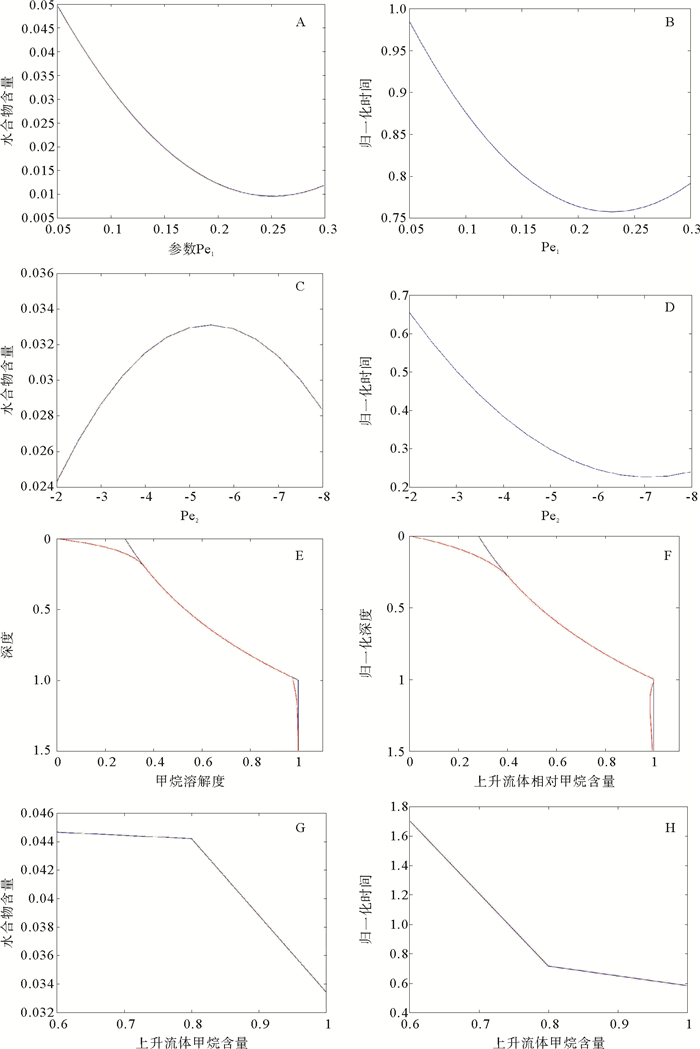
![]() 图 1 模型参数敏感度分析A.水合物含量Sh与Pe1(表征海底沉积的快慢)的关系(Pe2=-2.6,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$, 以最小/最大沉积速率为10/100 cm/ka得出Pe1介于0.05和0.3之间);B.水合物演化时间t与Pe1的关系(Pe2=-2.6,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$);C.水合物含量Sh与Pe2的关系(Pe1=0.1, $\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$);D.水合物演化时间t与Pe2的关系(Pe1=1.0,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$);E.稳定带底部形成水合物时海底沉积中的溶解甲烷量(红色线)与溶解度(蓝色线)的比较(Pe1=1.0,Pe2=-8,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1.0$);F.稳定带底部形成水合物时海底沉积中的溶解甲烷量(红色线)与溶解度(蓝色线)的比较(Pe1=1.0,Pe2=-2.6,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1.0$);G.水合物含量Sh与$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$的关系($\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$代表深部上升流体的甲烷含量, Pe1=1.0,Pe2=-2.6);H.水合物演化时间t与$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$的关系(Pe1=1.0,Pe2=-2.6)Figure 1. Model sensitivity to parameters
图 1 模型参数敏感度分析A.水合物含量Sh与Pe1(表征海底沉积的快慢)的关系(Pe2=-2.6,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$, 以最小/最大沉积速率为10/100 cm/ka得出Pe1介于0.05和0.3之间);B.水合物演化时间t与Pe1的关系(Pe2=-2.6,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$);C.水合物含量Sh与Pe2的关系(Pe1=0.1, $\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$);D.水合物演化时间t与Pe2的关系(Pe1=1.0,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$);E.稳定带底部形成水合物时海底沉积中的溶解甲烷量(红色线)与溶解度(蓝色线)的比较(Pe1=1.0,Pe2=-8,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1.0$);F.稳定带底部形成水合物时海底沉积中的溶解甲烷量(红色线)与溶解度(蓝色线)的比较(Pe1=1.0,Pe2=-2.6,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1.0$);G.水合物含量Sh与$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$的关系($\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$代表深部上升流体的甲烷含量, Pe1=1.0,Pe2=-2.6);H.水合物演化时间t与$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$的关系(Pe1=1.0,Pe2=-2.6)Figure 1. Model sensitivity to parameters参数Pe2为深部流体向上对流传输与扩散的比率,代表了海底沉积深部上升流体的快慢。主动大陆边缘由于板块运动活跃,使得深部上升流体速度较高,如在温哥华外海卡斯卡迪区域,孔隙流体上升速度可达1 mm/a[17]。被动大陆边缘构造活动相对平缓,深部上升流体速度较慢,如在布莱克海台深部流体上升速度仅有0.2 mm/a[15]。换算为佩克莱数Pe2为-2~-8。由图 1-C可见佩克莱数Pe2增大即为深部含甲烷流体上升速度变大,传输至稳定带的甲烷量变大,因此,引起水合物体积的变大。当上升流体速度较大时,如Pe2=-8时,由于甲烷在孔隙流体中的高含量以及孔隙流体的高速度,当稳定带底部形成水合物时,此时才仅用约1/4的单位时间${\widetilde t_0}$(图 1-D),如此短的时间内,甲烷含量为$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$的深部上升流体还未到达稳定带底部(图 1-E),整个稳定带内的水合物形成需要的甲烷均为以溶解形式存在的甲烷的扩散提供的,因此,形成的水合物的体积有所减小,但可预见这一情形下的水合物还会在后期的演化中继续增长。而当取Pe2=-0.1时,超过单位时间${\widetilde t_0}$仍没有水合物开始形成,这也同Xu和Ruppel[9]提出的水合物形成需要某一最小甲烷通量相吻合。由图 1-D可见,佩克莱数Pe2对稳定带内水合物演化时间的影响, 随着Pe2的减小,水合物在整个稳定带内形成的时间跨度变得愈来愈大,当Pe2取值约-7时,形成时间最小,速度再增大,则由于对流作用大于沉积作用使得时间跨度稍微增大。当Pe2再减小时,模拟时间增加明显,从Pe2=-6到Pe2=-2,时间跨度由0.2单位时间${\widetilde t_0}$增加到1.1单位时间${\widetilde t_0}$。即海底沉积深部上升流体速度越小,稳定带底部形成水合物的时间跨度则越大,相比最小需要时间,变化明显。而当上升流体速度较大的时候,即来自底部的对流扩散运移来的甲烷量较大,任一深度处水合物形成的时间都缩小,因此,稳定带底部形成水合物的时间跨度亦减小。
由图 1-H可见参数$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$越小,稳定带底部形成水合物所需要的时间越长,当上升流体的甲烷含量$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$达到最大1.0时,整个稳定带都充满水合物的时间跨度最小。这显然很容易理解,来自深部的上升流体中携带更多的甲烷,也就是甲烷的输入增大,很大程度上由于甲烷含量较大,扩散的作用明显,甲烷主要靠扩散向上传递,在其他条件不改变的情况下,水合物形成的时间当然缩小。由图 1-G可见上升流体甲烷含量参数$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$越小,形成的水合物体积越大,水合物的体积随着$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$增大而减小,在$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$取值0.6到0.8之间时变化不大,当$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$由0.8增大到1.0时,模拟稳定带底部生成的水合物体积却减小。即当深部上升流体甲烷含量增大时生成的水合物体积却变小,这并不矛盾。因为底部上升流体携带的甲烷含量增大,稳定带内形成水合物的时间跨度必然减小(图 1-H),而且很大程度上,由于甲烷含量较大,扩散的作用明显,甲烷主要靠扩散向上传递,在很短的时间便会使得水合物层快速从稳定带上部延伸至稳定带的底部。即携带高含量甲烷的对流的作用还未起到作用,水合物已经在稳定带底部形成了,正如这时的溶解甲烷量与溶解度曲线的比较所示(图 1-F),所以水合物的体积有所减小。当$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 0.5$时,模拟时间超过单位时间${\widetilde t_0} \approx 6.4{\rm{Ma}}$,仍没有水合物开始形成。即此时甲烷通量太小,无法形成水合物。
3. 模型应用
水合物脊(Hydrate Ridge)为美国俄勒冈外海主动大陆边缘的增生楔。ODP146航次、ODP204航次、IODP(综合大洋钻探计划)311航次在该区开展了大量天然气水合物钻探研究。布莱克海台(Blake Ridge)位于北美东南部的被动大陆边缘,是天然气水合物调查研究程度最高的地区之一。研究表明两地均存在大量水合物[3, 5, 18, 19],且两地均被认为除了部分微生物成因的甲烷,主要源自深部的流体提供了甲烷[6, 17, 20, 21]。许多有关海底沉积中水合物聚集方面的数值模拟工作均对这两处典型的水合物区域进行了研究对比[9, 11, 12, 19, 22, 23]。本文亦选择布莱克海台和水合物脊进行模拟比较,以检验模型的合理性与普适性。
图 2显示了以水合物脊ODP889站位和布莱克海台ODP997站位为背景的模拟结果,所用参数见表 1。
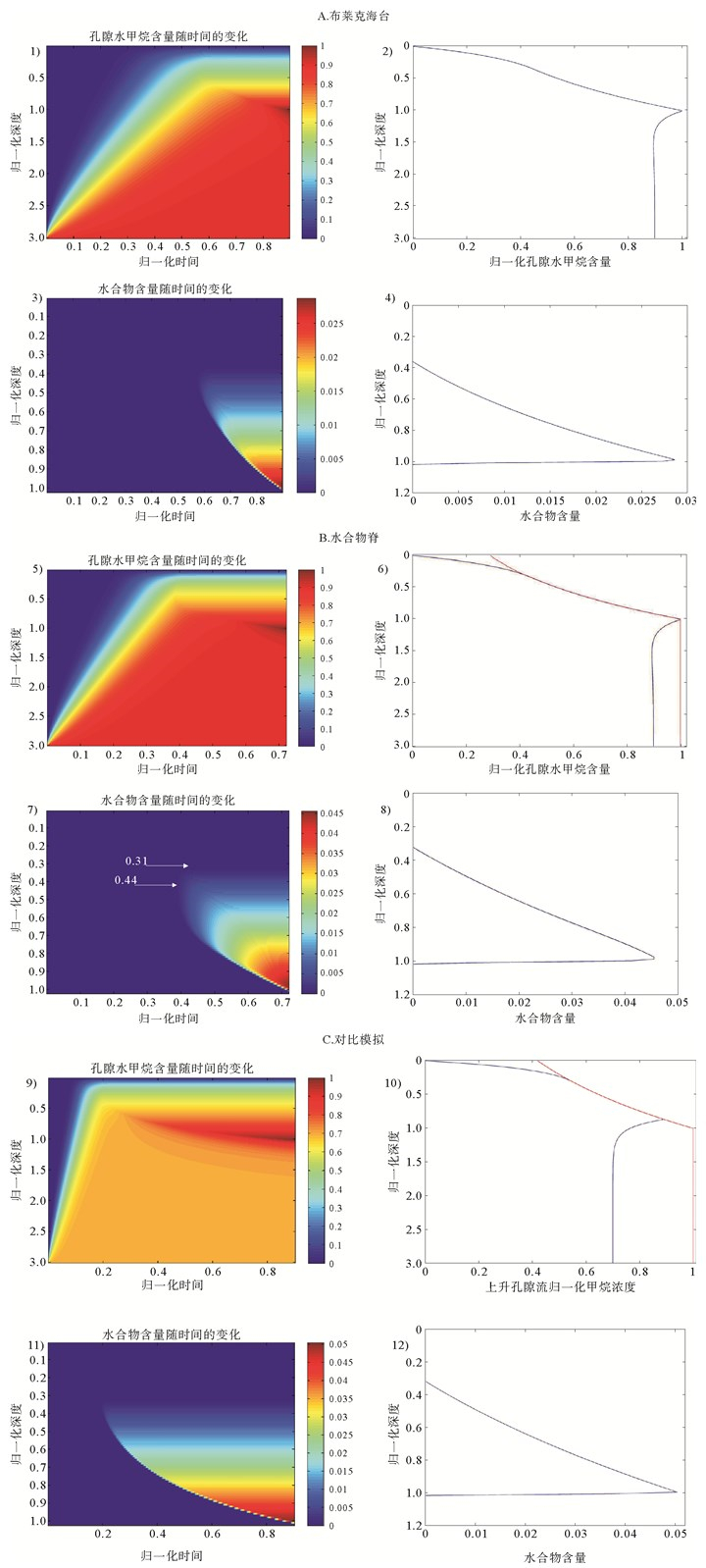
![]() 图 2 海底沉积物中孔隙水溶解甲烷及水合物形成聚集过程模拟A.布莱克海台; B.水合物脊; C.对比模拟(所用参数$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 0.7$, Pe1=0.06, Pe2=-5)。1)、5)、9),孔隙流体溶解甲烷含量随时间变化情况。2)、6)、10), 稳定带底部形成水合物时孔隙水甲烷含量与溶解度的对比。3)、7)、11), 水合物含量随时间变化情况。4)、8)、12), 稳定带底部形成水合物时水合物体积垂直分布Figure 2. Simulation on accumulation of dissolved methane and GH evolution in pore water of submarine sediment表 1 布莱克海台与水合物脊水合物形成过程数值模拟参数Table 1. Parameters for simulation from Blake Platform and Hydrate Ridge
图 2 海底沉积物中孔隙水溶解甲烷及水合物形成聚集过程模拟A.布莱克海台; B.水合物脊; C.对比模拟(所用参数$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 0.7$, Pe1=0.06, Pe2=-5)。1)、5)、9),孔隙流体溶解甲烷含量随时间变化情况。2)、6)、10), 稳定带底部形成水合物时孔隙水甲烷含量与溶解度的对比。3)、7)、11), 水合物含量随时间变化情况。4)、8)、12), 稳定带底部形成水合物时水合物体积垂直分布Figure 2. Simulation on accumulation of dissolved methane and GH evolution in pore water of submarine sediment表 1 布莱克海台与水合物脊水合物形成过程数值模拟参数Table 1. Parameters for simulation from Blake Platform and Hydrate Ridge模型参数 布莱克海台 水合物脊 海底深度z/m 2781[1] 1311[20] 海底温度T/℃ 3.4[1] 2.7[20] 地温梯度G/℃·m-1 0.04[1] 0.054[20] 稳定带厚度Lz/m 450[3] 225[20] 沉积速度Vs/cm·ka-1 22[24] 25[20] 甲烷扩散系数Dm/m2·s-1 10-9[11] 10-9[11] 深部上升流体速度Vl,ext/mm·a-1 -0.26[20] -1[17] 沉积引起的孔隙流体通量Ul,sed/m·s-1 2.32×10-13 2.64×10-13 孔隙流体净通量Ul/m·s-1 -5.82×10-12 -2.22×10-11 Pe1 0.1 0.06 Pe2 -2.57 -5.16 $\widetilde C_{m, ext}^{_{_{\rm{l}}}}$ 0.9 0.9 本文模拟了主动大陆边缘水合物脊和被动大陆边缘布莱克海台两个不同构造环境水合物形成的过程。稳定带底部最大水合物含量在水合物脊可达到沉积孔隙体积的5%(图 2-B),与Davie和Buffett[24]在同样参数条件下模拟的结果一致,与测量孔隙水氯离子浓度得出的水合物垂直分布趋势一致,岩心温度测量估计的最大水合物饱和度3%也在这一范围[25]。在布莱克海台最大水合物的饱和度约3%(图 2-A),这一结果与前人的模拟结果[11-12]相吻合,并与孔隙水离子浓度计算结果[1]一致。这也说明了本文模型的合理性。另一方面也说明了生物成因的甲烷源一般量比较少。
4. 水合物形成和聚集过程
已有模拟[11-12]只是对水合物形成达到最后稳定状态的情形给出描述,本文的模拟形象地给出水合物形成过程的描述。下面给出一般模拟和具体的分析,其中以海底水深2 700 m,海底温度3.4 ℃和地温梯度0.04 ℃/m[1]作为基本的海底沉积环境参数。
水合物首先在稳定带内上部某一位置出现,之后由于沉积的作用水合物层不断增厚,向下延伸直至稳定带的底部形成水合物。从开始形成水合物至其体积不再变化的时间跨度每一个点位都不同,从水合物稳定带顶端到底部需要的时间逐渐增大(图 2)。这主要是由于甲烷溶解度从水合物稳定带底部到海底逐渐减小的缘故。深度越大甲烷的溶解度越大,则沉积作用需要更长的时间才能从上面带来足够的水合物可以使得甲烷的量超过局部溶解度形成水合物。水合物初始形成时其体积比其上部的水合物体积要小的多,此后在孔隙流体对流扩散向上输入溶解甲烷以及沉积从上部输入水合物形式的甲烷的双重作用下,水合物体积增长,直到孔隙流体以对流扩散方式向上输入的甲烷(溶解形式)与沉积作用输出的甲烷(水合物形式)作用抵消,而水合物的体积保持不变。
如图 2-7所示,水合物首先在0.44单位深度$\widetilde z$开始析出,而模拟稳定时水合物上限位置向上迁移了0.13单位深度$\widetilde z$至0.31单位深度$\widetilde z$,即水合物层向上延伸了约58 m(以水合物稳定带厚度450 m计算)。这是由于水合物形成初期在接近海底的区域,甲烷以扩散的作用向上传输,使得这里的甲烷量最先达到局部的溶解度。随着时间的推移,对流作用传输甲烷逐渐成为主导方式,使得达到溶解度的区域向上迁移,水合物出现区域也就相应地向海底有限地扩张。
当上升孔隙流体速度较大时,如Pe2=-8时,由于甲烷在孔隙流体中的高含量以及孔隙流体的高速度,此时才仅用约1/4的单位时间${\widetilde t_0}$(图 1-D)稳定带底部便形成了水合物。如此短的时间内,甲烷含量为$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$的深部上升流体还未到达稳定带底部(图 1-E)。整个稳定带内形成水合物需要的甲烷均以溶解甲烷的扩散方式提供,因此形成水合物的体积有所减小。当底部上升流体携带的甲烷含量较大时,稳定带内形成水合物的时间跨度必然减小(图 1-H),而且很大程度上,由于甲烷含量较大,扩散的作用明显,甲烷主要靠扩散向上传递,在很短的时间便会使得水合物层快速从稳定带上部延伸至稳定带的底部。即携带高含量甲烷的对流的作用还未起到作用,水合物已经在稳定带底部形成了,正如这时的溶解度曲线所示(图 1-F),因此水合物的体积有所减小。其他参数相同,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$由0.9减小至0.7,稳定带底部形成水合物的时间跨度却由0.723 2单位时间$\widetilde t$增加至2.257 5倍单位时间$\widetilde t$ (图 2-B、C,${\widetilde t_0} = 1.6053{\rm{Ma}}$)。可见深部上升流体甲烷含量对水合物演化时间尺度的重要影响。
水合物在甲烷含量大于局部孔隙水溶解度时开始形成,之后溶解于孔隙水中的甲烷浓度保持不变。在整个沉积剖面中甲烷随着时间的推移有着几个不同的相带。模拟初始阶段,整个稳定带内水合物还没有形成,甲烷溶解于孔隙水中。首先在稳定带内的上部某一位置最先开始出现甲烷的量超越其局部溶解度,自此之后,这一位置以上至海底,甲烷基本都是以溶解形式存在。而这一位置以下,甲烷则以溶解形式和固态水合物形式共存于沉积孔隙中。除了稳定带顶部甲烷的浓度小于溶解度以液相的形式存在,大部分稳定带内甲烷小部分以溶解的形式存在于孔隙水中,大部分都转变为了固态水合物形式存在。
甲烷溶解度随深度的变化也控制了甲烷的对流和扩散通量,对水合物系统甲烷的供给和排出具有重要的影响。在水合物形成初期,正是由于甲烷溶解度自水合物稳定带底部向海底逐渐减小,因此在海底剖面每一空间点,来自深部以对流和扩散方式供给的甲烷大于这一点向上对流和扩散方式输出的甲烷量。而由于沉积的作用,从这一点向下输出水合物形式的甲烷又大于来自上部供应的水合物形式的甲烷。因此对流扩散方式和连续沉积双重作用引起了水合物的生长。当对流和扩散方式向上输入的甲烷量与沉积作用输出的甲烷量达到平衡时,水合物的体积就不再改变(图 2)。总之,海底深部甲烷向上的传输,少部分以对流扩散的形式从海底进入大海,大部分以固态水合物的形式留在了水合物稳定带内。其中甲烷在海底沉积孔隙流体中的溶解度的变化趋势(水合物稳定带底部甲烷溶解度最大,而向海底逐渐减小)使得来自深部的甲烷在向海底的传输过程中,大部分的甲烷就像固体颗粒经过筛子一样被过滤了。而这一甲烷溶解度变化曲线恰与水合物稳定域重合,在这双重作用下便形成了水合物,只有少部分溶解甲烷以对流和扩散的方式穿过海底进入水体中。
而有关水合物的成藏机理方面,水合物再循环机制(hydrate recycling mechanism)[26-29]可能只是发生在沉积速率较大和构造活动较强的地区。最近提出的甲烷溶解度变化机制(solubility-curvature mechanism)[11]更代表了较普遍的海底水合物及其下伏游离甲烷气形成情况。本文模拟表明了甲烷溶解度曲线对水合物形成、体积和分布[11]的重要影响(图 2),但溶解度只是水合物形成的一个背景,深部上升流体甲烷含量、上升流体的通量决定了整个水合物系统甲烷量的输入和输出。因此,建议深部上升流体甲烷含量、上升流体的通量以及水深、地热梯度为海底天然气水合物形成和聚集的主要控制因素。
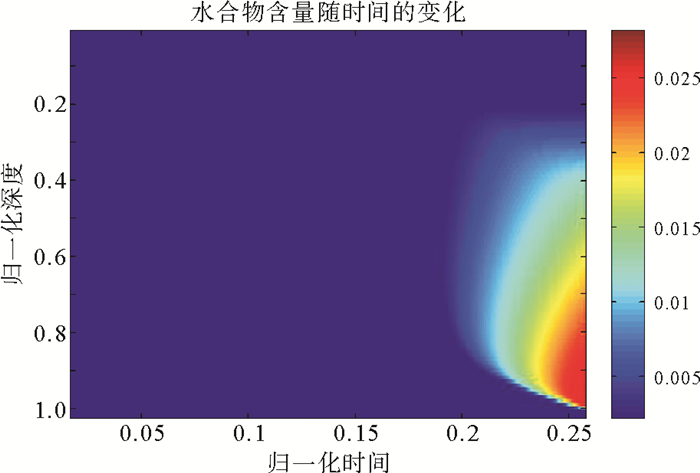
而当深部上升流体供给的甲烷量比较充足时,水合物形成过程显示不稳定的特点(图 3)。
5. 结论
本文建立的模型预测了深部甲烷流体向上传输的情况下水合物在时间和空间尺度上的形成和聚集过程。通过3个无量纲参数即Pe1、Pe2及$\widetilde C_{m, ext}^{_{_{\rm{l}}}}$(分别代表沉积压实引起的孔隙流体对流与扩散的比率、深部流体向上对流传输与扩散的比率、深部上升流体的甲烷含量)形象地给出了水合物形成过程的描述。水合物首先在稳定带内上部某一位置形成,随后由于沉积作用向下延伸而在稳定带的底部形成水合物。水合物演化时间随着参数Pe1、Pe2及$\widetilde C_{m, ext}^{_{_{\rm{l}}}}$的增大而减小;水合物含量随着参数Pe1、$\widetilde C_{m, ext}^{_{_{\rm{l}}}}$的增大而减小,而随着Pe2的增大而增大。甲烷溶解度曲线对水合物形成、体积和分布有重要的影响,但深部上升流体甲烷含量、上升流体的通量决定了整个水合物系统的甲烷量输入和输出。因此,水深、地温梯度、深部上升流体甲烷含量、上升流体通量4个参数是海底天然气水合物形成的主要控制因素。
-
图 1 模型参数敏感度分析
A.水合物含量Sh与Pe1(表征海底沉积的快慢)的关系(Pe2=-2.6,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$, 以最小/最大沉积速率为10/100 cm/ka得出Pe1介于0.05和0.3之间);B.水合物演化时间t与Pe1的关系(Pe2=-2.6,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$);C.水合物含量Sh与Pe2的关系(Pe1=0.1, $\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$);D.水合物演化时间t与Pe2的关系(Pe1=1.0,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$);E.稳定带底部形成水合物时海底沉积中的溶解甲烷量(红色线)与溶解度(蓝色线)的比较(Pe1=1.0,Pe2=-8,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1.0$);F.稳定带底部形成水合物时海底沉积中的溶解甲烷量(红色线)与溶解度(蓝色线)的比较(Pe1=1.0,Pe2=-2.6,$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1.0$);G.水合物含量Sh与$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$的关系($\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$代表深部上升流体的甲烷含量, Pe1=1.0,Pe2=-2.6);H.水合物演化时间t与$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 1$的关系(Pe1=1.0,Pe2=-2.6)
Figure 1. Model sensitivity to parameters
图 2 海底沉积物中孔隙水溶解甲烷及水合物形成聚集过程模拟
A.布莱克海台; B.水合物脊; C.对比模拟(所用参数$\widetilde C_{m, ext}^{_{_{\rm{l}}}} = 0.7$, Pe1=0.06, Pe2=-5)。1)、5)、9),孔隙流体溶解甲烷含量随时间变化情况。2)、6)、10), 稳定带底部形成水合物时孔隙水甲烷含量与溶解度的对比。3)、7)、11), 水合物含量随时间变化情况。4)、8)、12), 稳定带底部形成水合物时水合物体积垂直分布
Figure 2. Simulation on accumulation of dissolved methane and GH evolution in pore water of submarine sediment
表 1 布莱克海台与水合物脊水合物形成过程数值模拟参数
Table 1 Parameters for simulation from Blake Platform and Hydrate Ridge
模型参数 布莱克海台 水合物脊 海底深度z/m 2781[1] 1311[20] 海底温度T/℃ 3.4[1] 2.7[20] 地温梯度G/℃·m-1 0.04[1] 0.054[20] 稳定带厚度Lz/m 450[3] 225[20] 沉积速度Vs/cm·ka-1 22[24] 25[20] 甲烷扩散系数Dm/m2·s-1 10-9[11] 10-9[11] 深部上升流体速度Vl,ext/mm·a-1 -0.26[20] -1[17] 沉积引起的孔隙流体通量Ul,sed/m·s-1 2.32×10-13 2.64×10-13 孔隙流体净通量Ul/m·s-1 -5.82×10-12 -2.22×10-11 Pe1 0.1 0.06 Pe2 -2.57 -5.16 $\widetilde C_{m, ext}^{_{_{\rm{l}}}}$ 0.9 0.9 -
[1] Paull C K, Matsumoto R, Wallace P J. Proceedings of the ocean drilling program, initial reports[R]. College Station, TX (Ocean Drilling Program), 1996, 164.
[2] 吴能友, 梁金强, 王宏斌, 等.海洋天然气水合物成藏系统研究进展[J].现代地质, 2008, 22(3): 356-362. http://d.old.wanfangdata.com.cn/Periodical/xddz200803003 WU Nengyou, LIANG Jinqiang, WANG Hongbin, et al. Marine gas hydrate system: state of the art (in Chinese) [J]. Geoscience, 2008, 22(13): 356-362. http://d.old.wanfangdata.com.cn/Periodical/xddz200803003
[3] Paull C K, Matsumoto R. Proceedings of the ocean drilling program, scientific results [R].College Station, TX (Ocean Drilling Program), 2000, 164: 3-10.
[4] Dickens G R. Rethinking the global carbon cycle with a large, dynamic and microbially mediated gas hydrate capacitor [J]. Earth and Planetary Science Letters, 2003, 213: 169-183. doi: 10.1016/S0012-821X(03)00325-X
[5] Tréhu A M, Long P E, Torres M E, et al. Three-dimensional distribution of gas hydrate beneath southern Hydrate Ridge: constraints from ODP Leg 204 [J]. Earth and Planetary Science Letters, 2004, 222: 845-862. doi: 10.1016/j.epsl.2004.03.035
[6] Hyndman R D, Davis E E. A mechanism for the formation of methane hydrate and seafloor bottom-simulating reflectors by vertical fluid expulsion [J]. Journal of Geophysical Research, 1992, 97(B5): 7025-7041. doi: 10.1029/91JB03061
[7] Rempel A W, Buffett B A. Formation and accumulation of gas hydrate in porous media [J]. Journal of Geophysical Research, 1997, 102(B5): 10151-10164. doi: 10.1029/97JB00392
[8] Rempel A W, Buffett B A. Mathematical models of gas hydrate accumulation [J]. Geological Society, London, Special Publications, 1998, 137(1): 63-74. doi: 10.1144/GSL.SP.1998.137.01.05
[9] Xu W Y, Ruppel C. Predicting the occurrence, distribution, and evolution of methane gas hydrate in porous marine sediments [J]. Journal of Geophysical Research-Solid Earth, 1999, 104(B3): 5081-5095. doi: 10.1029/1998JB900092
[10] Zatsepina O Y, Buffett B A. Thermodynamic conditions for the study of gas hydrates in the seafloor [J]. Journal of Geophysical Research, 1998, 103(B10): 24127-24139. doi: 10.1029/98JB02137
[11] Davie M K, Buffett B A. A numerical model for the formation of gas hydrate below the seafloor [J]. Journal of Geophysical Research-Solid Earth, 2001, 106(B1): 497-514. doi: 10.1029/2000JB900363
[12] Bhatnagar G, Chapman W G., Dickens G R, et al. Generalization of gas hydrate distribution and saturation in marine sediments by scaling of thermodynamic and transport processes [J]. American Journal of Science, 2007, 307: 861-900. doi: 10.2475/06.2007.01
[13] Haacke R R, Westbrook G K, Riley M S. Controls on the formation and stability of gas hydrate-related bottom-simulating reflectors (BSRs): A case study from the west Svalbard continental slope [J]. Journal of Geophysical Research, 2008, 113: B05104. http://cn.bing.com/academic/profile?id=2bf54aea3b4b5906f0345fbc097e4157&encoded=0&v=paper_preview&mkt=zh-cn
[14] Haacke R R, Westbrook G K, Hyndman R D. Gas hydrate, fluid flow and free gas: Formation of the bottom-simulating reflector [J]. Earth and Planetary Science Letters, 2007, 261(3-4): 407-420. doi: 10.1016/j.epsl.2007.07.008
[15] Egeberg P K, Dickens G R. Thermodynamic and pore water halogen constraints on hydrate distribution at ODP Site 997 (Blake Ridge) [J]. Chemical Geology, 1999, 153: 53-79. doi: 10.1016/S0009-2541(98)00152-1
[16] Davie M K, Zatsepina O Y, Buffett B A. Methane solubility in marine hydrate environments [J]. Marine Geology, 2004, 203(1-2): 177-184. doi: 10.1016/S0025-3227(03)00331-1
[17] Wang K, Hyndman R D, Davis E E. Thermal effects of sediment thickening and fluid expulsion in accretionary prisms-model and parameter analysis [J]. Journal of Geophysical Research, 1993, 98(6): 9975-9984. http://cn.bing.com/academic/profile?id=60c84627fccb80e80f2d07e8972cdc3b&encoded=0&v=paper_preview&mkt=zh-cn
[18] Dickens G R, Paull C K, Wallace P. Direct measurement of in situ methane quantities in a large gas-hydrate reservoir [J]. Nature, 1997, 385(6615): 426-428. doi: 10.1038/385426a0
[19] Torres M E, Wallman, K, Trehu A M, et al. Gas hydrate growth, methane transport, and chloride enrichment at the southern summit of Hydrate Ridge, Cascadia margin off Oregon [J]. Earth and Planetary Science Letters, 2004, 226: 225-241. doi: 10.1016/j.epsl.2004.07.029
[20] Haeckel M, Suess E, Wallman K, et al. Rising methane gas bubbles form massive hydrate layers at the seafloor [J]. Geochimica et Cosmochimica Acta, 2004, 68: 4335-4345. doi: 10.1016/j.gca.2004.01.018
[21] Wallmann K, Aloisi G, Obzhirov A, et al. Kinetics of organic matter degradation, microbial methane generation, and gas hydrate formation in anoxic marine sediments [J]. Geochimica et Cosmochimica Acta, 2006, 70(15): 3905-3927. doi: 10.1016/j.gca.2006.06.003
[22] Westbrook G K, Carson B, Musgrave R J, et al. Proceedings of the ocean drilling program, initial reports [R].College Station, TX (Ocean Drilling Program), 1994, 146. http://www-odp.tamu.edu/publications/146_1_IR/VOLUME/CHAPTERS/146irpt1.pdf
[23] Borowski W S, Paull C K, Ussler Ⅲ W. Marine pore-water sulfate profiles indicate in situ methane flux from underlying gas hydrate [J]. Geology, 1996, 24(7): 655-658. doi: 10.1130/0091-7613(1996)024<0655:MPWSPI>2.3.CO;2
[24] Davie M K, Buffett B A. A steady state model for marine hydrate formation: Constraints on methane supply from pore water sulfate profiles [J]. Journal of Geophysical Research-Solid Earth, 2003, 108(B10): 2495. http://cn.bing.com/academic/profile?id=7bbd3b4c84bfe1244db235a94e4789dd&encoded=0&v=paper_preview&mkt=zh-cn
[25] Kastner M, Kvenvolden K A, Whiticar M J, et al. Relation Between Pore Fluid Chemistry and Gas Hydrates Associated with Bottom-Simulating Reflectors at the Cascadia Margin, Sites 889 and 892 [C]//In: Carson B, Westbrook G K, Musgrave R J, Suess E, Eds. Proceedings of the Ocean Drilling Program, Scientific Results, 1995, 146: 175-187.
[26] Kvenvolden K A. Gas hydrates-geological perspective and global change [J]. Reviews of Geophysics, 1993, 31(2): 173-187. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=756561cd96b062bf9ab8a8aaf8aba11d
[27] Paull C K, Ussler W I, Borowski W S. Natural gas hydrates, chapter sources of biogenic methane to form marine gas hydrates [J]. Annals of the New York Academy of Sciences, 1994, 715: 392-409. doi: 10.1111/j.1749-6632.1994.tb38852.x
[28] Pecher I A, Minshull T A, Singh S C, et al. Velocity structure of a bottom simulating reflector offshore Peru: Results from full waveform inversion [J]. Earth and Planetary Science Letters, 1996, 139(3-4): 459-469. doi: 10.1016/0012-821X(95)00242-5
[29] Huene R V, Pecher I A. Vertical tectonics and the origins of BSRs along the Peru margin [J]. Earth and Planetary Science Letters, 1999, 166(1-2): 47-55. doi: 10.1016/S0012-821X(98)00274-X
-
期刊类型引用(4)
1. 秦雨珂,程珂珂,杨波,郑惠娜,蔡中华,肖宝华,周进. 珊瑚共生体碳代谢特征研究进展. 生态学报. 2024(09): 3561-3574 .  百度学术
百度学术
2. 陈雨梅,齐钊,尹连政,常逢彤,鞠涵烨,刁晓平. 不同珊瑚对酸化、苯并[a]芘单一和复合胁迫的生理响应. 生态毒理学报. 2023(03): 456-464 .  百度学术
百度学术
3. 胡子恒. 海水酸化和升温对三角褐指藻光合和呼吸的影响. 生物化工. 2023(06): 125-128 .  百度学术
百度学术
4. 陈柳云,吴苑,张玉强. MEBM视角下的广东徐闻珊瑚礁保护研究进展. 生态科学. 2022(04): 231-241 .  百度学术
百度学术
其他类型引用(8)



 下载:
下载: