Simulation of submarine slope stability related to hydrate dissociation
-
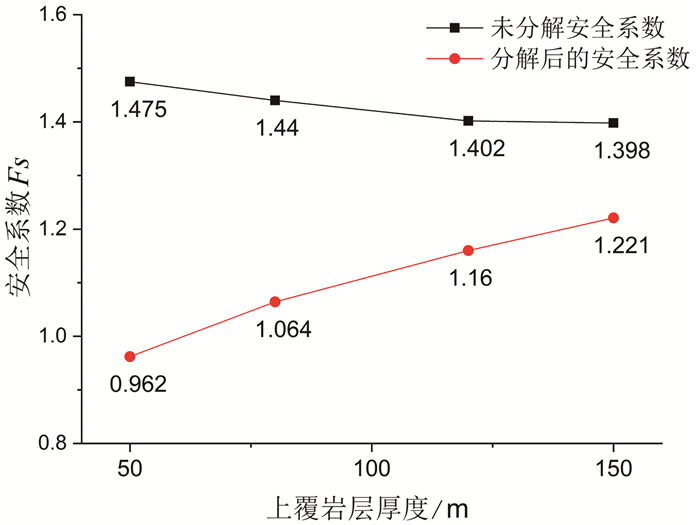
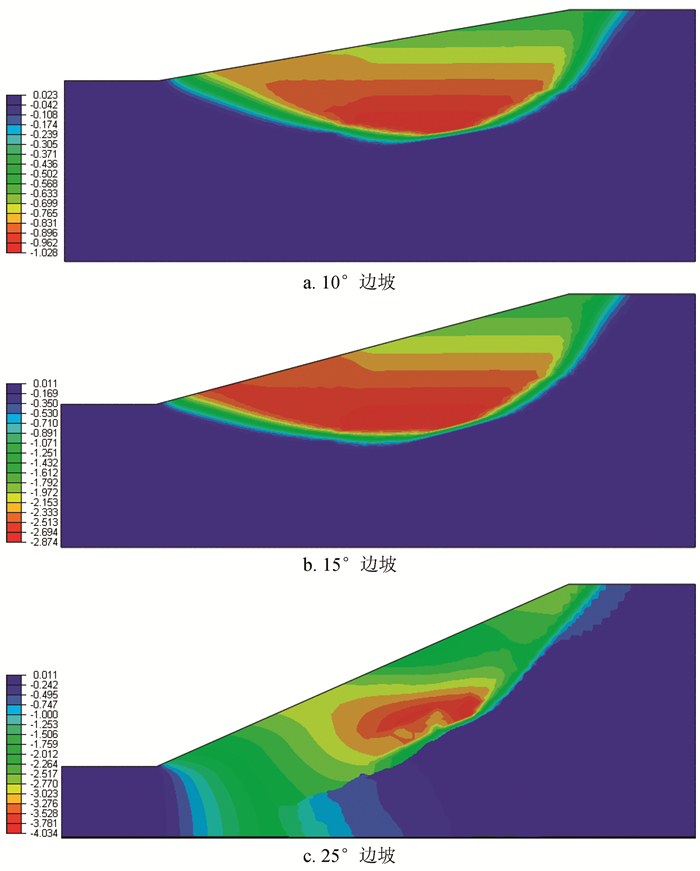
摘要: 海底边坡失稳会给人类造成巨大危害，部分海底边坡失稳案例被证实与水合物分解有关。由于海底条件的复杂性，人们很难直接观察水合物分解引起的海底边坡失稳过程。数值模拟可以相对准确地预测水合物分解可能引起的海底边坡失稳状况。通过选用基于ABAQUS软件的有限元强度折减法，模拟海底边坡失稳的过程并得到相应结果，分析了水合物分解程度、水合物带上覆厚度、边坡角度等因素对海底边坡稳定性的影响。结果表明，正常情况下，塑性区首先在坡脚区域出现并逐渐向上发展至坡顶；当水合物分解达到一定程度后，塑性区首先出现在水合物带，随后自水合物带向上发展至坡顶，并和随后在坡脚出现的塑性区形成贯通边坡的塑性带。水合物埋藏越深，越有可能造成大规模的滑坡；边坡角度高于15°时，水合物分解会急剧促进边坡失稳。Abstract: Hydrate dissociation is a significant factor causing submarine slope slide, which is dangerous to human operation. Due to the complex condition of seabed, it is hard to observe the process of slope slide directly. Numerical simulation is an effective approach to acquire some important parameters such as the slide area, slide scale, sliding distance and safety factors etc. Choosing shear strength reduction technique of the finite element based on the software of ABAQUS, we could not only simulate both the process and result of a slope slide, but also evaluate the influence of hydrate dissociation. By changing the parameters of modeling, the characteristics of seafloor can be considered. Of course, the inducing factor is the interaction between the structure of slope and hydrate dissociation. It can guide the hydrate exploitation process and avoid some possible problems by integration of the theoretical and simulation results.
-
天然气水合物是由水与天然气在高压低温条件下形成的结晶物质[1]，直观上与冰相似，广泛分布于海洋深水地层和高纬度极地冻土地层中[2]。目前普遍认为水合物中所储存的能量是所有传统化石能源的2倍[3]。同时由于其能量密度大、污染程度低等因素[4]，被认为是石油等传统化石能源的接替能源。目前水合物开发方向的研究主要包含3个方面：水合物成藏机理，水合物勘探开采以及相关地质问题研究。人们进行大量的水合物开采室内实验和数值模拟研究之后(例如Kurihara采用MH21-HYDRES[5]，White和McGrail采用STOMP-HYD[6]，Moridis采用TOUGH + HYDRATE[7, 8]等)，水合物分解所引起的地质问题开始逐渐得到各界的重视。研究认为，水合物开采分解所致的海底地质风险不仅会作用在开采范围，同时会诱发长期的巨大的地质灾害及环境风险，海底滑坡是其典型表现形式[9, 10]。目前关于水合物分解对海底边坡稳定性影响的科学研究尚处于理论探索阶段。
水合物分解会严重降低沉积层的强度[11, 12]，具体表现在以下2点：(1)水合物分解后其自身在水合物沉积层中的胶结、支撑作用的消失，其分布区域的力学强度大大降低；(2)注热开采或地层流动性较差的情况下，水合物分解产生的大量气体不能及时从地层中排出，会在孔隙内部形成异常高压，进而破坏储层结构，降低储层强度及承载能力。两方面作用使得储集层强度严重降低，进而引起地质失稳问题[13]。Sultana研究认为已知规模最大的海底滑坡Storgga滑坡的主要诱因是水合物分解，同时采用Comsol软件进行的水合物分解多场耦合的数值分析，进一步证实了水合物分解会引起大规模的海底滑坡[14]。Gupta等采用C++编程建立了系统的耦合热、化学、静水压力、岩石力学行为的水合物分解模型，论证了岩石力学行为在水合物分解过程中的重要性，并且结合数值模拟和实验得出结论：水合物分解会导致海底地层出现大于5%的体积应变[15]。Li等采用Flac3D建立了含水合物的海底边坡模型，论证水合物分解对海底边坡失稳的影响的同时分析了水合物分解时边坡各个位置向下运动的位移[16]。周丹分析认为海底滑坡规模远大于陆地滑坡且当边坡角度小于10°时，由于内部水合物层强度降低，仍有可能发生海底滑坡[17]。杨晓云等进一步探讨了水合物分解对海底沉积层岩石力学参数的影响机理及影响程度，并认为胶结强度的降低是海底边坡失稳的主导因素[18]。马云[19]、于桂林[20]、张振飞[21]分别采用ABAQUS软件建立了一系列含水合物边坡的数值模型，并评估了边坡稳定性和失稳范围及潜在的影响因素。
上述研究存在以下几方面的不足之处：(1)没有考虑水合物实际开采过程，采取单一水合物饱和度进行分析。水合物分解开采过程中，水合物自钻孔向两侧逐渐分解，即沿井眼径向上水合物饱和度不均匀；(2)本构模型及材料参数论证不足。不同水合物饱和度下沉积层强度参数直接影响整个边坡的力学行为，系统详实本构方程描述在相关分析中至关重要；(3)人工迭代试算的计算方法。上述诸多分析均采用人工计算的方式，使得所得结果不连续、非动态，且计算过程繁琐。本文在前人研究的基础上，采用基于ABAQUS的强度折减法，结合实际开采情况，选取连续的水合物沉积层本构模型，实现自动迭代折减计算，分析了开采过程中不同边坡角度、埋藏深度条件下水合物分解程度对边坡稳定性的影响情况。研究结果表明，水合物分解是边坡失稳的主导因素，在20°边坡条件下，井眼附近水合物地层强度低于沉积层强度时，会引起较大规模的海底滑坡；边坡角度和水合物分解程度共同作用下边坡会急剧失稳。同时，水合物带的位置及分解程度决定了边坡的稳定性及滑坡的规模。
1. 模型建立
1.1 水合物本构模型
水合物沉积层的本构模型建立是水合物分析中的重点难点部分。其具体表现为水合物对沉积层特有的3个作用:一是水合物对沉积物的胶结作用；二是水合物分解对沉积层结构的破坏；三是由于水合物强度高于单一沉积砂泥岩强度，使得含水合物的沉积层强度(在水合物未分解或轻度分解条件下)普遍高于不含水合物层[13, 22]。大量分析认为，影响水合物在地层中岩石力学行为特征的主要因素同样可以概括为3类：岩土粒径分布和岩性分布[23, 24]；水合物成藏原因[25-27]；水合物饱和度分布[28]。因此，本构模型的建立势必要引入水合物饱和度[29]。目前人们对水合物本构模型进行了大量的三轴实验并得到了一系列具有一定可信度的水合物沉积层本构模型[30]。其中应用较多的分别是基于摩尔—库伦模型和剑桥模型改进建立的水合物沉积层本构模型[31, 32]。综合分析各种已有模型，本文所选取的本构模型是基于非线性理论和摩尔—库伦模型所建立的，以水合物饱和度为基础变量，建模时离散沉积层和水合物层，并最终得到综合的抗剪强度参数及杨氏模量。该模型不仅可以较好地描述不同区块动态水合物饱和度下的沉积层应力应变关系[33]，同样与Miyazaki等进行的大量关于水合物的三轴实验结果相吻合，因此, 以该模型作为水合物沉积层力学特征的本构模型[34]。关系式如下所示[32]：
$$ c = {c_s} + {c_h} = {c_1}\left( {1 - {e^{ - \frac{{\sigma _3^\prime }}{{\sigma _t^\prime }}}}} \right) + {c_2}s_h^{{c_s}} $$ $$ \begin{array}{l}{\sin \varphi=\sin \varphi_{s}+\sin \varphi_{h}=} \\ {\sin \left[\delta_{1}-\delta_{2} \ln \left(\frac{\sigma^{\prime}_{3}}{1_{M P a}}\right)\right]+\delta_{3} s_{h}\left(1-e^{-\frac{\gamma}{\delta_{4}}}\right)}\end{array} $$ $$E=E_{s}+E_{h}=e_{1}\left(\frac{\sigma_{3}^{\prime}}{1_{M P a}}\right)^{\theta_{2}}+e_{3} s_{h} $$ 式中，c、cs、ch分别是水合物沉积层、砂和水合物的内聚力(kPa)；φ、φs、φh分别是水合物沉积层、砂和水合物的摩擦角(°)；E、Es、Eh分别是水合物沉积层、砂和水合物的弹性模量(kPa); sh是水合物饱和度。其他参数在具体某一区块为常数，σ′3为有效围压(kPa)；γ是内部剪切应变；δ1和δ2是与相对密度和固体材料相关的常数，δ3是与水合物的存在而引起的膨胀增加相关的常数，δ4是与脱粘/断裂相关的剪切应变相关的常数。c1、c2分别为所测沉积层与水合物的粘聚力(kPa)；c3为拟合所得的指数参数；e1、e2、e3是Pinkert等建立模型时拟合得出的常数。确定岩土强度的方法包括室内实验和现场原位测试两大类方法[2]，结合我国南海神狐海域水合物沉积层骨架强度，具体参数如表 1所示。
物理量 数值 单位 c1 293 kPa c2 1960 kPa c3 1.7 σ′3 1962 kPa σ′t 382 kPa δ1 0.4 δ2 0.2 δ3 0.22 δ4 0.04 e 2.72 e1 548000 kPa e2 265800 kPa e3 450000 kPa γ 1.2 基于ABAQUS的有限元强度折减法
传统的边坡稳定性分析方法主要包括极限分析、极限平衡和以有限元为主的数值计算方法[36]。随着计算机技术和有限元的发展，基于应力场的稳定分析方法和有限元强度折减法越来越得到普遍认可，并逐渐成为未来边坡稳定性分析的发展方向。陆上边坡稳定性分析方法同样适用于海底边坡稳定性分析[37, 38]。本文即采取有限元强度折减法作为水合物分解导致的边坡稳定性分析的指导方法。强度折减法由Zienkiewicz于1975年提出[39]，该方法的核心是抗剪强度折减系数，其定义为：在外载荷保持不变的情况下，边坡内土体所提供的最大抗剪强度与外载荷在边坡内产生的实际剪应力之比。临界破坏时的强度折减系数Fr即为边坡的安全系数Fs。
折减后的抗剪强度参数可分别表达为[40]：
$$ \begin{aligned} c_{m} &=c / F_{r} \\ \varphi_{m} &=\arctan \left(\tan \varphi / F_{r}\right) \end{aligned} $$ 式中：cm、φm是维持平衡所需要的或土体实际发挥的内聚力和摩擦角；Fr是强度折减系数。
计算中需要假定不同的强度折减系数Fr，使用折减后的强度参数进行有限元分析。在ABAQUS中，将折减系数定义为场变量，进而实现折减系数在计算过程中自动增加，并最终得到计算中止时的折减系数。在此基础上，根据下部分所选取的边坡失稳准则，确定边坡失稳的安全系数，并根据所得的计算结果进行分析。
1.3 边坡失稳准则
边坡失稳的判据同样直接影响对边坡稳定性的认识情况及强度折减法的准确性。目前判断土坡达到临界破坏的评价标准主要有如下3种[38, 40]：①形成连续的塑性贯通区；②边坡顶部拐点发生显著位移；③计算因不收敛而终止。
在实际计算过程中，塑性区一般在边坡底部开始形成，并逐渐向上发展。当塑性区最终发展形成连续的贯通区时，会导致边坡顶部拐点位置产生位移。随着岩土强度进一步折减，边坡顶部特征部位会产生一个严重的拐点，即说明此时边坡发生失稳，产生了较大变形。若再进一步折减岩土强度，就会引起计算的不收敛。即这3种判断依据是存在一个时间上的联系的。同时，根据数值模拟结果，发现这3种判据所确定的安全系数是逐渐增大的，但自塑性贯通区形成至计算中断，此过程折减系数变化范围不超过其数值的5%。
在实际分析过程中，只有以统一评价标准进行对比分析才可以得到可信的结果。而前2种评价标准只能根据计算过程中的云图分布或顶部节点位移变化曲线，人为地选取一折减系数作为安全系数，由于缺乏定量标准，会给不同情况下的对比带来主观误差。第3种判断方式具有统一的评价标准，如只需固定两迭代步之间的最小增量，即可形成统一评价标准。因此，本文以计算终止为边坡失稳的评价标准，以利于在同一标准下评价不同情况下的边坡稳定性问题。
2. 水合物边坡模型
2.1 数值模型建立
本模型模拟由于开发过程中水合物分解引起的水合物带强度特征变化对海底边坡稳定性的影响。随着时间推移，以井眼为中心，水合物带分解程度及分解范围逐渐扩大。通过模拟计算水合物特定分解范围、程度、时间点下边坡的安全系数，评估由水合物分解对边坡稳定性的影响。通过数值模拟塑性区分布云图及位移云图，确定水合物分解引起的边坡失稳规模及程度的变化。
对于理想的三维均质地层，通过基础弹塑性力学理论，可以简化为二维平面模型。对基本模型进行网格划分。为了保证计算精度，网格结构选择结构化的四边形单元，网格属性确定为平面应变网格。模型的基本尺寸如图 1所示。模型水平跨度1000m，总厚度400m，水合物埋深120m，边坡角度20°，坡顶水平跨度200m，1区域对称轴位置为井眼位置，将水合物带以井眼为中心，向两侧划分区域，以模拟不同的分解程度和分解范围[41]。本模型为基本模型，后续模型在本模型基础上进行适当修改。
2.2 边界条件和初始状态
结合典型边坡失稳分析，限制边坡左右边界在水平方向上的位移，限制边坡下部边界在各个方向的位移。同时，结合我国南海神狐海域水合物实际勘探情况，选取合适条件，确定数值模拟所需的基本参数。实际勘探数据与模型采用数据如表 2所示。
Table 2. Exploration data and numerical model selected data for hydrate formations in the Shenhu area参数 神狐海域勘探数据 模型选用数据 水深/m 500~2000 1300~1650 水合物埋深/m 7~350 50~150 海底坡脚/(°) 最高达30 10~25 颗粒密度/(g/cm3) 2.695~2.716 2.700 海水密度/(g/cm3) 1.040 1.040 水合物密度/(g/cm3) 0.980 0.980 水合物饱和度 0.45~0.92 0.8 沉积物孔隙度 0.27~0.63 0.4 整个模型只受来自海水的上覆压力及自身的重力影响[42-44]。采用地应力平衡分析对施加初始载荷的数值模型进行地应力平衡，在地应力平衡状态的基础上进行数值分析模拟。对于不同的水合物分解程度，可以计算出水合物残余饱和度，然后将其代入本构模型，可计算该条件下的强度参数。根据设定方案，计算所得各分解程度下材料强度如表 3所示。
表 3 模型材料强度参数Table 3. Strength parameters of numerical model材料 内聚力
/kPa摩擦角
/(°)杨氏模量
/MPa密度
/(g/cm3)沉积层 291.2 18.6 56.3 2.200 水合物层分解程度 未分解 1562.9 26.0 206.0 1.844 分解30% 504.2 22.7 89.7 1.794 分解60% 308.6 19.4 41.2 1.745 分解80% 89.2 17.3 23.7 1.711 分解100% 35.4 15.2 10.28 1.688 3. 模型计算分析
3.1 水合物分解程度对边坡稳定性影响
在如图 1所示模型上，设计7种不同的计算方案来分析水合物分解范围及程度逐渐扩大的过程。方案设计基本依据为：钻孔引起的水合物分解，随时间推移，水合物分解范围及分解程度不断变大。方案简介如下：作为对比方案，首先对不含天然气水合物层的海底边坡进行稳定性分析；之后对含水合物但未分解的海底边坡进行稳定性分析；随后将1区域水合物分解程度设为30%，其他区域未分解；将1区域分解程度设为60%，2区域分解程度设为30%，其他区域未分解；依次类推，具体计算方案如表 4所示。
表 4 模拟方案设计Table 4. Conceptual design of simulation方案 方案描述 方案1 不含水合物层的均质海底边坡模型 方案2 含水合物且水合物未分解的海底边坡模型 方案3 1区分解30%，其他区域未分解 方案4 1区分解60%，2区分解30%，其他区域未分解 方案5 1区分解80%，2区分解60%，3区分解30%，4区未分解 方案6 1区分解100%，2区分解80%，3区分解60%，4区分解30% 方案7 1、2区分解100%，3、4区分解80% 部分方案数值模拟如图 2所示。前3种方案下塑性区域发展情况基本相同：塑性区域首先出现在坡脚，逐渐发展至坡顶形成塑形贯通区，塑形贯通区及其所包含的区域是滑坡发生的范围。在ABAQUS中可以通过塑性区的位置以及边坡在水平方向上的位移来判断边坡失稳的范围与规模。对比方案1、2、3，说明水合物带的存在不会降低边坡的稳定程度，由于方案3下水合物带的强度是高于沉积层的强度的，因此，可以说明局部的强度增加对边坡整体的稳定性影响不显著。同样，对比方案2、3，可以认为局部强度的小幅度降低对边坡整体的稳定性影响不显著。随着水合物分解程度的增加，自方案4开始出现贯穿水合物带的塑形区，如图 3所示。
![]()
图 2 部分方案计算终止时塑性区分布云图Figure 2. Contours of plastic zone when ending calculation in several cases![]()
图 3 方案4下不同折减系数塑性区发展过程Figure 3. The development progress of plastic zone in reduction factors of case 4对比水合物带分解60%之后的水合物带强度与边坡均质土层强度，发现两者弹性模量、泊松比等强度参数特征相似，可以认为60%分解程度下的水合物带强度略低于边坡均质土层强度，两者强度关系对于分析塑性区发展过程十分重要。在此强度下的方案4计算过程中塑性区发展过程与之前所述方案明显不同。该方案下，如图 3a所示，塑性区首先在坡脚位置出现，紧接着在模型右侧和水合物带出现，而不是自坡脚逐渐向上发展。随着分析的进行，坡脚的塑性区逐渐向上发展至水合物带，水合物带的塑性区同时向上发展至坡顶，形成贯通的塑性区，如图 3b。此时塑形贯通区的形成并没有直接导致计算中止，折减系数进一步增大时，一个新的塑性带自坡脚发展至坡顶，并最终形成另一个较弱的塑性贯通区，即形成了2个塑性贯通区。如图 3c所示。随着折减系数继续增加，2个塑性区大部分合二为一，但仍存在小部分的间隔区域。
通过位移云图可以更加直观地认识边坡最终状态和具体失稳程度，图 3c与图 4c为同一折减系数，同为计算终止时的状态，可以发现2种云图的对应关系。同时，列举了几个方案下的位移云图，与图 2对比分析发现，水合物分解程度越高，滑坡区域的位移越大，即失稳程度越高。
![]()
图 4 部分方案下计算终止时位移云图Figure 4. Contours of displacement in horizon direction when ending calculation in several cases最后3种方案下，塑性区均是首先出现在水合物带，然后出现在坡脚位置。水合物带塑性区向上发展至坡顶，坡脚位置塑性区发展至水合物带，形成塑性贯通区。由于此3种方案下，水合物带强度已显著低于沉积层强度，因此，没有出现方案4相似的二次滑坡问题。前3种方案下，边坡失稳规模取决于其本身强度，后4种方案下，边坡失稳规模取决于水合物带所处的位置。因此，水合物分解直接影响边坡的稳定性及失稳规模。
各方案下安全系数如图 5所示。由于塑性区域总是发生在边坡强度最低或应力分布最集中的位置，前3个方案下均质沉积层的强度低于水合物带的强度，因此，安全系数保持不变。自方案4开始，水合物带分解后的强度低于沉积层的强度，安全系数取决于水合物带的强度。安全系数随水合物带强度的不断降低而降低，并最终小于1，这意味着随着水合物的分解，海底边坡会发生大规模滑坡。对比方案6及方案7的安全系数可以发现，边坡的安全系数不仅受边坡强度影响，还与边坡低强度带的规模相关，即局部小规模水合物带的高度分解对整个边坡的安全系数影响程度显著。与马云[19]、于桂林[20]、张振飞[21]等模拟所得结果进行对比，虽然各研究中地层强度参数、边坡模型尺寸、本构模型以及失稳准则等均有差异，但水合物分解前后所得安全系数不存在数量级之间的差异，且随水合物分解，安全系数的变化呈相同趋势。
3.2 不同上覆厚度下水合物带分解对边坡稳定性影响
在图 1所示的基本模型的基础上，只改变图 4模型中水合物带的竖直方向的位置，调整水合物带上覆沉积层的厚度，建立3个新模型，同时将基本模型纳入分析，每个模型根据水合物分解程度分别进行2次计算。具体计算方案如表 5所示。
表 5 水合物层不同上覆厚度下计算方案Table 5. Numerical procedure under different overlay thickness of hydrate计算模型 上覆沉积层厚度/m 水合物分解程度 模型1 50 未分解 1区域分解100%，2区域分解80%，3区域分解60%，4区域分解30% 模型2 80 模型3 120 模型4 150 当水合物带未分解时，水合物带相当于一个坚硬的夹层，边坡失稳的程度、规模以及安全系数取决于边坡自身的强度。但是其埋藏程度对边坡稳定性仍有一定影响。图 6反映了水合物未分解时的边坡失稳特征。当水合物带埋深低于边坡自身可能失稳时的滑坡深度时，具有较高强度的水合物带会限制边坡失稳的规模，但是对安全系数几乎没有影响。当水合物带埋深较深时，水合物带的存在对边坡自身稳定性几乎没有影响，但对边坡抵抗地质灾害的能力有所提升。
![]()
图 6 不同上覆厚度下水合物带未分解计算终止时位移云图Figure 6. Displacement contours of slope without hydrate dissociation under different overlay thickness由图 7可以看出，随着水合物带的分解，塑性区域总是会贯通整个水合物带，水合物带上部区域都是潜在的滑坡区域。边坡产生横向位移区域的下边界与塑性贯通区下边界是同一个边界。因此，横向位移云图不仅能反映边坡失稳的区域和规模，还能反映失稳的强度。对比各方案发现，塑性区总是可以贯通水合物带和坡脚坡顶，上覆沉积层厚度的不同直接导致滑坡规模的不同。随着上覆沉积层厚度的增加，边坡失稳区域随之增加。这种增加不仅仅表现为厚度的增加，坡顶失稳的范围也逐渐向内部发展。这是由于分解后的水合物带强度低于沉积土层所致。
![]()
图 7 不同上覆厚度下水合物带分解计算终止时横向位移云图Figure 7. Horizontal displacement contours of slope when ending calculation with different overlay thickness安全系数与水合物带埋深关系曲线如图 8所示，水合物未分解情况下，边坡的安全系数保持稳定；水合物带分解至低于沉积层强度时，随着上覆岩层厚度的增加，安全系数增加，且失稳的规模也增加。可能的原因是：水合物带分解后强度大幅降低后，塑形区总是会贯穿整个水合物层。上覆岩层厚度的增加，塑性贯通区以上所包含的均质沉积层的规模增大，所需能量越多，抵抗由于下部水合物带强度降低所引起的失稳的能力越大，导致安全系数逐渐上升。其具体原因有待进一步分析论证。根据图 8所示的两条曲线发展趋势，基本可以确定不同埋深条件下，水合物分解与未分解情况所得安全系数会存在交点。此时，水合物分解与否不会对边坡的稳定性产生影响，对边坡稳定性产生影响的只能是沉积层自身强度。同样，此规律尚无成型的数学预测模型，有待于进一步研究。
3.3 水合物带分解对不同角度边坡稳定性影响
在如图 1所示的基本模型的基础上，改变图 3-1模型中边坡角度，对应调整边坡左侧高度。本小节中共采用4个模型，其边坡角度分别是10°、15°、20°、25°，水合物带保持与边坡斜边平行，每个模型根据水合物分解程度分别进行2次计算。具体计算方案如表 6所示。
表 6 不同边坡角度的模型计算方案Table 6. Numerical procedure with different slope angel计算模型 边坡角度/(°) 水合物分解程度 模型5 10 未分解 1区域分解100%，2区域分解80%，3区域分解60%，4区域分解30% 模型6 15 模型7 20 模型8 25 水合物分解前后模拟结果如图 9、图 10所示，其中，边坡角度为20°时，水合物分解前、后云图分别见图 6c、图 7c。可以发现，边坡角度对边坡安全系数影响很大，但是对边坡可能的失稳规模影响不大。因为塑形区是连接整个水合物带和坡脚、坡顶的，在水合物带相对位置相同的情况下，塑形贯通区以上的失稳区域也大致相当。图 11所示为水合物分解前后不同角度下边坡的安全系数，随着边坡角度的增加，边坡的安全系数本身会有一个较大幅度的变化，但总是大于1(小于1意味着自然失稳)。正是由于水合物的分解作用，分解后水合物安全系数降至1以下，说明水合物分解对边坡稳定性影响显著, 同时说明在较大角度的海底斜坡上开采水合物风险很大，应充分评估其失稳可能性。
![]()
图 9 不同上覆厚度下水合物带未分解计算终止时位移云图Figure 9. Displacement contours of slope under different slope angle without hydrate dissociation![]()
图 10 不同边坡角度下水合物带未分解计算终止时横向位移分布云图Figure 10. Horizontal displacement contours when ending calculation under different slope angle4. 结论
(1) 塑性区域发展过程。正常情况下，塑性区自坡脚区域向上发展，形成塑形贯通区；水合物分解程度达到60%后，塑性区会先后出现在水合物带和坡脚区域，水合物带的塑性区向上发展至坡顶，坡脚区域的塑性区向上发展至水合物带，最终形成塑形贯通区。
(2) 水合物分解程度达到60%及以上，整个边坡的安全系数会降低，并最终失稳。分解程度越高，边坡失稳时的安全系数越小。
(3) 水合物未分解情况下，水合物带的存在有利于维持边坡稳定；水合物充分分解条件下，水合物埋深越深，整个边坡的安全系数越高。大角度边坡水合物开采风险较大。
-
![]()
图 2 部分方案计算终止时塑性区分布云图
Figure 2. Contours of plastic zone when ending calculation in several cases
![]()
图 3 方案4下不同折减系数塑性区发展过程
Figure 3. The development progress of plastic zone in reduction factors of case 4
![]()
图 4 部分方案下计算终止时位移云图
Figure 4. Contours of displacement in horizon direction when ending calculation in several cases
![]()
图 6 不同上覆厚度下水合物带未分解计算终止时位移云图
Figure 6. Displacement contours of slope without hydrate dissociation under different overlay thickness
![]()
图 7 不同上覆厚度下水合物带分解计算终止时横向位移云图
Figure 7. Horizontal displacement contours of slope when ending calculation with different overlay thickness
![]()
图 9 不同上覆厚度下水合物带未分解计算终止时位移云图
Figure 9. Displacement contours of slope under different slope angle without hydrate dissociation
![]()
图 10 不同边坡角度下水合物带未分解计算终止时横向位移分布云图
Figure 10. Horizontal displacement contours when ending calculation under different slope angle
物理量 数值 单位 c1 293 kPa c2 1960 kPa c3 1.7 σ′3 1962 kPa σ′t 382 kPa δ1 0.4 δ2 0.2 δ3 0.22 δ4 0.04 e 2.72 e1 548000 kPa e2 265800 kPa e3 450000 kPa γ 
下载: 导出CSV
表 2 神狐海域水合物地层勘探数据及数值模型选用数据(据文献[1, 19, 35, 42])
Table 2 Exploration data and numerical model selected data for hydrate formations in the Shenhu area
参数 神狐海域勘探数据 模型选用数据 水深/m 500~2000 1300~1650 水合物埋深/m 7~350 50~150 海底坡脚/(°) 最高达30 10~25 颗粒密度/(g/cm3) 2.695~2.716 2.700 海水密度/(g/cm3) 1.040 1.040 水合物密度/(g/cm3) 0.980 0.980 水合物饱和度 0.45~0.92 0.8 沉积物孔隙度 0.27~0.63 0.4
下载: 导出CSV
表 3 模型材料强度参数
Table 3 Strength parameters of numerical model
材料 内聚力
/kPa摩擦角
/(°)杨氏模量
/MPa密度
/(g/cm3)沉积层 291.2 18.6 56.3 2.200 水合物层分解程度 未分解 1562.9 26.0 206.0 1.844 分解30% 504.2 22.7 89.7 1.794 分解60% 308.6 19.4 41.2 1.745 分解80% 89.2 17.3 23.7 1.711 分解100% 35.4 15.2 10.28 1.688
下载: 导出CSV
表 4 模拟方案设计
Table 4 Conceptual design of simulation
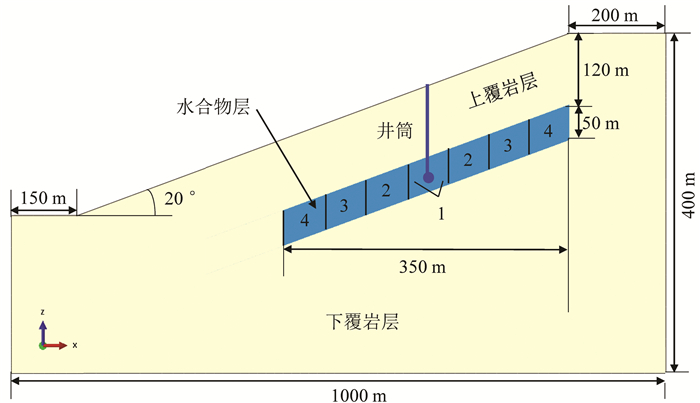
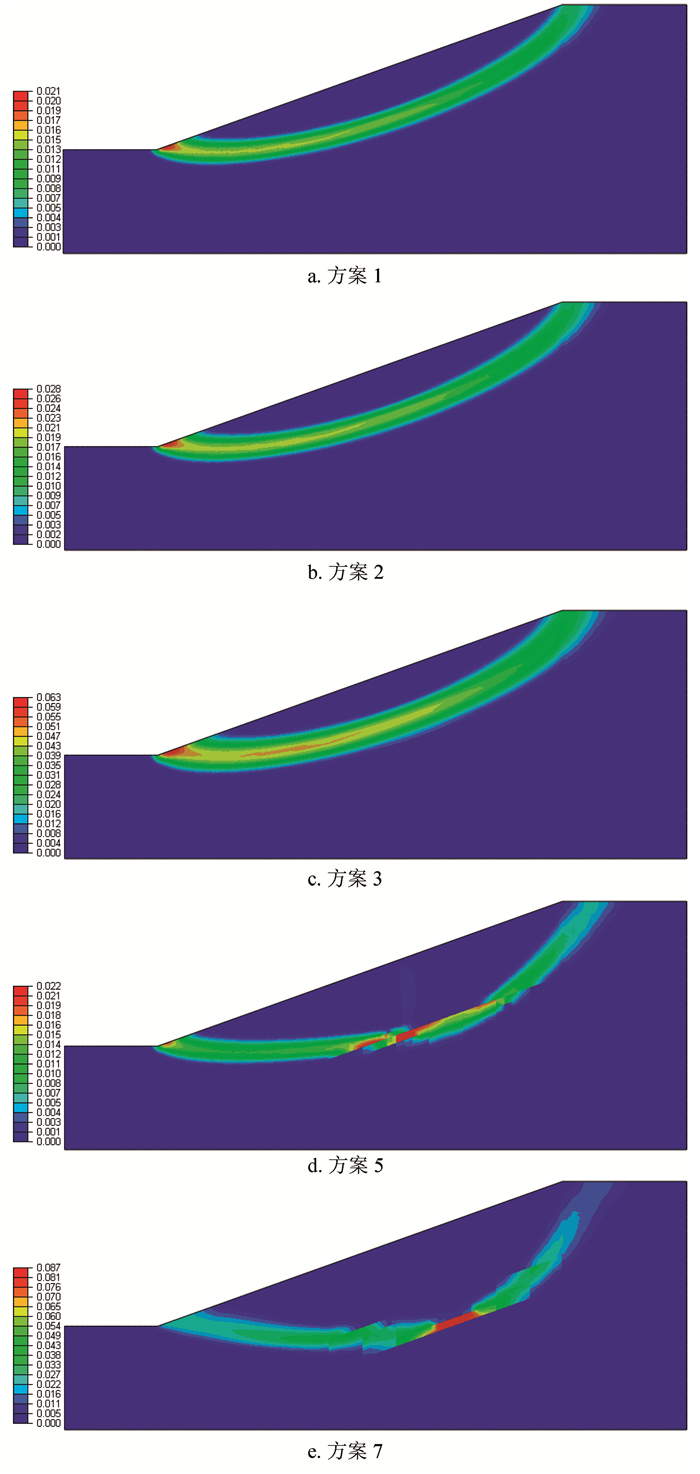
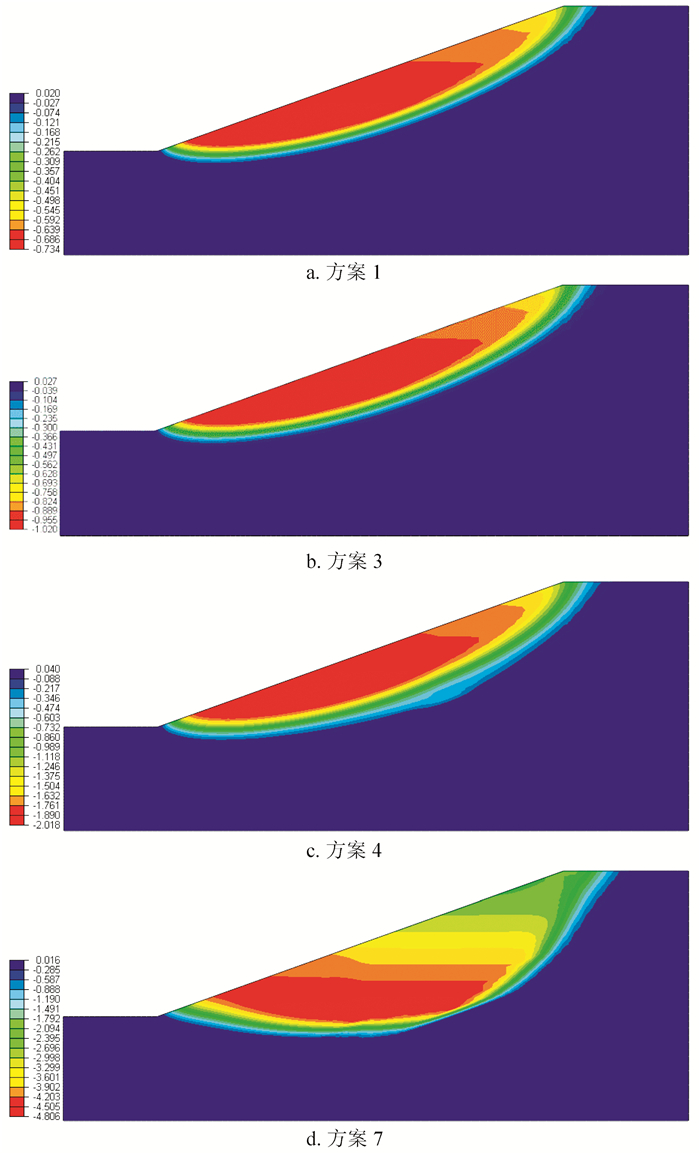
方案 方案描述 方案1 不含水合物层的均质海底边坡模型 方案2 含水合物且水合物未分解的海底边坡模型 方案3 1区分解30%，其他区域未分解 方案4 1区分解60%，2区分解30%，其他区域未分解 方案5 1区分解80%，2区分解60%，3区分解30%，4区未分解 方案6 1区分解100%，2区分解80%，3区分解60%，4区分解30% 方案7 1、2区分解100%，3、4区分解80%
下载: 导出CSV
表 5 水合物层不同上覆厚度下计算方案
Table 5 Numerical procedure under different overlay thickness of hydrate
计算模型 上覆沉积层厚度/m 水合物分解程度 模型1 50 未分解 1区域分解100%，2区域分解80%，3区域分解60%，4区域分解30% 模型2 80 模型3 120 模型4 150
下载: 导出CSV
表 6 不同边坡角度的模型计算方案
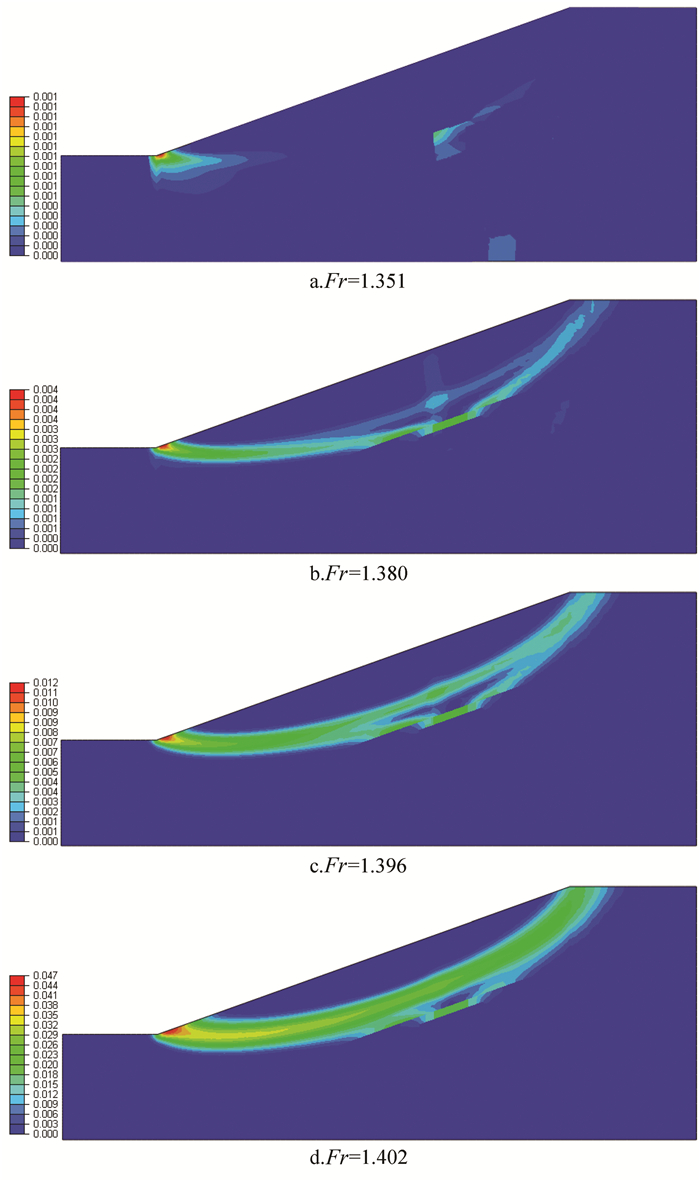
Table 6 Numerical procedure with different slope angel
计算模型 边坡角度/(°) 水合物分解程度 模型5 10 未分解 1区域分解100%，2区域分解80%，3区域分解60%，4区域分解30% 模型6 15 模型7 20 模型8 25
下载: 导出CSV
-
[1] 何静, 刘学伟, 杨萌萌, 等.海底未固结成岩地层体积密度的估算方法[J].海洋地质与第四纪地质, 2011, 31(5):155-161. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=9aec573c-4ced-4d05-87be-ec13233b406e HE Jing, LIU Xuewei, YANG Mengmeng, et al. Estimate bulk density of unconsolidated sea-bottom sediments[J]. Marine Geology & Quaternary Geology, 2011, 31(5):155-161. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=9aec573c-4ced-4d05-87be-ec13233b406e
[2] 胡高伟, 李彦龙, 吴能友, 等.神狐海域W18/19站位天然气水合物上覆层不排水抗剪强度预测[J].海洋地质与第四纪地质, 2017, 37(5):151-158. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=3ffe2a0c-682f-445c-b9ff-399376219619 HU Gaowei, LI Yanlong, WU Nengyou, et al. Undrained shear strength estimation of the cover layer of hydrate at site W18/19 of Shenhu area[J]. Marine Geology & Quaternary Geology, 2017, 37(5):151-158. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=3ffe2a0c-682f-445c-b9ff-399376219619
[3] 叶黎明, 罗鹏, 杨克红.天然气水合物气候效应研究进展[J].地球科学进展, 2011, 26(5):565-574. http://d.old.wanfangdata.com.cn/Periodical/dqkxjz201105012 YE Liming, LUO Peng, YANG Kehong. Advances in climatic effects study of gas hydrates[J]. Advances in Earth Science, 2011, 26(5): 565-574. http://d.old.wanfangdata.com.cn/Periodical/dqkxjz201105012
[4] Kvenvolden K A. Gas hydrates—geological perspective and global change[J]. Reviews of Geophysics, 1993, 31(2):173-187. https://www.researchgate.net/publication/251431257_Gas_hydrates-Geological_perspective_and_global_change
[5] Kurihara M, Sato A, Ouchi H, et al. Prediction of gas productivity from eastern Nankai Trough methane hydrate reservoirs[C]//Offshore Technology Conference. Offshore Technology Conference, 2008.
[6] White M D, McGrail B P. A new numerical simulator for analysis of methane hydrate production from geologic formations[C]//Proceedings of 2nd International Symposium on Gas Hydrate Technology, 2006: 1-2.
[7] Moridis G J. A code for the simulation of system behavior in hydrate-bearing geologic media[J]. Stereochemical & Stereophysical Behaviour of Macrocycles, 2014, 10(2): Ⅳ.
[8] Moridis G J, Collett T S, Pooladi-Darvish M, et al. Challenges, uncertainties and issues facing gas production from gas hydrate deposits[J]. SPE Reservoir Evaluation & Engineering, 2011, 14(1):76-112. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0223144391/
[9] 朱超祁, 贾永刚, 刘晓磊, 等.海底滑坡分类及成因机制研究进展[J].海洋地质与第四纪地质, 2015, 35(6):145-155. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=886d250b-1f44-45ef-b85d-20279449219d ZHU Chaoqi, JIA Yonggang, LIU Xiaolei, et al. Classification and genetic mechanism of submarine landslide: A review[J]. Marine Geology & Quaternary Geology, 2015, 35(6):145-155. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=886d250b-1f44-45ef-b85d-20279449219d
[10] 吴能友, 黄丽, 胡高伟, 等.海域天然气水合物开采的地质控制因素和科学挑战[J].海洋地质与第四纪地质, 2017, 37(5):1-11. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=7ac0922f-09a0-4694-a851-841b8fc0bf7f WU Nengyou, HUANG Li, HU Gaowei, et al. Geological controlling factors and scientific challenges for offshore gas hydrate gas hydrate exploitation[J]. Marine Geology & Quaternary Geology, 2017, 37(5):1-11. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=7ac0922f-09a0-4694-a851-841b8fc0bf7f
[11] Li S, Xu X, Zheng R, et al. Experimental investigation on dissociation driving force of methane hydrate in porous media[J]. Fuel, 2015, 160:117-122. doi: 10.1016/j.fuel.2015.07.085
[12] Kamath V A. A perspective on gas production from hydrate[C]// The JNOC's Methane Hydrate International Symposium. Chiba City: Japan National Oil Corporation, 1998: 87-92.
[13] Gupta S, Deusner C, Haeckel M, et al. Testing a thermo-chemo-hydro-geomechanical model for gas hydrate-bearing sediments using triaxial compression laboratory experiments[J]. Geochemistry, Geophysics, Geosystems, 2015, 77(9):229-250. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=3f888c8f531f0528ca6ceaefa5ef7703
[14] Sultan N, Cochonat P, Foucher J P, et al. Effect of gas hydrates melting on seafloor slope instability[J]. Marine Geology, 2004, 213(1):379-401. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=95178084483c365060cb5925a823a9c3
[15] Gupta S, Wohlmuth B, Helmig R. Multi-rate time stepping schemes for hydro-geomechanical model for subsurface methane hydrate reservoirs[J]. Advances in Water Resources, 2016, 91: 78-87. doi: 10.1016/j.advwatres.2016.02.013
[16] Lu L, Zhang X H, Lu X B. Numerical study on the stratum's responses due to natural gas hydrate dissociation[J]. Ships and Offshore Structures, 2017, 12(6): 775-780. doi: 10.1080/17445302.2016.1241366
[17] 周丹.天然气水合物分解对海底结构物稳定性影响的研究[D].大连理工大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10141-1012394319.htm ZHOU Dan. Study on the influence of the seabed structure stability due to natural gas hydrate dissociation[D]. Dalian University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10141-1012394319.htm
[18] 杨晓云.天然气水合物与海底滑坡研究[D].中国石油大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10425-2010280307.htm YANG Xiaoyun. Study of gas hydrate and submarine landslide[D]. China University of Petroleum, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10425-2010280307.htm
[19] 马云.南海北部陆坡区海底滑坡特征及触发机制研究[D].中国海洋大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10423-1014368509.htm MA Yun. Study of submarine landslides and trigger mechanism along the continental slope of the northern South China Sea[D]. Ocean University of China, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10423-1014368509.htm
[20] 于桂林.考虑孔压影响的海底能源土斜坡稳定性分析[D].青岛理工大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10429-1016053926.htm YU Guilin. Stability analysis of submarine energy soil slope considering the influence of pore pressure[D]. Qingdao University of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10429-1016053926.htm
[21] 张振飞.海底能源土斜坡稳定性影响因素的敏感性分析[D].青岛理工大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10429-1017017667.htm ZHANG Zhenfei. Sensitivity analysis of influencing factors on stability of submarine energy soil slope[D]. Qingdao University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10429-1017017667.htm
[22] 刘浩伽, 李彦龙, 刘昌岭, 等.水合物分解区地层砂粒启动运移临界流速计算模型[J].海洋地质与第四纪地质, 2017, 37(5):166-173. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=f66bd1b9-7b64-42c3-9c12-21afa94a75e6 LIU Haojia, LI Yanlong, LIU Changling, et al. Calculation model for critical velocity of sand movement in decomposed hydrate cemented sediment[J]. Marine Geology & Quaternary Geology, 2017, 37 (5):166-173. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=f66bd1b9-7b64-42c3-9c12-21afa94a75e6
[23] Winters W J, Waite W F, Mason D H. Strength and Acoustic Properties of Ottawa Sand Containing Laboratory-Formed Methane Gas Hydrate[M]//Advances in the Study of Gas Hydrates, Springer, Boston, MA, 2004: 213-226.
[24] Yun T S, Santamarina J C, Ruppel C. Mechanical properties of sand, silt, and clay containing tetrahydrofuran hydrate[J]. Journal of Geophysical Research: Solid Earth, 2007, 112:B04106. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1029/2006JB004484
[25] Yun T S, Santamarina J C. Hydrate growth in granular materials: implication to hydrate bearing sediments[J]. Geosciences Journal, 2011, 15(3): 265. doi: 10.1007/s12303-011-0025-9
[26] Waite W F, Santamarina J C, Cortes D D, et al. Physical properties of hydrate-bearing sediments[J]. Reviews of Geophysics, 2009, 47(4), doi: 10.1029/2008RG000279.
[27] Ghiassian H, Grozic J L H. Methane hydrate formation under controlled pressure in conventional triaxial apparatus[C]//Proceedings of the 63rd Canadian Geotechnical Conference, Calgary, Alberta. 2010: 12-16.
[28] Ghiassian H, Grozic J L H. Strength behavior of methane hydrate bearing sand in undrained triaxial testing[J]. Marine and Petroleum Geology, 2013, 43: 310-319. doi: 10.1016/j.marpetgeo.2013.01.007
[29] Winters W J, Waite W F, Mason D H, et al. Methane gas hydrate effect on sediment acoustic and strength properties[J]. Journal of Petroleum Science and Engineering, 2007, 56(1-3): 127-135. doi: 10.1016/j.petrol.2006.02.003
[30] Lin J S, Seol Y, Choi J H. Geomechanical modeling of hydrate-bearing sediments during dissociation under shear[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2017, 41(14): 1523-1538. doi: 10.1002/nag.v41.14
[31] You K, Flemings P B. Methane hydrate formation in thick sand reservoirs: 1. Short-range methane diffusion[J]. Marine and Petroleum Geology, 2018, 89: 428-442. doi: 10.1016/j.marpetgeo.2017.10.011
[32] Pinkert S, Grozic J L H. Prediction of the mechanical response of hydrate-bearing sands[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(6): 4695-4707. doi: 10.1002/2013JB010920
[33] Pinkert S, Grozic J L H. An analytical-experimental investigation of gas hydrate-bearing sediment properties[C]//Canadian Geotechnical Conference and the 11th Joint CGS/IAHCNC Ground Water Conference, 2013.
[34] Miyazaki K, Masui A, Sakamoto Y, et al. Triaxial compressive properties of artificial methane-hydrate-bearing sediment[J]. Journal of Geophysical Research: Solid Earth, 2011, 116(B6). http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_ee192397b0aa10dfd760be67479508ab
[35] 邬黛黛, 谢瑞, 杨睿, 等.南海北部神狐海域水合物钻探区沉积物地球化学特征[J].海洋地质与第四纪地质, 2017, 37(6):100-109. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=99ac3f58-cd4d-43ae-a179-d9c60a800929 WU Daidai, XIE Rui, YANG Rui, et al. Geochemistry of the sediments in Shenhu hydrate drilling area, South China Sea[J]. Marine Geology & Quaternary Geology, 2017, 37(6):100-109. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=99ac3f58-cd4d-43ae-a179-d9c60a800929
[36] 李广信.高等土力学[M].清华大学出版社有限公司, 2004. LI Guangxin. Advanced Soil Mechanical[M]. Tsinghua University Press Co, Ltd, 2004.
[37] Coleman J M, Garrison L E. Geological aspects of marine slope stability, northwestern Gulf of Mexico[J]. Marine Georesources & Geotechnology, 1977, 2(1-4): 9-44. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1080/10641197709379769
[38] Fredlund D G, Krahn J. Comparison of slope stability methods of analysis[J]. Canadian Geotechnical Journal, 1977, 14(3): 429-439. doi: 10.1139/t77-045
[39] Zienkiewicz O C, Humpheson C, Lewis R W. Discussion: Associated and non-associated visco-plasticity and plasticity in soil mechanics[J]. Geotechnique, 1977, 27(1): 101-102. doi: 10.1680/geot.1977.27.1.101
[40] 费康, 张建伟. ABAQUS在岩土工程中的应用[M].中国水利水电出版社, 2010. FEI Kang, ZHANG Jianwei. Application of ABAQUS in Geotechnical Engineering[M]. China WaterPower Press, 2010.
[41] Kim A R, Kim H S, Cho G C, et al. Estimation of model parameters and properties for numerical simulation on geomechanical stability of gas hydrate production in the Ulleung Basin, East Sea, Korea[J]. Quaternary International, 2017, 459:55-68. doi: 10.1016/j.quaint.2017.09.028
[42] 杨涛, 叶鸿, 赖亦君.南海北部陆坡天然气水合物的沉积物孔隙水地球化学研究进展[J].海洋地质与第四纪地质, 2017, 37(5):48-58. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=86191583-ebd6-4ca4-bf79-024ff81d7dc7 YANG Tao, YE Hong, LAI Yijun. Pore water geochemistry of the gas hydrate bearing zone on northern slope of the South China Sea[J]. Marine Geology & Quaternary Geology, 2017, 37(5):48-58. http://hydz.chinajournal.net.cn/WKD/WebPublication/paperDigest.aspx?paperID=86191583-ebd6-4ca4-bf79-024ff81d7dc7
[43] Jin G, Xu T, Xin X, et al. Numerical evaluation of the methane production from unconfined gas hydrate-bearing sediment by thermal stimulation and depressurization in Shenhu area, South China Sea[J]. Journal of Natural Gas Science and Engineering, 2017, 33: 497-508. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a6b711878e75d49e8580a0570ce09b98
[44] Jin G, Lei H, Xu T, et al. Simulated geomechanical responses to marine methane hydrate recovery using horizontal wells in the Shenhu area, South China Sea[J]. Marine and Petroleum Geology, 2017, 92: 424-436. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=39ffd28290d57dbfd43ba0fd91bb5060
-
期刊类型引用(3)
1. 王辉，修宗祥，孙永福，刘绍文，宋玉鹏，董立峰，宋丙辉. 考虑天然气水合物上覆层不排水抗剪强度深度变化的海底斜坡稳定性影响分析. 高校地质学报. 2022(05): 747-757 . 
百度学术
2. 胡志刚，周湘君，周恺. 反倾互层岩质边坡挖方稳定性的建模分析. 水力发电. 2022(12): 37-41 . 百度学术
3. 赵亚鹏，孔亮，刘乐乐，袁庆盟，刘佳棋. 基于两步折减法的含天然气水合物沉积物海底斜坡稳定性分析. 天然气工业. 2021(10): 141-153 . 百度学术
其他类型引用(9)
计量
- 文章访问数: 3212
- HTML全文浏览量: 714
- PDF下载量: 75
- 被引次数: 12
