PROGRESS OF NUMERICAL MODELING OF EARLY DIAGENESIS AND METHANE ANAEROBIC OXIDATION
-
摘要: 在海洋沉积物表层,各种碳库之间频繁的碳转换引起了越来越多科学家的关注。这些转换主要包括有机质降解生成的DIC,甲烷缺氧氧化产生DIC,以及碱度升高引起的自生碳酸盐沉淀,同时在一些甲烷强烈渗漏的冷泉区还包括游离气的渗漏过程。这些反应发生机理将在本文中逐一论述,同时文中还综述了有机质降解和甲烷缺氧氧化过程的现有计算模型,指出了目前计算模型中所存在的缺陷及每个模型的适用范围,并简要的介绍了从沉积物释放到海水中的甲烷气泡渗漏通量计算方法。然而这些模型基本都受限于目前对于机理的认识水平,为了更加精确地计算出碳在不同过程中的转换通量,今后还需要更多的工作来研究反应机理和模型中的参数,从而获得一个更加通用的模型。Abstract: Carbon conversion between different reservoirs in the surface sediments has raised more and more attention from researchers. It mainly includes the dissolved inorganic carbon (DIC) produced by organic matter degradation and anaerobic oxidation of methane (AOM) as well as authigenic carbonate precipitation. In some intensive seepage area, gas bubble migration and dissolution is also an important carbon conversion pathway. In this paper, we summarize the mechanism of organic matter degradation and AOM through numerical modeling. In addition, upon the discussion on the shortages and applicability of each model, we introduced the method of quantification of gas bubble flux into seawater. We finally proposed that more attention be paid to the mechanism of the biogeochemical processes and the model parameters for developing a more generalized model, in order to obtain a more reliable and convincing carbon turnover modeling results.
-
Keywords:
- sediment-seawater /
- interface /
- organic degradation /
- methane anaerobic oxidation /
- numerical model
-
碳作为我们生命中不可替代的重要角色,它承担着生命骨架的作用,同时为人类生活提供充足的能源和适宜的气候条件[1]。正因为此,碳的来源、运输转化和储存一直是全球科学家们普遍关心的重大科学问题。自从工业革命以来,大气中已经积累了240 Pg的碳[2]。这些碳主要来自人类化石燃料的使用和石灰的煅烧,还有少部分的来自于土壤的呼吸、火山和动物的呼吸排泄等。其中部分二氧化碳会溶解于海洋中,并且通过洋流和表层水团与深层水团交换的方式促进了海洋表层二氧化碳的溶解。通过海洋中CO2分压和O2/N2比率变化测算,每年海洋吸收的碳为1~3.2 Pg,其中储存在海水中的碳为3.8×104 Pg[2, 3]。海水表层的二氧化碳虽然难以通过溶解扩散的方式运送到海洋深部,但是在真光层内溶解的二氧化碳却是海水中藻类的重要碳源。海洋藻类通过光合作用将溶解无机碳转化为颗粒有机碳,同时释放氧气。海水表层初级生产力生成的大量颗粒有机碳(POC:Particulate Organic Carbon),大部分在海水中被微生物降解转化成CO2和惰性溶解有机碳,仅有20%的POC沉降到海底[4]。海水表层的碳就是以这种方式向深海和海底输运[5]。沉降到海底的POC会进一步被底栖微生物利用,只有少部分的POC被最终埋藏。尽管埋藏在沉积物中POC相比于初级生产力小很多,但它在调节地质历史时期大气CO2和O2的量起非常重要的作用,是地球系统碳循环的核心组成部分[6]。
POC沉降到海底后,在微生物参与下,先后发生一系列与有机质降解相关的生物地球化学反应,包括有机质有氧氧化、反硝化作用、铁锰氧化物-有机质氧化作用、有机质硫酸盐还原作用、产甲烷作用。这些反应发生的顺序主要由释放吉布斯自由能所决定。由于有机质降解的最终反应是产甲烷作用,故沉积物中普遍有生物成因甲烷。另一方面,有机质在经历浅表层的微生物降解后,会被埋藏到沉积层深处,发生热解作用,产生大量热成因甲烷。生物成因甲烷和热成因甲烷在合适的温压条件下,与沉积孔隙中的水生成天然气水合物[7]。这些位于海底沉积物孔隙中的天然气水合物对于碳转化也起到了非常重要的“capacitor”(电容器)作用,在水合物稳定带扩大的时候储存大量的碳,在稳定带减小的时候释放大量的碳[8]。
尽管海底沉积物中蕴含丰富的甲烷,但是极少量的甲烷可以直接进入上覆海水,这主要归因于浅层沉积物的硫酸盐甲烷转换带(SMTZ:Sulfate Methane Transition Zone)中由甲烷厌氧古菌和硫酸盐还原细菌共同作用下的甲烷缺氧氧化-硫酸盐还原耦合作用(AOM:Anaerobic Oxidation of Methane)[9]。据估计,全球海洋沉积物中通过AOM消耗的量约342 Tg CH4/a[10]。只有在甲烷通量足够大,比如水合物分解或油气渗漏等,甲烷会以海底冷泉的方式渗漏出海底。在近30年以来,人们发现这种以水、碳氢化合物(天然气和石油)、硫化氢、细粒沉积物为主的冷泉发育区的碳转换异常频繁,于是引起了人们越来越多的关注[11, 12]。活动冷泉区未被AOM消耗的甲烷在进入海水之前还会在细菌和古菌参与下发生有氧氧化作用,甲烷的有氧和缺氧氧化共同组成“benthicfilter”(底栖过滤层)[13, 14],其对于碳的释放具有非常重要的调控作用。
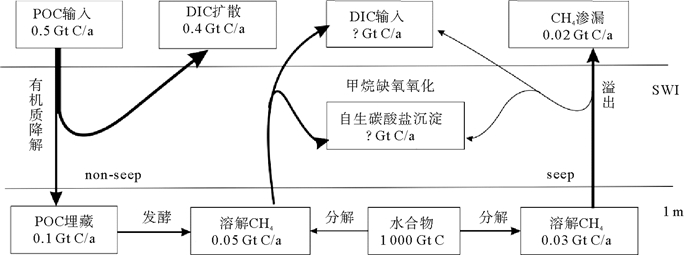
至于这些生物地球化学过程对全球碳循环有多大影响,需要对各种碳储库之间的交换通量有充分的了解。根据现有的研究数据,大陆斜坡地区每年至少沉降0.5 Gt颗粒有机碳(图 1)。其中有80%的有机碳会在沉积物界面之下1 m内被底栖动物和微生物所利用[15, 16],剩余的有机质会以每年0.01~0.02 Gt的速度转化为甲烷[7]。同时由于水合物分解也会增加溶解甲烷碳库,粗略估计每年从水合物区向冷泉区和非冷泉区释放的甲烷都为0.03 Gt[17]。这些溶解甲烷在不同的区域以不同的速率被消耗,其中大部分是以甲烷缺氧氧化的方式转化为溶解无机碳(DIC:Dissolved Inorganic Carbon)或沉淀为自生碳酸盐,而在强渗漏区由于渗漏通量太大,约有0.02 Gt甲烷会被释放到水体或大气中[18]。
上述数据通过实验模拟或原位观测获得不仅费时费力,而且不利于对大的时空尺度通量进行预测。基于目前计算机对于大数据的灵活快速处理,许多对于大尺度的计算得益于数值模拟技术的发展,然而具体的模拟除了数值算法外,主要依赖于数值模型的建立。其中对于早期成岩过程的模型研究,从Berner开始到Boudreau已经形成比较系统的早期成岩模型,并且已经在一些区域得到应用[19-21]。随着实验模拟和野外观测手段的不断进步,这也促使了对早期成岩过程机理有了更深入的理解[22]。然而相对早期成岩过程研究来说,甲烷缺氧氧化过程模型的研究起步较晚。对于该过程的发现和证实主要是通过浓度剖面、放射性同位素示踪,并最终把甲烷和硫酸盐的反应确定为最主要的缺氧氧化过程[23]。虽然目前对于缺氧氧化过程认识还存在争议,但是从简单模型开始,近年来有更多的模型能够较准确地描述甲烷缺氧氧化[17, 24]。相对于前两种生物地球化学过程,由于甲烷气泡溢出现象的时空差异导致其研究状况相对更少。
在对各种碳储库中碳的转换通量的模拟中,其中最主要的在于对数值模型的研究。然而为了要获得一个更加概念化的模型,需要对于反应机理有充分的理解。所以本文主要就从近30年来海底沉积物碳转化的研究成果为基础,综述前人对于海底冷泉区中有机质降解、甲烷缺氧氧化和甲烷渗漏过程中碳转换的生物地球化学过程的认识,并详细总结了早期成岩过程和甲烷缺氧氧化过程主要的数学模型。最后通过指出这些模型的不足来展望今后的研究趋势。
1. 海洋沉积物中有机质降解
1.1 有机质降解过程
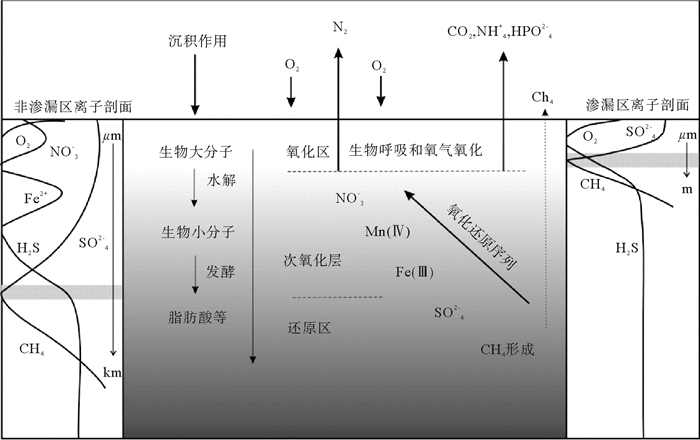
沉积在海底的有机碳大部分来自于陆地和海洋植物的光合作用。其中维管植物会含有大量的纤维素、木质素和复杂的碳水化合物。而海洋生物体中相对富集的是脂质和氮质组分[15]。虽然有机质来源、组成和经历过程不太相同,但沉积物中的有机质却含有相似的组成:10%~20%碳水化合物、10%含氮化合物(如氨基酸)、5%~15%脂类物和剩余的分子式不详的有机质[15]。在非三角洲的大陆架地区,陆源有机质的保存效率是13%左右,而海洋有机质保存效率更低,为1%[15]。总体来说,全球陆坡区至少会沉积0.5 Gt C/a的有机碳[4, 15, 18, 25, 26], 这些碳是底栖生物最重要的食物来源,通过微生物发酵和微生物参与下的氧化还原反应把有机碳最终转化为DIC的形式[15, 27]。栖息在海底顶部1 m的大型生物和活跃微生物对于有机碳的利用效率大约为80%,因此, 对于沉积海底的有机碳每年只有约0.1 Gt能够埋藏下来[7, 28]。沉降有机质在微生物参与下发酵成一系列中间产物,例如碳酸氢根、氨和磷酸(图 2)。在有氧区氧化有机质的终极电子受体为氧气,在次氧化区为硝酸根和铁锰化合物,而在缺氧处电子受体主要由硫酸根和碳酸根充当[29]。通常氧气在沉积物中渗透深度为几毫米至几厘米,氧气的消耗既包括了氧化表层有机质,又包含了缺氧氧化形成的还原产物[25]。有机质硫酸盐还原在沉积物缺氧区是一种重要的生物地球化学反应,消耗了大部分的有机质[29]。从表层起降解反应依次为:
![]() 图 2 有机质降解和甲烷缺氧氧化概念图Figure 2. Schematic graph of organic matter degradation and methane anaerobic oxidation(Middle panel delineates several redox zone in the order of Gibbs energetic potential; dotted point indicates seepage of methane.The faster methane seeps, the sulfate-methane transition zone(shaded area at either side) will be closer to seafloor.Yet in the left panel, sulfate-methane transition zone in non-seep zone usually located deeper than seep area)
图 2 有机质降解和甲烷缺氧氧化概念图Figure 2. Schematic graph of organic matter degradation and methane anaerobic oxidation(Middle panel delineates several redox zone in the order of Gibbs energetic potential; dotted point indicates seepage of methane.The faster methane seeps, the sulfate-methane transition zone(shaded area at either side) will be closer to seafloor.Yet in the left panel, sulfate-methane transition zone in non-seep zone usually located deeper than seep area)有机质有氧氧化:
$$ \begin{array}{*{20}{r}} {2{\rm{C}}{{\rm{H}}_2}{\rm{O}}{{\left( {{\rm{N}}{{\rm{H}}_3}} \right)}_{0.15}}{{\left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right)}_{0.01}} + 2{{\rm{O}}_2} \to }\\ {2{\rm{HCO}}_3^ - + 0.3{\rm{N}}{{\rm{H}}_3} + 0.02{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4} + 2{{\rm{H}}^ + }} \end{array} $$ 反硝化作用:
$$ \begin{array}{l} 10{\rm{C}}{{\rm{H}}_2}{\rm{O}}{\left( {{\rm{N}}{{\rm{H}}_3}} \right)_{0.15}}{\left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right)_{0.01}} + 8{\rm{NO}}_3^ - \to \\ 8{\rm{HCO}}_3^ - + 1.5{\rm{N}}{{\rm{H}}_3} + 0.1{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4} + 2{\rm{C}}{{\rm{O}}_2} + 6{{\rm{H}}_2}{\rm{O}} + \\ 4{{\rm{N}}_2} \end{array} $$ 锰氧化物还原:
$$ \begin{array}{l} 2{\rm{C}}{{\rm{H}}_2}{\rm{O}}{\left( {{\rm{N}}{{\rm{H}}_3}} \right)_{0.15}}{\left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right)_{0.01}} + 4{\rm{Mn}}{{\rm{O}}_2} + \\ 6{{\rm{H}}^ + } \to 2{\rm{HCO}}_3^ - + 0.3{\rm{N}}{{\rm{H}}_3} + 0.02{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4} + 4{\rm{M}}{{\rm{n}}^{2 + }} + \\ 4{{\rm{H}}_2}{\rm{O}} \end{array} $$ 铁氧化物还原:
$$ \begin{array}{l} 2{\rm{C}}{{\rm{H}}_2}{\rm{O}}{\left( {{\rm{N}}{{\rm{H}}_3}} \right)_{0.15}}{\left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right)_{0.01}} + 4{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3} + \\ 14{{\rm{H}}^ + } \to 2{\rm{HCO}}_3^ - + 0.3{\rm{N}}{{\rm{H}}_3} + 0.02{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4} + 8{\rm{F}}{{\rm{e}}^{2 + }}\\ + 8{{\rm{H}}_2}{\rm{O}} \end{array} $$ 有机质硫酸盐还原:
$$ \begin{array}{l} 2{\rm{C}}{{\rm{H}}_2}{\rm{O}}{\left( {{\rm{N}}{{\rm{H}}_3}} \right)_{0,15}}{\left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right)_{0.01}} + {\rm{SO}}_4^{2 - } \to \\ 2{\rm{HCO}}_3^ - + 0.3{\rm{N}}{{\rm{H}}_3} + 0.02{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4} + {{\rm{H}}_2}{\rm{S}} \end{array} $$ 产甲烷作用:
$$ \begin{array}{l} 2{\rm{C}}{{\rm{H}}_2}{\rm{O}}{\left( {{\rm{N}}{{\rm{H}}_3}} \right)_{0.15}}{\left( {{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4}} \right)_{0.01}} \to {\rm{C}}{{\rm{H}}_4} + \\ 0.3{\rm{N}}{{\rm{H}}_3} + 0.02{{\rm{H}}_3}{\rm{P}}{{\rm{O}}_4} + {\rm{C}}{{\rm{O}}_2} \end{array} $$ 1.2 有机质降解模型
有机质的降解、保存和埋藏非常复杂,所以需要运用多学科知识来建立相应的模型,于是反应输运模型(RTM:Reaction-Transport Model)应运而生。这种模型通过简化和抽象旨在描述在大的时间和空间尺度上多种输运和反应过程的相互作用。而目前通过RTM数学表达式还不能够完全描述有机质降解过程,所以通过孔隙水或沉积物剖面数据拟合得到的参数还不能够确切的解释降解过程的一些因素,因此这些参数很难普遍适用。即便如此,RTM模型结果对于认识实测区域有机质降解通量还是有很大意义[30]。
1.2.1 影响模型的因素
目前认为有机质降解主要是受有机质通量、有机质组成、有机质活性、微生物降解、热力学、温度效应、物理保护、大型底栖生物活动和沉积速率因素影响[31-33]。
有机质通量不仅包括海洋真光层中产生的有机质还包括了化能自养生物有机质和通过剥蚀,浊流和底流作用搬运的陆源有机质[34]。但是不同的地区,有机质的输出效率不同,需要人们深入了解有机质输运机制,然后做出合理能量关系模型[35, 36]。输出效率除了与单一的物理输运过程有关外,还和有机质本身的质量和分子结构有很大关系[37, 38]。
微生物在有机质降解中起到了至关重要的作用,海底沉积物中的有机质包含了许多大分子有机质,这些有机质通常不能够被细胞直接利用,而是需要通过胞外水解后再吸收。在不同环境中这些有机质矿化产物的还原性能差异也较大。目前由于很多古菌不能纯培养,所以仍然不知道是哪种微生物在水解和发酵过程中起主要作用[39-41]。
有机质降解还要受到氧化还原反应能量的限制,目前很多研究主要关注的是有机质与终极电子受体(TEA:Terminal Electron Acceptor)反应所释放的能量。这个值不仅依赖于化学结构和碳的氧化状态,还和化合物中键的类型和数量及电子的运行轨迹有密切联系。所以在非标准状态下,TEA的利用顺序可能会有变化[42, 43]。
由于有机质降解是多种酶作用的催化反应,所以温度是制约反应发生的一个重要因素。除此之外,温度对于微生物生理适应、压力选择和反应途径都会产生很大影响。因此短期和长期温度变化对于有机质降解有复杂的影响[44-46]。这就取决于适应环境的微生物种类和有机质降解酶的作用效果[47-49]。
矿物的物理保护能在微观尺度上阻止有机质的降解。目前研究表明这种保护主要有两种形式,直接吸附和共沉淀[31, 50]。它们分别从物理上和化学上抑制了有机质的降解。同时沉积物中的生物扰动会引起物理化学环境变化,从而影响有机质降解速率[51]。除此之外,不同环境中沉积体中碎屑物质的混入效率不同,导致有机质埋藏效率差异,这也能影响有机质降解[32]。
1.2.2 模型建立
以固相和液体相在多孔介质中的一维守恒方程作为控制方程[19],方程如下:
$$ \begin{array}{l} \underbrace {\phi \frac{{\partial {\rm{C}}}}{{\partial {\rm{t}}}}}_{累积速度} = \underbrace {\frac{{\partial \left( {\phi \cdot {{\rm{D}}_{\rm{s}}} \cdot \frac{{\partial {\rm{C}}}}{{\partial Z}}} \right)}}{{\partial Z}}}_{扩散项} - \underbrace {\frac{{\partial \left( {\phi \cdot {{\rm{v}}_{\rm{p}}} \cdot {\rm{C}}} \right)}}{{\partial Z}}}_{对流项} + \\ \underbrace {\phi \alpha \left( {{\rm{C}}\left( 0 \right) - {\rm{C}}} \right)}_{生物灌洗项} + \underbrace {\phi \sum {\rm{R}} }_{反应项} \end{array} $$ (液相1) $$ \begin{array}{l} \underbrace {\left( {1 - \phi } \right)\frac{{\partial G}}{{\partial {\rm{t}}}}}_{累积速度} = \underbrace {\frac{{\partial \left( {\phi \cdot {{\rm{D}}_{\rm{s}}} \cdot \frac{{\partial {\rm{C}}}}{{\partial Z}}} \right)}}{{\partial Z}}}_{生物扰动项} - \underbrace {\frac{{\partial \left( {(1 - \phi ) \cdot {{\rm{v}}_{\rm{s}}} \cdot {\rm{G}}} \right)}}{{\partial Z}}}_{沉积项}\\ + \underbrace {\left( {1 - \phi } \right) \cdot \sum {\rm{R}} }_{反应项} \end{array} $$ (固相2) 反应模型:
(1) 速率法则
假定有机质充足,有机质的降解是一个单步反应,那么反应就会受到特定的速率限制。因此,针对单步反应都采用米氏化学反应动力方程来描述[20, 52]。描述为:
$$ {R_G} = {v_{\max }} \cdot \frac{G}{{{K_{m,G}} + G}} $$ vmax指有机质降解的最大反应速度,Km, G指反应速度为最大速度一半时有机质的量,因为在一定环境中该值为一固定常数,所以称之为半饱和常数。
这种酶催化的动力方程中的常用半饱和常数Km, G来计算有机质降解速率。由于G比Km, G小得多,所以:
$$ {R_G} = k \cdot G\quad k = \frac{{{v_{\max }}}}{{{K_{m,G}}}} $$ (3) k为反应速率常数。
在不同的环境条件下,有机质的降解受到不同的因素所限制。这些因素中能用数学公式来描述的有TEA浓度、电子受体的相互抑制、生物能量、温度和微生物的竞争等因素[53, 54]。其中下标i代表第i步反应,这些影响因素的数学描述按顺序依次如下:
$$ {F_{TEA,i}} = \frac{{TE{A_i}}}{{{K_{m,TE{A_i}}} + TE{A_i}}} $$ (4) TEAi指第i种电子受体的浓度,Km, TEAi为半饱和常数。
$$ {F_{in,i}} = \sum\nolimits_{j = 1}^{i - 1} {\frac{{{K_{in,j}}}}{{{K_{in,j}} + TE{A_j}}}} $$ (5) Kin, j指由于能量释放大小导致不同电子受体之间相互抑制的抑制常数。
$$ {F_{T,i}} = 1 - \exp \left( {\frac{{\Delta {G_{r,i}} + {m_i}\Delta {G_{ATP}}}}{{{\chi _i}RT}}} \right) $$ (6) ΔGr, i指反应标准吉布斯自由能,ΔGATP为合成ATP的最小能量,mi为反应产生ATP数,χi指反应平均化学计量数。
$$ {F_{TEM}} = {e^{ - \left( {{E_a}/RT} \right)}} $$ (7) Ea指反应活化能。
$$ \begin{array}{l} {F_{BIO,i}} = \sum\nolimits_j {{X_j}} \\ \frac{{\partial {B_j}}}{{\partial t}} = {Y_j} \cdot {R_{TEA,i,j}} - {\mu _{dec,j}} \cdot {B_j} \end{array} $$ (8) Yj指微生物的最大生长速率,μdec, j为最大分解速率,RTEA, i, j指有机质的氧化还原速率。
不同环境受限的因素不同,所以在速率计算中添加的项也可以不同。但是综合上述影响因子可以描述为:
$$ \begin{array}{*{20}{l}} {{R_G} = \sum\nolimits_i {{R_i}} }\\ {{R_i} = k \cdot {F_{TEM}} \cdot G \cdot {F_{BIO,i}} \cdot {F_{TEA,i}} \cdot {F_{IN,i}} \cdot {F_{T,i}}} \end{array} $$ (9) (2) 离散模型
上述的k代表有机质的降解性质,通常会受到多种因素的影响,如深度、有机质活性、微生物群落、温度等。如果不同有机质降解性差异不超过一个数量级,那么有机质可以看成一个整体,有机质降解可以用1-G模型来描述[33]。然而沉积物中有机质降解性差异较大,因此,不能利用1-G模型来描述从早期到晚期的整个降解过程。为了描述不同埋藏时期的有机质降解过程,目前普遍采用multi-G模型[55]。该模型是基于有机质中组分不同和降解性差异的假设建立。用方程描述如下:
$$ \begin{array}{*{20}{l}} {{R_G}(t) = k(t) \cdot G(t) = \sum\nolimits_i { - {k_i} \cdot {G_i}(t)} }\\ {{f_i}(t) = \frac{{{G_i}(t)}}{{\sum\nolimits_i {{G_i}(t)} }}} \end{array} $$ (10) 其中ki指代有机质组分i的降解速率常数,而fi指的是有机质的相对系数。这个式子也能够加上速率法则中其他影响因子。理论上把有机质组分分为活性和惰性组分两种,但目前为了区分观测数据,把有机质按降解性难易程度分成3部分。其中k2为10-3/a, k1为1~101/a,k0约为10[21, 54]。
(3) 连续模型
假设有机质组分的活性连续分布,因此, 反应速率描述为:
$$ {R_{(t)}} = - \int\limits_0^\infty {k \cdot g(k,t){\rm{d}}k} $$ g(k, t)代表t时刻,有机质降解性在k到k+dk之间的活性有机质浓度,如果每种有机质都是一级动力,那么:
$$ {R_{(t)}} = - \int\limits_0^\infty {k \cdot g(k,0) \cdot {e^{ - kt}}{\rm{d}}k} $$ gk, 0 代表有机质的原始分布,但目前为止仍不能通过观察得到有机质原始分布状况。在反应连续模型中,通常会采用伽马分布作为有机质的原始分布,描述为[56]:
$$ g(k,0) = \frac{{{g_0} \cdot {k^{v - 1}} \cdot {e^{ - a \cdot k}}}}{{\mathit{\Gamma }(v)}} $$ 其中降解速率常数k是连续变量,而Γ是伽马函数,参数a和v决定了有机质的初始年龄和分布。根据伽马分布的反应连续模型,一级降解速率方程则为[57]:
$$ {R_{(t)}} = k(t) \cdot {G_{(t)}}\;\;\;\;k(t) = v \cdot {(a + t)^{ - 1}} $$ (11) 高v、低a表示有机质较为活性;而低v、高a指示有机质较为惰性。通过对野外数据的统计分析,Middelburg得到一个与上述类似的方程,称为幂函数模型[22]。模型如下:
$$ k(t) = v \cdot {(a + t)^q} $$ (12) Wallmann通过对幂函数模型改进,添加反应产物甲烷和溶解无机碳的抑制项,形成[58]:
$$ k(t) = \frac{{{k_c}}}{{{k_c} + [DIC] + \left[ {C{H_4}} \right]}} \cdot v \cdot {(a + t)^{ - q}} $$ (13) 当在幂函数模型中q等于-1时,幂函数模型中有机质分布符合伽马型。
1.2.3 模型适用性
在有机质降解模型中,有机质的降解性随地区和季节而变化,但考虑最多的因素是生物能量限制,酶的催化动力和底栖大生物的活动。在速率常数的选择上,1-G模型通常描述海底上部有氧层,基本不考虑酶催化动力项和抑制项。而描述包含一定氧化还原序列的深部地层时,模型中须加上酶催化动力和抑制项,同时还要考虑生物的能量限制。生物质生长速度普遍慢于环境的改变速度,所以在环境改变的短暂瞬间有机质情况通常会考虑生物质变化。总的来说,离散模型应用在较浅的沉积地层,一般小于10 m;而连续模型可以运用在较深的地层,最大可以达到10 km[59, 60]。同时,连续模型还常常被用于描述大的地质时间尺度的早期成岩过程[61, 62]。
2. 甲烷缺氧氧化
2.1 甲烷缺氧氧化发生过程
海底沉积物是地球上最大的甲烷储库,含有约5 000 Gt的甲烷碳[63]。如此大的一个碳库一旦释放就会造成全球气候的热事件(如PETM)[64]。通过地球化学、微生物和质量平衡计算的方法证实了在沉积物产生中的90%的甲烷在到达海底之前会通过AOM作用而被消耗[9, 10, 65]。甲烷产生归结于有机质沉积到终端电子受体不可达到的深度,通过发酵作用产生,产生的甲烷然后再通过扩散和对流作用向浅层输运(图 2)。产生的甲烷向上输运,并且与氧化物反应(二次氧化还原反应)。虽然在海洋沉积物中这种氧化还原反应普遍存在,但根据不同的反应和输运速率可以发现氧化还原深度从几厘米到上百米。在该区中甲烷从产甲烷区扩散到海底有氧区之间通常会发生AOM作用。虽然有文章报道甲烷是被硝酸盐或铁氧化物氧化,但是目前普遍认为AOM反应中终端电子受体主要是硫酸根,因为硫酸根浓度是其他氧化剂的20倍[28]。在甲烷氧化古菌和硫酸盐还原菌共同作用的模式中,甲烷和硫酸盐的反应如下:
$$ {\rm{C}}{{\rm{H}}_4} + {\rm{SO}}_4^{2 - } = {\rm{HCO}}_3^ - + {\rm{H}}{{\rm{S}}^ - } + {{\rm{H}}_2}{\rm{O}} $$ 而最新的研究表明甲烷氧化古菌是通过吸收孔隙水中的甲烷和硫酸盐发生氧化还原反应;而硫酸盐还原菌主要是通过歧化单质硫或亚硫化物产生维系生命的能量,这些能量能够被用于同化海水中的无机碳[66]。所以目前认为在共生体中发生的反应如下:
$$ \begin{array}{l} 7{\rm{C}}{{\rm{H}}_4} + 8{\rm{SO}}_4^{2 - } + 5{{\rm{H}}^ + } \to 7{\rm{HCO}}_3^ - + 4{\rm{HS}}_2^ - + \\ 11{{\rm{H}}_2}{{\rm{O}}_{\left( 1 \right)}} \end{array} $$ $$ 4{\rm{HS}}_2^ - + 4{{\rm{H}}_2}{\rm{O}} \to {\rm{SO}}_4^{2 - } + 7{\rm{H}}{{\rm{S}}^ - } + 5{{\rm{H}}^ + } $$ 在活跃冷泉背景下,流体速度越大会促使SMTZ越靠近沉积物-海水界面;而在正常海洋环境中,SMTZ界面会随水深变大从几分米变化到几百米[67]。
2.2 甲烷缺氧氧化模型
由于甲烷缺氧氧化是多种微生物和多种酶共同作用,所以根据不同的影响因素可以得到不同的反应模型。其中最简单的方程是根据反应物浓度得到的经验速率方程,同时还有依不同的代谢反应途径得到的动力模型。
2.2.1 甲烷缺氧氧化的影响因素
除了常说的动力学和热力学的影响因素外,AOM反应还要受到有机质降解、硫酸盐含量和甲烷相态的影响。
海水表层的有机质合成是底栖微生物的重要能量来源,沉积的有机质通量和活性不仅影响到有机质的降解,同时对AOM反应产生一定的影响[11]。这种影响目前还不能够通过模型来进行模拟[68, 69]。有机质的不同活性最终会导致氧化过程热力学参数的不同,不同的热力学数据最终会限制缺氧氧化反应的速率[53],SMTZ深度和∑AOM都和有机质活性密切相关[17]。
硫化氢循环对AOM反应也有一定影响,有机质硫酸盐还原是硫化氢的主要来源,而硫化氢的汇主要有硫化物、单质硫和有机硫[66]。硫化物氧化可以产生中间产物如硫代硫酸根或单质硫,这些产物可以再一次发生歧化反应[11]。产生的硫化氢更易于在氧化区内氧化而不是埋藏作用固定硫。通过地球化学剖面信息是很难区分出这些复杂的氧化还原循环路径,只有通过独立的速率测量和测试模型才能够判断。
大量的硫化氢氧化菌也是控制AOM的重要因素。这些细菌通过吸收硫化氢,然后在氧化带把硫化氢氧化成硫酸根,硫酸根又可以重新被用于有机质氧化和AOM[70]。硫细菌的存在与否还会直接影响到SMTZ界面的深浅[71]。除此之外,埋藏在深部的重晶石溶解和深部卤水侵入也能导致AOM作用,并有可能形成几个SMTZ界面记录[72]。
甲烷水合物和甲烷气体对于AOM速率的影响取决于他们的埋藏深度[66]。同时甲烷水合物的形成本身又受温度、压力和甲烷浓度的影响。在水合物区由于水合物的分解导致大量甲烷的产生,因此, 会导致甲烷以气体方式迁移通过SMTZ界面,或者是由于AOM中消耗甲烷导致气态甲烷的重新溶解从而使得迁移到SMTZ界面的甲烷通量增大[73]。甲烷的相态之间的转化目前普遍采用一种简单的线性公式来进行描述[72]。虽然相态转变对于AOM速率产生重要的影响,但是目前对于其作用的机理还不了解。
2.2.2 模型建立
与有机质降解的RTM一致,在模拟甲烷缺氧氧化速率时方程式(1), (2)同样适用。
(1) 生物地球化学模型
最简单的关于AOM反应的表述是双分子动力学方程[17]。如下:
$$ {R_{AOM}} = k \cdot \left[ {C{H_4}} \right] \cdot \left[ {SO_4^{2 - }} \right] $$ 由于对微生物调节的AOM反应机理的进一步认识,这种模型也在不断修正。如果充分考虑反应过程中的酶限制,那么双分子动力模型可以写成如下方程:
$$ \begin{array}{l} {R_{AOM}} = {v_{\max }} \cdot \left( {\frac{{\left[ {C{H_4}} \right]}}{{K_m^{C{H_4}} + \left[ {C{H_4}} \right]}}} \right) \cdot \\ \left( {\frac{{\left[ {SO_4^{2 - }} \right]}}{{K_m^{SO_4^{2 - }} + \left[ {SO_4^{2 - }} \right]}}} \right) \end{array} $$ 实验研究证明孔隙水中甲烷和硫酸盐含量会分别远小于其对应的半饱和常数,同时甲烷的半饱和常数要远大于硫酸根的半饱和常数,因此甲烷和硫酸根的米氏项就线性近似为依赖甲烷和硫酸根溶度的一次函数[74, 75]。所以:
$$ k = \frac{{{v_{\max }}}}{{K_m^{C{H_4}} \cdot K_m^{SO_4^{2 - }}}} $$ 通过催化AOM的反应,细胞内合成的ATP促使了微生物的代谢和生长。但是微生物得以生长的前提是反应产生的能量至少要超过最小代谢的阈值。如果考虑生物能量限制,这种模型就演变成:
$$ \begin{array}{l} {R_{AOM}} = {v_{\max }} \cdot \left( {\frac{{\left[ {C{H_4}} \right]}}{{K_m^{C{H_4}} + \left[ {C{H_4}} \right]}}} \right) \cdot \\ \left( {\frac{{\left[ {SO_4^{2 - }} \right]}}{{K_m^{SO_4^{2 - }} + \left[ {SO_4^{2 - }} \right]}}} \right) \cdot \left( {1 - \exp \left( {\frac{{\Delta {G_r} + \Delta {G_{ATP}}}}{{\chi RT}}} \right)} \right) \end{array} $$ (14) 通过简化成动力和热力驱动力,可以得到:
$$ {R_{AOM}} = {v_{\max }}{F_K}{F_T} $$ 式14中χ代表反应中穿过细胞膜的质子数,同时也表示每个反应方程式中体现的电子转移个数[76]。式14中吉布斯能计算如下:
$$ \Delta {G_r} = \Delta G_r^0 + RT\ln \frac{{{a_{H{S^ - }}} \cdot {a_{HCO_3^ - }} \cdot {a_{{H_2}O}}}}{{{a_{C{H_4}}} \cdot {a_{SO_4^{2 - }}}}} $$ a代表各种离子的活度, 上式中ΔGr+ΔGATP必须是负值才能使得整个反应得以进行。所以可以看出反应产物的累积会对反应的吉布斯自由能产生影响,从而影响到热力-动力模型中的RAOM值。
微生物调控下的AOM反应能否进行,取决于反应释放的吉布斯自由能是否大于生物的能量限制[23, 77, 78]。实验室中通过对大肠杆菌的实验测得生物的能量限制为15~20 kJ每摩尔电子供体,但是在不同的环境下测得不同的能量限制[79-81]。目前研究中常以Skaggerak中拟合得到的11 kJ作为ΔGATP值[76]。即使ΔGBQ是个常数,由于ΔGr在不同的条件下能量释放也不一样,所以反应速率也会不同。尤其是在SMTZ上部,由于甲烷的含量急剧降低,导致ΔGr较小,于是ATP数量也会较小[76]。当ATP能量不足以抵消ΔGATP时,硫酸盐氧化甲烷的反应就终止[76, 82-85]。
(2) 代谢模型
目前为止,还不能在实验室培养单一纯微生物,并使其催化AOM反应[86]。但目前研究报道中普遍认为AOM反应是由甲烷氧化古菌和硫酸盐还原细菌共同调节的氧化还原反应[87-89]。它们认为两种微生物之间的中间物质为氢气,甲酸和乙酸[90]。其中就以氢气为中间物质的反应为例,如下:
$$ {\rm{C}}{{\rm{H}}_4} + 3{{\rm{H}}_2}{\rm{O}} \to 4{{\rm{H}}_2} + {\rm{HCO}}_3^ - + {{\rm{H}}^ + } $$ $$ {\rm{SO}}_4^{2 - } + 4{{\rm{H}}_2} + {{\rm{H}}^ + } \to {\rm{H}}{{\rm{S}}^ - } + 4{{\rm{H}}_2}{\rm{O}} $$ 假设两种细菌以同心层状分布,由此得到的反应动力方程为:
$$ R = {B_{Arch}}{\rho _{Arch}} \times {\mathit{\Phi }_{MO}} \times {A^{MO}} $$ (15) 式(15)代表古菌甲烷缺氧氧化的速率。ρ代表单位体积中细胞个数,A代表假一级速率常数,而Φ代表的是一个连续函数。该函数表示为:
$$ {\mathit{\Phi }_{MO}} = \left\{ {\begin{array}{*{20}{l}} 1&{if\left[ {{H_2}} \right] < \left[ {{H_2}} \right]_{MO}^*}\\ 0&{if\left[ {{H_2}} \right] > \left[ {{H_2}} \right]_{MO}^*} \end{array}} \right. $$ 上式中的[ H2]MO*和[ H2]SRB*代表的在标准状态下甲烷缺氧氧化和硫酸盐还原作用释放能量等于ΔGATP时的氢气的浓度。
通过运用反应输运模型可以间接求得氢气的含量,这有助于对整个模型机制更深入认识[24, 91]。从而可以确定在甲烷缺氧氧化过程中的中间产物类型。
(3) 生物质-显式模型
氧化还原反应所产生的能量会成为微生物重要的能量来源,微生物利用这些能量合成新的细胞组织,因此甲烷缺氧氧化反应与生物体的生长具有一定联系[92]。由于对生存条件和对底物的竞争,不同的微生物可以形成不同的模型[93]。目前的模型是把微生物数量与底物利用相联系,描述如下:
$$ \begin{array}{l} \frac{{{\rm{d}}B}}{{{\rm{dt}}}} = Y \cdot \left( {\frac{{\left[ {C{H_4}} \right]}}{{K_m^{C{H_4}} + \left[ {C{H_4}} \right]}}} \right) \cdot \\ \left( {1 - \exp \left( {\frac{{\Delta {G_r} + \Delta {G_{ATP}}}}{{\chi RT}}} \right)} \right) - {\mu _{dec}} \cdot B \end{array} $$ (16) 式16中采用的是氢气为中间产物的代谢形式。然而在沉积物中微生物的代谢方式是多样的,需要找到一个对所有代谢途径都适用的表达式。μdec代表的是生物死亡,分解和排泄代谢废物,通过数据拟合得到的μdec值大约为0.1/a[53]。Y值大小取决于代谢反应的吉布斯能、合成有机质的吉布斯能和有机质利用能量的效率[94]。通过理论计算和实验得知Y值一般为每摩尔甲烷被氧化产生0.05~0.07摩尔生物质碳, 而相关微生物分裂一次的时间往往要几个月或几年,所以在后期短时间尺度模拟还是需要考虑微生物的情况[53, 95]。
2.2.3 模型适用性
上述的所有AOM反应模型中,双分子动力模型因其简单且需要测定的参数少而得到广泛运用,而其他模型都会有些缺陷。尽管实验证明,AOM反应首先受到甲烷限制,然而现实海底环境中并不能够判断反应受到哪种物质限制。深度较浅地区由于能量较为充足导致双分子动力学模型中热力项很少被提及。另外,代谢模型中由于缺乏中间物质的分布数据,模型应用受到一定程度的限制。而显示生物质模型由于不能够迅速反映环境的变化导致其不能普遍运用[96]。因此, 在不同的条件下,要采用不同的AOM模型,即使采用同种模型参数也是不尽相同。
3. 甲烷气相输运
热解气和水合物快速分解的气体易于通过气相超压破裂沉积层,从而喷出沉积物-海水界面[73, 97]。如果甲烷气泡被石油和水合物包裹,或者渗漏点水深小于1 500 m,这些甲烷气泡通常能溢出到大气中。但是由于AOM作用消耗溶解态甲烷,很多甲烷气泡会重新溶解在水体中。
如果溶解甲烷溶度超过了平衡时孔隙水中的甲烷溶解度,气泡产生速度公式如下:
$$ {R_{GF}} = {k_{GF}}\left( {{\rm{C}}{{\rm{H}}_{4\left( {{\rm{aq}}} \right)}}, - {\rm{CH}}_4^*} \right) $$ (17) 其中kGF是一级速率常数;而CH4*代表不同温度,压力和盐度下所决定的甲烷平衡溶度,计算方法如下[98]:
$$ \begin{array}{l} {\rm{CH}}_4^* = 1.4388 \times {10^{ - 7}}STP - 4.412 \times {10^{ - 5}}TP - \\ 4.6842 \times {10^{ - 5}}SP + 4.129 \times {10^{ - 9}}ST + 1.43465 \times \\ {10^{ - 2}}P - 1.6027 \times {10^{ - 6}}T - 1.2676 \times {10^{ - 6}}S + 4.9581\\ \times {10^{ - 4}} \end{array} $$ 产生的甲烷气泡不断向上迁移,并通过泥火山或麻坑向海水中溢出。目前对于气泡溢出,Haeckel提出了管状模型来描述上述过程[73]。这种模型主要将输运过程视为假扩散过程,并通过拟合获得扩散系数Keddy[96, 99]。首先要通过声波信息获得气泡的几何参数,然后根据下面的理论公式获得气泡上升速度:
$$ {u_{rise}} = 0.464\sqrt {g \cdot {r_{bubble}}} $$ 通常湍流中的扩散系数会正比于波速与长度的乘积,如果简化其比例系数为1,则原式为:
$$ {K_{eddy}} \approx {u_{rise}} \cdot {d_{bubble}} = 0.928\sqrt {g \cdot r_{bubble}^3} $$ 由于扩散系数随着时间和深度变化,如果其服从高斯分布:
$$ {K_{eddy}} = {K_0}{e^{ - {{\left( {\frac{{x - {u_{rise}}t}}{\sigma }} \right)}^2}}} $$ K0是指扩散常数,σ是指泡体之间的宽度。然后通过对上式求平均数得到:
$$ \left[ {{K_{eddy}}} \right] = \frac{{\iint {{K_{eddy}}}{\text{d}}x{\text{d}}t}}{{\iint {\text{d}}x{\text{d}}t}} $$ 于是:
$$ \left[ {{K_{eddy}}} \right] \approx {u_{rise}} \cdot {d_{bubble}} = d_{bubble}^2\frac{{{n_{bubble}}}}{{{t_{rise}}}} $$ 通过获得海底释放甲烷气泡的频率(fbubble),从而获得上升的甲烷气体通量:
$$ {F_{C{H_4}}} = {f_{bubble}} \cdot {V_{bubble}} = \frac{{\left[ {{K_{eddy}}} \right]}}{{4r_{bubble}^2}}{V_{bubble}} $$ 上述方法是由气泡灌洗作用而提出来一种模型。除此之外,有些学者也通过多相流达西定律对气体通量进行计算,获得了不错的结果[100]。而目前普遍的方法是甲烷气体的原位测量。为了能够准确得到甲烷从冷泉中释放到海水中的量,通常会结合水声探测仪器或水下摄影原位测量其通量[101-103]。
4. 展望
虽然在过去的30年中,对于表层碳周转的反应运输模型发展非常快,但是仍然使用的是不同程度的简化模型。这种简化模型在不同时空特征环境中参数都会不同,所以模型的适用范围也很有限。未来亟待发展一种能够在海底不同边界条件下适用的生物地球化学反应模型。在这里列出几个在未来模型研究中我们将要注意的几个重要问题。
有机质的降解性差异需要更多的对比性研究。如通过运用同一种模型对不同的底栖环境进行模拟,再与实验模拟数据对比得到不同地区有机质降解的重要影响因素。只有通过对有机质降解机制深一步的理解。才有可能用这种模型来模拟过去和未来。
对于AOM反应的限制因素中,目前对于维持生命的最小能量限制和反应过程中的中间产物还没有被确定,所以以后还需要大量工作来解决这些问题。而甲烷三种相态相互转化对于AOM反应速率也有影响,未来也应该考虑到反应速率模型中。
在甲烷溢出通量的计算方法中需要更充分的结合水下声学和光学设备,并建立合适的甲烷气泡溢出通量计算方法。
附表:模型术语表Appendix 1:Terminology in the models参数 定义 量纲反应输运模型 Z 沉积物深度 cm t 时间 yr C 浓度 mM G 有机质 wt-% φ 孔隙度因素 % Ds 多孔介质中物质扩散系数 cm2/a α 生物灌洗参数 /a vp 流体流动速率 cm/a vs 沉积物沉积速率 cm/a 早期成岩过程 vmax 最大反应速度 wt-%/a k 反应速率常数 /a Km, G 酶催化有机质降解半饱和常数 % i 种类 - j 反应序数 - Km, TEA 电子受体降解有机质半饱和常数 mM TEA 电子受体浓度 mM Kin 电子受体间抑制常数 mM ΔGr 反应标准吉布斯自由能 J/mol ΔGATP 合成
ATP最小能量J/mol mi 反应产生
ATP数- χ 反应平均化学计量数 - Ea 反应活化能 J/mol B 生物质含量 wt-% Y 微生物最大生长速度 - μdec 最大分解速度 /a RTEA 有机质的氧化还原速率 mol/a a 有机质初始年龄 k/a v 有机质分布 - 甲烷缺氧
氧化过程参数 定义 量纲 溶质溶度 mM χ 反应通过细胞膜的质子数 - a 离子活度 mM ρ 单位体积中细胞个数 m3 A 假一级速率常数 /a Φ 连续函数 - 甲烷气相输运 kGF 气泡形成速率常数 /a rbubble 气泡半径 cm K0 扩散常数 cm2/a σ 气泡之间的宽度 cm fbubble 气泡释放频率 s 致谢: 感谢两位审稿人仔细的阅读及提出的详细修改意见。 -
图 2 有机质降解和甲烷缺氧氧化概念图
(中间部分指按吉布斯自由能由大到小的氧化还原分区;虚线指甲烷渗漏,甲烷渗漏越强烈,硫酸盐甲烷转换带越靠近海底;而左边的有机质硫酸盐还原界面位置更深[17, 25])
Figure 2. Schematic graph of organic matter degradation and methane anaerobic oxidation
(Middle panel delineates several redox zone in the order of Gibbs energetic potential; dotted point indicates seepage of methane.The faster methane seeps, the sulfate-methane transition zone(shaded area at either side) will be closer to seafloor.Yet in the left panel, sulfate-methane transition zone in non-seep zone usually located deeper than seep area)
附表:模型术语表
Appendix 1:Terminology in the models
参数 定义 量纲反应输运模型 Z 沉积物深度 cm t 时间 yr C 浓度 mM G 有机质 wt-% φ 孔隙度因素 % Ds 多孔介质中物质扩散系数 cm2/a α 生物灌洗参数 /a vp 流体流动速率 cm/a vs 沉积物沉积速率 cm/a 早期成岩过程 vmax 最大反应速度 wt-%/a k 反应速率常数 /a Km, G 酶催化有机质降解半饱和常数 % i 种类 - j 反应序数 - Km, TEA 电子受体降解有机质半饱和常数 mM TEA 电子受体浓度 mM Kin 电子受体间抑制常数 mM ΔGr 反应标准吉布斯自由能 J/mol ΔGATP 合成
ATP最小能量J/mol mi 反应产生
ATP数- χ 反应平均化学计量数 - Ea 反应活化能 J/mol B 生物质含量 wt-% Y 微生物最大生长速度 - μdec 最大分解速度 /a RTEA 有机质的氧化还原速率 mol/a a 有机质初始年龄 k/a v 有机质分布 - 甲烷缺氧
氧化过程参数 定义 量纲 溶质溶度 mM χ 反应通过细胞膜的质子数 - a 离子活度 mM ρ 单位体积中细胞个数 m3 A 假一级速率常数 /a Φ 连续函数 - 甲烷气相输运 kGF 气泡形成速率常数 /a rbubble 气泡半径 cm K0 扩散常数 cm2/a σ 气泡之间的宽度 cm fbubble 气泡释放频率 s -
[1] Hazen R M, Schiffries C M. Why deep carbon[J]. Reviews in Mineralogy and Geochemistry, 2013, 75(1): 1-6. doi: 10.2138/rmg.2013.75.1
[2] IPCC. Climate Change 2013: the Physical Science Basis[M]//Stocker T F, Qin D, Plattner G K, et al. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom, New York, NY, USA: Cambridge University Press, 2013.
[3] Falkowski P, Scholes R J, Boyle E, et al. The global carbon cycle: a test of our knowledge of earth as a system[J]. Science, 2000, 290(5490): 291-296. doi: 10.1126/science.290.5490.291
[4] Jahnke R A. The global ocean flux of particulate organic carbon: Areal distribution and magnitude[J]. Global Biogeochemical Cycles, 1996, 10(1): 71-88. doi: 10.1029/95GB03525
[5] 曲建升, 孙成权, 张志强, 等.全球变化科学中的碳循环研究进展与趋向[J].地球科学进展, 2003, 18(6): 980-987. doi: 10.3321/j.issn:1001-8166.2003.06.021 QU Jiansheng, SUN Chengquan, ZHANG Zhiqiang, et al. Trends and advances of the global change studies on carbon cycle[J]. Advance in Earth Sciences, 2003, 18(6): 980-987. doi: 10.3321/j.issn:1001-8166.2003.06.021
[6] Berner R A, Canfield D E. A new model for atmospheric oxygen over phanerozoic time[J]. American Journal of Science, 1989, 289(4): 333-361. doi: 10.2475/ajs.289.4.333
[7] Wallmann K, Pinero E, Burwicz E, et al. The global inventory of methane hydrate in marine sediments: a theoretical approach[J]. Energies, 2012, 5(12): 2449-2498. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_4601df8c9815267b4a4ed024e0584614
[8] Dickens G R. Rethinking the global carbon cycle with a large, dynamic and microbially mediated gas hydrate capacitor[J]. Earth and Planetary Science Letters, 2003, 213(3-4): 169-183. doi: 10.1016/S0012-821X(03)00325-X
[9] Boetius A, Ravenschlag K, Schubert C J, et al. Marine microbial consortium apparently mediating anaerobic oxidation of methane[J]. Nature, 2000, 407(6804): 623-626. doi: 10.1038/35036572
[10] Reeburgh W S. Oceanic methane biogeochemistry[J]. Chemical Reviews, 2007, 107(2): 486-513. doi: 10.1021/cr050362v
[11] Schulz H D, Zabel M. Marine Geochemistry[M]. 2nd ed. Berlin Heidelberg: Springer, 2006.
[12] 陈多福, 陈先沛, 陈光谦.冷泉流体沉积碳酸盐岩的地质地球化学特征[J].沉积学报, 2002, 20(1): 34-40. doi: 10.3969/j.issn.1000-0550.2002.01.007 CHEN Duofu, CHEN Xianpei, CHEN Guangqian. Geology and geochemistry of cold seepage and venting-related carbonates[J]. Acta Sedimentologica Sinica, 2002, 20(1): 34-40. doi: 10.3969/j.issn.1000-0550.2002.01.007
[13] Niemann H, Losekann T, de Beer D, et al. Novel microbial communities of the haakon mosby mud volcano and their role as a methane sink[J]. Nature, 2006, 443(7113): 854-858. doi: 10.1038/nature05227
[14] Sommer S, Pfannkuche O, Linke P, et al. Efficiency of the benthic filter: biological control of the emission of dissolved methane from sediments containing shallow gas hydrates at hydrate ridge[J]. Global Biogeochemical Cycles, 2006, 20(2): GB2019.
[15] Burdige D J. Preservation of organic matter in marine sediments: controls, mechanisms, and an imbalance in sediment organic carbon budgets?[J]. Chemical Reviews, 2007, 107(2): 467-485. doi: 10.1021/cr050347q
[16] Hedges J I, Keil R G. Sedimentary organic matter preservation: an assessment and speculative synthesis[J]. Marine Chemistry, 1995, 49(2-3): 81-115. doi: 10.1016/0304-4203(95)00008-F
[17] Regnier P, Dale A W, Arndt S, et al. Quantitative analysis of anaerobic oxidation of methane (AOM) in marine sediments: a modeling perspective[J]. Earth-Science Reviews, 2011, 106(1-2): 105-130. doi: 10.1016/j.earscirev.2011.01.002
[18] Boetius A, Wenzhöfer F. Seafloor oxygen consumption fuelled by methane from cold seeps[J]. Nature Geoscience, 2013, 6(9): 725-734. doi: 10.1038/ngeo1926
[19] Berner R A. Early Diagenesis: A Theoretical Approach[M]. Princeton: Princeton University Press, 1980: 1-224.
[20] Boudreau B P. Diagenetic Models and Their Implementation[M]. Berlin Heidelberg: Springer, 1997.
[21] Chuang P C, Dale A W, Wallmann K, et al. Relating sulfate and methane dynamics to geology: accretionary prism offshore SW Taiwan[J]. Geochemistry, Geophysics, Geosystems, 2013, 14(7): 2523-2545. doi: 10.1002/ggge.20168
[22] Middelburg J J. A simple rate model for organic matter decomposition in marine sediments[J]. Geochimica et Cosmochimica Acta, 1989, 53(7): 1577-1581. doi: 10.1016/0016-7037(89)90239-1
[23] Hoehler T M, Alperin M J, Albert D B, et al. Field and laboratory studies of methane oxidation in an anoxic marine sediment: evidence for a methanogen-sulfate reducer consortium[J]. Global Biogeochemical Cycles, 1994, 8(4): 451-463. doi: 10.1029/94GB01800
[24] Alperin M J, Hoehler T M. Anaerobic methane oxidation by archaea/sulfate-reducing bacteria aggregates: 1. Thermodynamic and physical constraints[J]. American Journal of Science, 2009, 309(10): 869-957. doi: 10.2475/10.2009.01
[25] Glud R N. Oxygen dynamics of marine sediments[J]. Marine Biology Research, 2008, 4(4): 243-289. doi: 10.1080/17451000801888726
[26] Seiter K, Hensen C, Schröter J, et al. Organic carbon content in surface sediments-defining regional provinces[J]. Deep Sea Research Part I: Oceanographic Research Papers, 2004, 51(12): 2001-2026. doi: 10.1016/j.dsr.2004.06.014
[27] Hedges J I, Keil R G. Sedimentary organic matter preservation: an assessment and speculative synthesis[J]. Marine Chemistry, 1995, 49(2-3): 81-115. doi: 10.1016/0304-4203(95)00008-F
[28] Jorgensen B B, Boetius A. Feast and famine-microbial life in the deep-sea bed[J]. Nature Reviews Microbiology, 2007, 5(10): 770-781. doi: 10.1038/nrmicro1745
[29] Claypool G E, Milkov A V, Lee Y J, et al. Microbial methane generation and gas transport in shallow sediments of an accretionary complex, southern hydrate ridge (ODP leg 204), Offshore Oregon, USA[C]//Tréhu A M, Bohrmann G, Torres M E, et al. Proceedings of the Ocean Drilling Program, Scentific Results. College Station, TX: Ocean Drilling Program, 2006: 1-52.
[30] Røy H, Kallmeyer J, Adhikari R R, et al. Aerobic microbial respiration in 86-million-year-old deep-sea red clay[J]. Science, 2012, 336(6083): 922-925. doi: 10.1126/science.1219424
[31] Mayer L M. Extent of coverage of mineral surfaces by organic matter in marine sediments[J]. Geochimica et Cosmochimica Acta, 1999, 63(2): 207-215. doi: 10.1016/S0016-7037(99)00028-9
[32] Blair N E, Aller R C. The fate of terrestrial organic carbon in the marine environment[J]. Annual Review of Marine Science, 2012, 4(1): 401-423. doi: 10.1146/annurev-marine-120709-142717
[33] Arndt S, Jørgensen B B, LaRowe D E, et al. Quantifying the degradation of organic matter in marine sediments: a review and synthesis[J]. Earth-Science Reviews, 2013, 123: 53-86. doi: 10.1016/j.earscirev.2013.02.008
[34] Middelburg J J. Chemoautotrophy in the ocean[J]. Geophysical Research Letters, 2011, 38(24): L24604. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_03e91f27b4245dd821be9b8c6fb137ca
[35] Wilson J D, Barker S, Ridgwell A. Assessment of the spatial variability in particulate organic matter and mineral sinking fluxes in the ocean interior: implications for the ballast hypothesis[J]. Global Biogeochemical Cycles, 2012, 26(4): GB4011. http://cn.bing.com/academic/profile?id=42d9bb4613e13785f635178d8f7b568b&encoded=0&v=paper_preview&mkt=zh-cn
[36] Henson S A, Sanders R, Madsen E. Global patterns in efficiency of particulate organic carbon export and transfer to the deep ocean[J]. Global Biogeochemical Cycles, 2012, 26(1): GB1028. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1029/2011GB004099
[37] Francois R, Honjo S, Krishfield R, et al. Factors controlling the flux of organic carbon to the bathypelagic zone of the ocean[J]. Global Biogeochemical Cycles, 2002, 16(4): 34-1-34-20. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1029/2001GB001722
[38] Hatakka A. Lignin-modifying enzymes from selected white-rot fungi: production and role in lignin degradation[J]. FEMS Microbiology Reviews, 1994, 13(2-3): 125-135. doi: 10.1111/j.1574-6976.1994.tb00039.x
[39] Schippers A, Köweker G, Höft C, et al. Quantification of microbial communities in forearc sediment basins off sumatra[J]. Geomicrobiology Journal, 2010, 27(2): 170-182. doi: 10.1080/01490450903456798
[40] Lipp J S, Morono Y, Inagaki F, et al. Significant contribution of archaea to extant biomass in marine subsurface sediments[J]. Nature, 2008, 454(7207): 991-994. doi: 10.1038/nature07174
[41] Biddle J F, Lipp J S, Lever M A, et al. Heterotrophic archaea dominate sedimentary subsurface ecosystems off peru[J]. Proceedings of the National Academy of Sciences of the United States of America, 2006, 103(10): 3846-3851. doi: 10.1073/pnas.0600035103
[42] LaRowe D E, Van Cappellen P. Degradation of natural organic matter: a thermodynamic analysis[J]. Geochimica et Cosmochimica Acta, 2011, 75(8): 2030-2042. doi: 10.1016/j.gca.2011.01.020
[43] Bethke C M, Sanford R A, Kirk M F, et al. The thermodynamic ladder in geomicrobiology[J]. American Journal of Science, 2011, 311(3): 183-210. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=8f36502629bc9fa067b4db5e9b0fcdc5
[44] Finke N, Jorgensen B B. Response of fermentation and sulfate reduction to experimental temperature changes in temperate and arctic marine sediments[J]. The ISME Journal, 2008, 2(8): 815-829. doi: 10.1038/ismej.2008.20
[45] von Lützow M, Kögel-Knabner I. Temperature sensitivity of soil organic matter decomposition-what do we know?[J]. Biology and Fertility of Soils, 2009, 46(1): 1-15. doi: 10.1007/s00374-009-0413-8
[46] Robador A, Brüchert V, Steen A D, et al. Temperature induced decoupling of enzymatic hydrolysis and carbon remineralization in long-term incubations of arctic and temperate sediments[J]. Geochimica et Cosmochimica Acta, 2010, 74(8): 2316-2326. doi: 10.1016/j.gca.2010.01.022
[47] Robador A, Brüchert V, Jorgensen B B. The impact of temperature change on the activity and community composition of sulfate-reducing bacteria in arctic versus temperate marine sediments[J]. Environmental Microbiology, 2009, 11(7): 1692-1703. doi: 10.1111/j.1462-2920.2009.01896.x
[48] Hubert C, Loy A, Nickel M, et al. A constant flux of diverse thermophilic bacteria into the cold arctic seabed[J]. Science, 2009, 325(5947): 1541-1544. doi: 10.1126/science.1174012
[49] Hubert C, Arnosti C, Brüchert V, et al. Thermophilic anaerobes in arctic marine sediments induced to mineralize complex organic matter at high temperature[J]. Environmental Microbiology, 2010, 12(4): 1089-1104. doi: 10.1111/j.1462-2920.2010.02161.x
[50] Lalonde k, Mucci A, Ouellet A, et al. Preservation of organic matter in sediments promoted by iron[J]. Nature, 2012, 483(7388): 198-200. doi: 10.1038/nature10855
[51] Kristensen E, Hansen T, Delefosse M, et al. Contrasting effects of the polychaetes Marenzelleria viridis and Nereis diversicolor on benthic metabolism and solute transport in sandy coastal sediment[J]. Marine Ecology Progress Series, 2011, 425: 125-139. doi: 10.3354/meps09007
[52] Thullner M, Regnier P, Van Cappellen P. Modeling microbially induced carbon degradation in redox-stratified subsurface environments: concepts and open questions[J]. Geobiology Journal, 2007, 24(3-4): 139-155. http://cn.bing.com/academic/profile?id=84f658ac61a8d7ffe3cffc37ce206afe&encoded=0&v=paper_preview&mkt=zh-cn
[53] Dale A W, Regnier P, Van Cappellen P. Bioenergetic controls on anaerobic oxidation of methane(AOM) in coastal marine sediments: a theoretical analysis[J]. American Journal of Science, 2006, 306(4): 246-294. doi: 10.2475/ajs.306.4.246
[54] Dale A W, Van Cappellen P, Aguilera D R, et al. Methane efflux from marine sediments in passive and active margins: estimations from bioenergetic reaction-transport simulations[J]. Earth and Planetary Science Letters, 2008, 265(3-4): 329-344. doi: 10.1016/j.epsl.2007.09.026
[55] Jorgensen B B. A comparison of methods for the quantification of bacterial sulfate reduction in coastal marine sediments[J]. Geomicrobiology Journal, 1978, 1(1): 29-47. doi: 10.1080/01490457809377722
[56] Boudreau B P, Ruddick B R. On a reactive continuum representation of organic matter diagenesis[J]. American Journal of Science, 1991, 291(5): 507-538. doi: 10.2475/ajs.291.5.507
[57] Tarutis Jr W J. On the equivalence of the power and reactive continuum models of organic matter diagenesis[J]. Geochimica et Cosmochimica Acta, 1993, 57(6): 1349-1350. doi: 10.1016/0016-7037(93)90071-4
[58] Wallmann K, Aloisi G, Haeckel M, et al. Kinetics of organic matter degradation, microbial methane generation, and gas hydrate formation in anoxic marine sediments[J]. Geochimica et Cosmochimica Acta, 2006, 70(15): 3905-3927. doi: 10.1016/j.gca.2006.06.003
[59] Arndt S, Brumsack H J, Wirtz K W. Cretaceous black shales as active bioreactors: a biogeochemical model for the deep biosphere encountered during ODP Leg 207 (Demerara Rise)[J]. Geochimica et Cosmochimica Acta, 2006, 70(2): 408-425. doi: 10.1016/j.gca.2005.09.010
[60] Wadham J L, Arndt S, Tulaczyk S, et al. Potential methane reservoirs beneath antarctica[J]. Nature, 2012, 488(7413): 633-637. doi: 10.1038/nature11374
[61] Arndt S, Hetzel A, Brumsack H J. Evolution of organic matter degradation in cretaceous black shales inferred from authigenic barite: a reaction-transport model[J]. Geochimica et Cosmochimica Acta, 2009, 73(7): 2000-2022. doi: 10.1016/j.gca.2009.01.018
[62] Wehrmann L M, Arndt S, März C, et al. The evolution of early diagenetic signals in bering sea subseafloor sediments in response to varying organic carbon deposition over the last 4.3 Ma[J]. Geochimica et Cosmochimica Acta, 2013, 109: 175-196. doi: 10.1016/j.gca.2013.01.025
[63] Buffett B, Archer D. Global inventory of methane clathrate: sensitivity to changes in the deep ocean[J]. Earth and Planetary Science Letters, 2004, 227(3-4): 185-199. doi: 10.1016/j.epsl.2004.09.005
[64] Beaudoin Y C, Waite W F, Boswell R, et al. Frozen heat: a UNEP global outlook on methane gas hydrates[R]. GRID-Arendal, Norway: United Nations Environment Programme, 2014.
[65] Borowski W S, Paull C K, Ussler W. Marine pore-water sulfate profiles indicate in situ methane flux from underlying gas hydrate[J]. Geology, 1996, 24(7): 655-658. doi: 10.1130/0091-7613(1996)024<0655:MPWSPI>2.3.CO;2
[66] Milucka J, Ferdelman T G, Polerecky L, et al. Zero-valent sulphur is a key intermediate in marine methane oxidation[J]. Nature, 2012, 491(7425): 541-546. doi: 10.1038/nature11656
[67] Borowski W S, Paull C K, Ussler Ⅲ W. Global and local variations of interstitial sulfate gradients in deep-water, continental margin sediments: sensitivity to underlying methane and gas hydrates[J]. Marine Geology, 1999, 159(1-4): 131-154. doi: 10.1016/S0025-3227(99)00004-3
[68] Jensen M M, Holmer M, Thamdrup B. Composition and diagenesis of neutral carbohydrates in sediments of the baltic-north sea transition[J]. Geochimica et Cosmochimica Acta, 2005, 69(16): 4085-4099. doi: 10.1016/j.gca.2005.01.021
[69] Burdige D J, Skoog A, Gardner K. Dissolved and particulate carbohydrates in contrasting marine sediments[J]. Geochimica et Cosmochimica Acta, 2000, 64(6): 1029-1041. doi: 10.1016/S0016-7037(99)00361-0
[70] Jørgensen B B, Nelson D C. Sulfide oxidation in marine sediments: geochemistry meets microbiology[J]. Geological Society of America Special Papers, 2004, 379: 63-81. http://cn.bing.com/academic/profile?id=e0da9bc5b969558a176fc8dd0c323e06&encoded=0&v=paper_preview&mkt=zh-cn
[71] Emeis K C, Brüchert V, Currie B, et al. Shallow gas in shelf sediments of the namibian coastal upwelling ecosystem[J]. Continental Shelf Research, 2004, 24(6): 627-642. doi: 10.1016/j.csr.2004.01.007
[72] Hensen C, Wallmann K. Methane formation at Costa Rica continental margin-constraints for gas hydrate inventories and cross-décollement fluid flow[J]. Earth and Planetary Science Letters, 2005, 236(1-2): 41-60. doi: 10.1016/j.epsl.2005.06.007
[73] Haeckel M, Boudreau B P, Wallmann K. Bubble-induced porewater mixing: a 3-D model for deep porewater irrigation[J]. Geochimica et Cosmochimica Acta, 2007, 71(21): 5135-5154. doi: 10.1016/j.gca.2007.08.011
[74] Wegener G, Boetius A. An experimental study on short-term changes in the anaerobic oxidation of methane in response to varying methane and sulfate fluxes[J]. Biogeosciences, 2009, 6(5): 867-876. doi: 10.5194/bg-6-867-2009
[75] Nauhaus K, Boetius A, Krüger M, et al. In vitro demonstration of anaerobic oxidation of methane coupled to sulphate reduction in sediment from a marine gas hydrate area[J]. Environmental Microbiology, 2002, 4(5): 296-305. doi: 10.1046/j.1462-2920.2002.00299.x
[76] Dale A W, Regnier P, Knab N J, et al. Anaerobic oxidation of methane (AOM) in marine sediments from the skagerrak (Denmark): Ⅱ. Reaction-transport modeling[J]. Geochimica et Cosmochimica Acta, 2008, 72(12): 2880-2894. doi: 10.1016/j.gca.2007.11.039
[77] Larowe D E, Dale A W, Regnier P. A thermodynamic analysis of the anaerobic oxidation of methane in marine sediments[J]. Geobiology, 2008, 6(5): 436-449. doi: 10.1111/j.1472-4669.2008.00170.x
[78] Knab N J, Dale A W, Lettmann K, et al. Thermodynamic and kinetic control on anaerobic oxidation of methane in marine sediments[J]. Geochimica et Cosmochimica Acta, 2008, 72(15): 3746-3757. doi: 10.1016/j.gca.2008.05.039
[79] Schink B. Energetics of syntrophic cooperation in methanogenic degradation[J]. Microbiology and Molecular Biology Reviews, 1997, 61(2): 262-280. http://d.old.wanfangdata.com.cn/OAPaper/oai_pubmedcentral.nih.gov_232610
[80] Larowe D E, Helgeson H C. Quantifying the energetics of metabolic reactions in diverse biogeochemical systems: electron flow and atp synthesis[J]. Geobiology, 2007, 5(2): 153-168. doi: 10.1111/j.1472-4669.2007.00099.x
[81] Hoehler T M. Biological energy requirements as quantitative boundary conditions for life in the subsurface[J]. Geobiology, 2004, 2(4): 205-215. doi: 10.1111/j.1472-4677.2004.00033.x
[82] Knab N J, Cragg B A, Hornibrook E R C, et al. Regulation of anaerobic methane oxidation in sediments of the Black Sea[J]. Biogeosciences, 2009, 6(8): 1505-1518. doi: 10.5194/bg-6-1505-2009
[83] Treude T, Krüger M, Boetius A, et al. Environmental control on anaerobic oxidation of methane in the gassy sediments of Eckernforde bay (German baltic)[J]. Limnology and Oceanography, 2005, 50(6): 1771-1786. doi: 10.4319/lo.2005.50.6.1771
[84] Jorgensen B B, Weber A, Zopfi J. Sulfate reduction and anaerobic methane oxidation in Black Sea sediments[J]. Deep Sea Research Part I: Oceanographic Research Papers, 2001, 48(9): 2097-2120. doi: 10.1016/S0967-0637(01)00007-3
[85] Fossing H, Ferdelman T G, Berg P. Sulfate reduction and methane oxidation in continental margin sediments influenced by irrigation (South-East Atlantic off Namibia)[J]. Geochimica et Cosmochimica Acta, 2000, 64(5): 897-910. doi: 10.1016/S0016-7037(99)00349-X
[86] Knittel K, Boetius A. Anaerobic oxidation of methane: progress with an unknown process[J]. Annual Review of Microbiology, 2009, 63(1): 311-334. doi: 10.1146/annurev.micro.61.080706.093130
[87] Orphan V J, House C H, Hinrichs K U, et al. Multiple archaeal groups mediate methane oxidation in anoxic cold seep sediments[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(11): 7663-7668. doi: 10.1073/pnas.072210299
[88] Orphan V J, House C H, Hinrichs K U, et al. Methane-consuming archaea revealed by directly coupled isotopic and phylogenetic analysis[J]. Science, 2001, 293(5529): 484-487. doi: 10.1126/science.1061338
[89] Wefer G, Billett D, Hebbeln D, et al. Ocean Margin Systems[M]. Berlin Heidelberg: Springer, 2003.
[90] Nauhaus K, Treude T, Boetius A, et al. Environmental regulation of the anaerobic oxidation of methane: a comparison of anme-Ⅰand anme-Ⅱcommunities[J]. Environmental Microbiology, 2005, 7(1): 98-106. doi: 10.1111/j.1462-2920.2004.00669.x
[91] Orcutt B, Meile C. Constraints on mechanisms and rates of anaerobic oxidation of methane by microbial consortia: process-based modeling of ANME-2 archaea and sulfate reducing bacteria interactions[J]. Biogeosciences, 2008, 5(6): 1587-1599. doi: 10.5194/bg-5-1587-2008
[92] Rittmann B E, VanBriesen J M. Microbiological processes in reactive modeling[J]. Reviews in Mineralogy and Geochemistry, 1996, 34(1): 311-334. http://cn.bing.com/academic/profile?id=200ff7afe97b3965004add2bdc6b8d2a&encoded=0&v=paper_preview&mkt=zh-cn
[93] Thullner M, Van Cappellen P, Regnier P. Modeling the impact of microbial activity on redox dynamics in porous media[J]. Geochimica et Cosmochimica Acta, 2005, 69(21): 5005-5019. doi: 10.1016/j.gca.2005.04.026
[94] VanBriesen J M. Evaluation of methods to predict bacterial yield using thermodynamics[J]. Biodegradation, 2002, 13(3): 171-190. doi: 10.1023/A:1020887214879
[95] Nauhaus K, Albrecht M, Elvert M, et al. In vitro cell growth of marine archaeal-bacterial consortia during anaerobic oxidation of methane with sulfate[J]. Environmental Microbiology, 2007, 9(1): 187-196. doi: 10.1111/j.1462-2920.2006.01127.x
[96] Dale A W, Aguilera D R, Regnier P, et al. Seasonal dynamics of the depth and rate of anaerobic oxidation of methane in Aarhus bay (Denmark) sediments[J]. Journal of Marine Research, 2008, 66(1): 127-155. doi: 10.1357/002224008784815775
[97] Martens C S, Klump J V. Biogeochemical cycling in an organic-rich coastal marine basin-Ⅰ. Methane sediment-water exchange processes[J]. Geochimica et Cosmochimica Acta, 1980, 44(3): 471-490. doi: 10.1016/0016-7037(80)90045-9
[98] Duan Z H, Moller N, Greenberg J, et al. The prediction of methane solubility in natural waters to high ionic strength from 0 to 250℃ and from 0 to 1600 bar[J]. Geochimica et Cosmochimica Acta, 1992, 56(4): 1451-1460. doi: 10.1016/0016-7037(92)90215-5
[99] Dale A W, Regnier P, Van Cappellen P, et al. Remote quantification of methane fluxes in gassy marine sediments through seismic survey[J]. Geology, 2009, 37(3): 235-238. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a10a36b85a341ecd56c497b5e8871e4f
[100] Smith A J, Flemings P B, Fulton P M. Hydrocarbon flux from natural deepwater Gulf of Mexico vents[J]. Earth and Planetary Science Letters, 2014, 395: 241-253. doi: 10.1016/j.epsl.2014.03.055
[101] Römer M, Sahling H, Pape T, et al. Quantification of gas bubble emissions from submarine hydrocarbon seeps at the makran continental margin (offshore Pakistan)[J]. Journal of Geophysical Research: Oceans, 2012, 117(C10): C10015. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1029/2011JC007424
[102] Greinert J, Artemov Y, Egorov V, et al. 1300-m-high rising bubbles from mud volcanoes at 2080 m in the black sea: hydroacoustic characteristics and temporal variability[J]. Earth and Planetary Science Letters, 2006, 244(1-2): 1-15. doi: 10.1016/j.epsl.2006.02.011
[103] Greinert J, Lewis K B, Bialas J, et al. Methane seepage along the hikurangi margin, New Zealand: overview of studies in 2006 and 2007 and new evidence from visual, bathymetric and hydroacoustic investigations[J]. Marine Geology, 2010, 272(1-4): 6-25. doi: 10.1016/j.margeo.2010.01.017
-
期刊类型引用(1)
1. 刘超,李昕,梁天,刘萧萧,陈浩,安海花. 冷泉碳酸盐工厂的提出及古气候意义. 沉积学报. 2024(02): 387-402 .  百度学术
百度学术
其他类型引用(3)



 下载:
下载: